Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T07:30:07.298Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of turbulence characteristics in a temporal dense gas compressible mixing layer using direct numerical simulation

Published online by Cambridge University Press:  21 April 2020

Aurélien Vadrot Open the ORCID record for Aurélien Vadrot [Opens in a new window] ,
Alexis Giauque Open the ORCID record for Alexis Giauque [Opens in a new window]  and
Christophe Corre Open the ORCID record for Christophe Corre [Opens in a new window]
Aurélien Vadrot*
Affiliation:
LMFA – Laboratoire de Mécanique des Fluides et d’Acoustique, Ecole Centrale de Lyon, 36 avenue Guy de Collongue, 69134Ecully CEDEX, France
Alexis Giauque
Affiliation:
LMFA – Laboratoire de Mécanique des Fluides et d’Acoustique, Ecole Centrale de Lyon, 36 avenue Guy de Collongue, 69134Ecully CEDEX, France
Christophe Corre
Affiliation:
LMFA – Laboratoire de Mécanique des Fluides et d’Acoustique, Ecole Centrale de Lyon, 36 avenue Guy de Collongue, 69134Ecully CEDEX, France
*
†Email address for correspondence: aurelien.vadrot@ec-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

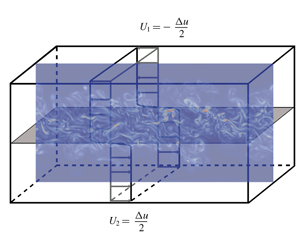
This study investigates the effects of a Bethe–Zel’dovich–Thompson (BZT) dense gas (FC-70) on the development of a turbulent compressible mixing layer at a convective Mach number $M_{c}=1.1$. Three-dimensional direct numerical simulations are performed with both FC-70 and air. The initial thermodynamic state for FC-70 lies inside the inversion region where the fundamental derivative of gas dynamics ($\unicode[STIX]{x1D6E4}$) becomes negative. The complex Martin–Hou thermodynamic equation of state is used to reproduce thermodynamic peculiarities of the BZT dense gas (DG). The unstable growth phase in the mixing layer development shows an increase of $xy$-turbulent stress tensors in DG compared to perfect gas (PG). The following self-similar period has been carefully defined from the time evolution of the integrated streamwise production and transport terms. During the self-similar stage, DG and PG mixing layers at $M_{c}=1.1$ display close values of the momentum thickness growth rate, which seems similarly affected by the well-known compressibility-related reduction for PG. The same mechanisms are at stake, related to the reduction of pressure–strain terms. Turbulent kinetic energy (TKE) spectra show a slower decrease of TKE at small scales for DG compared with PG. The filtered kinetic energy equation balance developed by Aluie (Physica D, vol. 247 (1), 2013, pp. 54–65) is applied for the first time to a compressible mixing layer. The equation is reshaped to better account for TKE transport across the mixing layer. This new formulation brings out the role played by $\unicode[STIX]{x1D6F4}_{l}$, the pressure strengths power. A detailed comparison of the contributions to the filtered TKE equation is provided for both PG and DG mixing layers.

JFM classification

Turbulent Flows: Compressible turbulence Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 893 , 25 June 2020 , A10
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almagro, A., García-Villalba, M. & Flores, O. 2017 A numerical study of a variable-density low-speed turbulent mixing layer. J. Fluid Mech. 830, 569–601.CrossRefGoogle Scholar
Aluie, H. 2013 Scale decomposition in compressible turbulence. Physica D 247 (1), 54–65.Google Scholar
Anders, J. B., Anderson, W. K. & Murthy, A. V. 1999 Transonic similarity theory applied to a supercritical airfoil in heavy gas. J. Aircraft 36 (6), 957–964.CrossRefGoogle Scholar
Argrow, B. M. 1996 Computational analysis of dense gas shock tube flow. Shock Waves 6 (4), 241–248.CrossRefGoogle Scholar
Bailly, C. & Comte-Bellot, G.2003 Turbulence. Sciences et techniques de l’ingénieur, CNRS Editions.Google Scholar
Barre, S. & Bonnet, J. P. 2015 Detailed experimental study of a highly compressible supersonic turbulent plane mixing layer and comparison with most recent DNS results: towards an accurate description of compressibility effects in supersonic free shear flows. Intl J. Heat Fluid Flow 51, 324–334.CrossRefGoogle Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Bethe, H. A.1942 The theory of shock waves for an arbitrary equation of state. Res. and Dev, Tech. Paper 545.Google Scholar
Bogdanoff, D. W. 1983 Compressibility effects in turbulent shear layers. AIAA J. 21 (6), 926–927.CrossRefGoogle Scholar
Borisov, A. A., Borisov, A. A., Kutateladze, S. S. & Nakoryakov, V. E. 1983 Rarefaction shock wave near the critical liquid–vapour point. J. Fluid Mech. 126, 59–73.CrossRefGoogle Scholar
Bradshaw, P. 1966 The effect of initial conditions on the development of a free shear layer. J. Fluid Mech. 26 (2), 225–236.CrossRefGoogle Scholar
Bradshaw, P. 1977 Compressible turbulent shear layers. Annu. Rev. Fluid Mech. 9 (1), 33–52.CrossRefGoogle Scholar
Breidenthal, R. E. 1992 Sonic eddy-a model for compressible turbulence. AIAA J. 30 (1), 101–104.CrossRefGoogle Scholar
Brown, B. P. & Argrow, B. M. 1998 Nonclassical dense gas flows for simple geometries. AIAA J. 36 (10), 1842–1847.CrossRefGoogle Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (4), 775–816.CrossRefGoogle Scholar
de Bruin, I.2001 Direct and large-eddy simulation of the spatial turbulent mixing layer. PhD thesis, Eindhoven University of Technology.Google Scholar
Cadieux, F., Domaradzki, J. A., Sayadi, T., Bose, T. & Duchaine, F. 2012 DNS and LES of separated flows at moderate Reynolds numbers. In Proceedings of the 2012 Summer Program, pp. 77–86. Center for Turbulence Research, NASA Ames/Stanford University.Google Scholar
Chung, T. H., Ajlan, M., Lee, L. L. & Starling, K. E. 1988 Generalized multiparameter correlation for nonpolar and polar fluid transport properties. Ind. Engng Chem. Res. 27 (4), 671–679.CrossRefGoogle Scholar
Cinnella, P. & Congedo, P. M. 2005 Aerodynamic performance of transonic Bethe–Zel’dovich–Thompson flows past an airfoil. AIAA J. 43 (2), 370–378.CrossRefGoogle Scholar
Cinnella, P. & Congedo, P. M. 2007 Inviscid and viscous aerodynamics of dense gases. J. Fluid Mech. 580, 179–217.CrossRefGoogle Scholar
Colin, O. & Rudgyard, M. 2000 Development of high-order Taylor–Galerkin schemes for LES. J. Comput. Phys. 162 (2), 338–371.CrossRefGoogle Scholar
Colonna, P. & Guardone, A. 2006 Molecular interpretation of nonclassical gas dynamics of dense vapors under the van der Waals model. Phys. Fluids 18 (5), 056101.CrossRefGoogle Scholar
Colonna, P., Guardone, A., Nannan, N. R. & Zamfirescu, C. 2008 Design of the dense gas flexible asymmetric shock tube. Trans. ASME J. Fluids Engng 130 (3), 034501.CrossRefGoogle Scholar
Colonna, P. & Rebay, S. 2004 Numerical simulation of dense gas flows on unstructured grids with an implicit high resolution upwind Euler solver. Intl J. Numer. Meth. Fluids 46 (7), 735–765.CrossRefGoogle Scholar
Congedo, P. M., Corre, C. & Cinnella, P. 2007 Airfoil shape optimization for transonic flows Bethe–Zel’dovich–Thompson fluids. AIAA J. 45 (6), 1303–1316.CrossRefGoogle Scholar
Congedo, P. M., Corre, C. & Cinnella, P. 2011 Numerical investigation of dense-gas effects in turbomachinery. Comput. Fluids 49 (1), 290–301.CrossRefGoogle Scholar
Costello, M. G., Flynn, R. M. & Owens, J. G.2000 Fluoroethers and fluoroamines. In Kirk–Othmer Encyclopedia of Chemical Technology. John Wiley & Sons.Google Scholar
Cramer, M. S. 1989 Negative nonlinearity in selected fluorocarbons. Phys. Fluids A 1 (11), 1894–1897.CrossRefGoogle Scholar
Cramer, M. S. 1991 Nonclassical dynamics of classical gases. In Nonlinear Waves in Real Fluids, pp. 91–145. Springer.CrossRefGoogle Scholar
Cramer, M. S. & Crickenberger, A. B. 1991 The dissipative structure of shock waves in dense gases. J. Fluid Mech. 223, 325–355.CrossRefGoogle Scholar
Cramer, M. S. & Kluwick, A. 1984 On the propagation of waves exhibiting both positive and negative nonlinearity. J. Fluid Mech. 142, 9–37.CrossRefGoogle Scholar
Cramer, M. S. & Park, S. 1999 On the suppression of shock-induced separation in Bethe–Zel’dovich–Thompson fluids. J. Fluid Mech. 393, 1–21.CrossRefGoogle Scholar
Cramer, M. S. & Sen, R. 1986 Shock formation in fluids having embedded regions of negative nonlinearity. Phys. Fluids 29 (7), 2181–2191.CrossRefGoogle Scholar
Dai, Q., Jin, T., Luo, K. & Fan, J. 2018 Direct numerical simulation of particle dispersion in a three-dimensional spatially developing compressible mixing layer. Phys. Fluids 30 (11), 113301.Google Scholar
Desoutter, G., Habchi, C., Cuenot, B. & Poinsot, T. 2009 DNS and modeling of the turbulent boundary layer over an evaporating liquid film. Intl J. Heat Mass Transfer 52 (25–26), 6028–6041.CrossRefGoogle Scholar
Dura Galiana, F. J., Wheeler, A. P. S. & Ong, J. 2016 A study of trailing-edge losses in organic rankine cycle turbines. J. Turbomach. 138 (12), 121003.CrossRefGoogle Scholar
Fergason, S. H. & Argrow, B. M. 2001 Simulations of nonclassical dense gas dynamics. In 35th AIAA Thermophysics Conference, Anaheim, CO.Google Scholar
Fergason, S. H., Ho, T. L., Argrow, B. M. & Emanuel, G. 2001 Theory for producing a single-phase rarefaction shock wave in a shock tube. J. Fluid Mech. 445, 37–54.CrossRefGoogle Scholar
Freund, J. B., Lele, S. K. & Moin, P. 2000 Compressibility effects in a turbulent annular mixing layer. Part 1. Turbulence and growth rate. J. Fluid Mech. 421, 229–267.CrossRefGoogle Scholar
From, C. S., Sauret, E., Armfield, S. W., Saha, S. C. & Gu, Y. T. 2017 Turbulent dense gas flow characteristics in swirling conical diffuser. Comput. Fluids 149, 100–118.CrossRefGoogle Scholar
Fu, S. & Li, Q. 2006 Numerical simulation of compressible mixing layers. Intl J. Heat Fluid Flow 27 (5), 895–901.CrossRefGoogle Scholar
Garnier, E., Adams, N. & Sagaut, P. 2009 Large Eddy Simulation for Compressible Flows. Springer Science & Business Media.CrossRefGoogle Scholar
Giauque, A., Corre, C. & Menghetti, M. 2017 Direct numerical simulations of homogeneous isotropic turbulence in a dense gas. J. Phys.: Conf. Ser. 821 (1), 012017.Google Scholar
Grieser, D. R. & Goldthwaite, W. H.1963 Experimental determination of the viscosity of air in the gaseous state at low temperatures and pressures. Tech. Rep. Battelle Memorial Institute, Columbus, OH.CrossRefGoogle Scholar
Guardone, A., Vigevano, L. & Argrow, B. M. 2004 Assessment of thermodynamic models for dense gas dynamics. Phys. Fluids 16 (11), 3878–3887.CrossRefGoogle Scholar
Harinck, J., Colonna, P., Guardone, A. & Rebay, S. 2010a Influence of thermodynamic models in two-dimensional flow simulations of turboexpanders. J. Turbomach. 132 (1), 011001.CrossRefGoogle Scholar
Harinck, J., Turunen-Saaresti, T., Colonna, P., Rebay, S. & van Buijtenen, J. 2010b Computational study of a high-expansion ratio radial organic Rankine cycle turbine stator. Trans. ASME J. Engng Gas Turbines Power 132 (5), 054501.CrossRefGoogle Scholar
Hayes, W. D. 1958 The basic theory of gasdynamic discontinuities, fundamentals of gas dynamics. In High Speed Aerodynamics and Jet Propulsion (ed. Emmons, H. W.), pp. 416–481. Princeton University Press.Google Scholar
Invernizzi, C. M. 2010 Stirling engines using working fluids with strong real gas effects. Appl. Therm. Engng 30 (13), 1703–1710.CrossRefGoogle Scholar
Kirillov, N. G. 2004 Analysis of modern natural gas liquefaction technologies. Chem. Petrol. Engng 40 (7–8), 401–406.CrossRefGoogle Scholar
Kluwick, A. 2004 Internal flows of dense gases. Acta Mech. 169 (1–4), 123–143.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30 (4), 299–303.Google Scholar
Kritsuk, A. G., Norman, M. L., Paolo Padoan, A. N. D. & Wagner, R. 2007 The statistics of supersonic isothermal turbulence. Astrophys. J. 665 (1), 416–431.CrossRefGoogle Scholar
Kutateladze, S. S., Nakoryakov, V. E. & Borisov, A. A. 1987 Rarefaction waves in liquid and gas–liquid media. Annu. Rev. Fluid Mech. 19 (1), 577–600.CrossRefGoogle Scholar
Liepmann, H. W. & Laufer, J.1947 Investigations of free turbulent mixing. NACA Tech. Note 1257.Google Scholar
Luo, K. H. & Sandham, N. D. 1994 On the formation of small scales in a compressible mixing layer. In Direct and Large-Eddy Simulation I, pp. 335–346. Springer.CrossRefGoogle Scholar
Martin, J. J. & Hou, Y. 1955 Development of an equation of state for gases. AIChE J. 2 (4), 142–151.CrossRefGoogle Scholar
Martin, J. J., Kapoor, R. M. & De Nevers, N. 1959 An improved equation of state for gases. AIChE J. 5 (2), 159–160.CrossRefGoogle Scholar
Martínez Ferrer, P. J., Lehnasch, G. & Mura, A. 2017 Compressibility and heat release effects in high-speed reactive mixing layers I. Growth rates and turbulence characteristics. Combust. Flame 180 (M), 284–303.CrossRefGoogle Scholar
Mathijssen, T., Gallo, M., Casati, E., Nannan, N. R., Zamfirescu, C., Guardone, A. & Colonna, P. 2015 The flexible asymmetric shock tube (FAST): a Ludwieg tube facility for wave propagation measurements in high-temperature vapours of organic fluids. Exp. Fluids 56 (10), 1–12.Google Scholar
Menikoff, R. & Plohr, B. J. 1989 The Riemann problem for fluid flow of real materials. Rev. Mod. Phys. 61 (1), 75.CrossRefGoogle Scholar
Merle, X. & Cinnella, P. 2014 Bayesian quantification of thermodynamic uncertainties in dense gas flows. Reliability Engng Syst. Safety 134, 305–323.CrossRefGoogle Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30 (1), 539–578.CrossRefGoogle Scholar
Monaco, J. F., Cramer, M. S. & Watson, L. T. 1997 Supersonic flows of dense gases in cascade configurations. J. Fluid Mech. 330, 31–59.CrossRefGoogle Scholar
Okong’o, N. A. & Bellan, J. 2002 Direct numerical simulation of a transitional supercritical binary mixing layer: heptane and nitrogen. J. Fluid Mech. 464, 1–34.CrossRefGoogle Scholar
Pantano, C. & Sarkar, S. 2002 A study of compressibility effects in the high-speed turbulent shear layer using direct simulation. J. Fluid Mech. 451, 329–371.CrossRefGoogle Scholar
Papamoschou, D. & Roshko, A. 1988 The compressible turbulent shear layer: an experimental study. J. Fluid Mech. 197, 453–477.CrossRefGoogle Scholar
Pirozzoli, S., Bernardini, M., Marié, S. & Grasso, F. 2015 Early evolution of the compressible mixing layer issued from two turbulent streams. J. Fluid Mech. 777, 196–218.CrossRefGoogle Scholar
Poinsot, T. J. & Lele, S. K. 1992 Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101 (1), 104–129.CrossRefGoogle Scholar
Rogers, M. M. & Moser, R. D. 1994 Direct simulation of a self-similar turbulent mixing layer. Phys. Fluids 6 (2), 903–923.CrossRefGoogle Scholar
Rusak, Z. & Wang, C.-W. 1997 Transonic flow of dense gases around an airfoil with a parabolic nose. J. Fluid Mech. 346, 1–21.CrossRefGoogle Scholar
Sandham, N. D. & Reynolds, W. C. 1990 Compressible mixing layer – linear theory and direct simulation. AIAA J. 28 (4), 618–624.CrossRefGoogle Scholar
Sarkar, S. 1995 The stabilizing effect of compressibility in turbulent shear flow. J. Fluid Mech. 282, 163–186.CrossRefGoogle Scholar
Sarkar, S., Erlebacher, G., Hussaini, M. Y. & Kreiss, H. O. 1991 The analysis and modelling of dilatational terms in compressible turbulence. J. Fluid Mech. 227, 473–493.CrossRefGoogle Scholar
Sarkar, S. & Lakshmanan, B. 1991 Application of a Reynolds stress turbulence model to the compressible shear layer. AIAA J. 29 (5), 743–749.CrossRefGoogle Scholar
Sciacovelli, L., Cinnella, P., Content, C. & Grasso, F. 2016 Dense gas effects in inviscid homogeneous isotropic turbulence. J. Fluid Mech. 800, 140–179.CrossRefGoogle Scholar
Sciacovelli, L., Cinnella, P. & Gloerfelt, X. 2017a Direct numerical simulations of supersonic turbulent channel flows of dense gases. J. Fluid Mech. 821, 153–199.CrossRefGoogle Scholar
Sciacovelli, L., Cinnella, P. & Grasso, F. 2017b Small-scale dynamics of dense gas compressible homogeneous isotropic turbulence. J. Fluid Mech. 825, 515–549.CrossRefGoogle Scholar
Shuely, W. J.1996 Model liquid selection based on extreme values of liquid state properties in a factor analysis. Tech. Rep. Edgewood Research Development and Engineering Center, Aderbeen Proving Ground, MD.Google Scholar
Spinelli, A., Dossena, V., Gaetani, P., Osnaghi, C. & Colombo, D. 2010 Design of a test rig for organic vapours. In ASME Turbo Expo 2010: Power for Land, Sea, and Air, pp. 109–120. Paper N.Google Scholar
Spinelli, A., Pini, M., Dossena, V., Gaetani, P. & Casella, F. 2013 Design, simulation, and construction of a test rig for organic vapors. Trans. ASME J. Engng Gas Turbines Power 135 (4), 042304.CrossRefGoogle Scholar
Stephan, K. & Laesecke, A. 1985 The thermal conductivity of fluid air. J. Phys. Chem. Ref. Data 14 (1), 227–234.CrossRefGoogle Scholar
Stull, D. R. & Prophet, H.1971 Janaf thermochemical tables. Tech. Rep. National Standard Reference Data System.CrossRefGoogle Scholar
Sutherland, W. 1893 LII. The viscosity of gases and molecular force. Lond. Edin. Dublin Phil. Mag. J. Sci. 36 (223), 507–531.CrossRefGoogle Scholar
Tanahashi, M., Iwase, S. & Miyauchi, T. 2001 Appearance and alignment with strain rate of coherent fine scale eddies in turbulent mixing layer. J. Turbul. 2 (6), 1–17.Google Scholar
Thompson, P. A. 1971 A fundamental derivative in gasdynamics. Phys. Fluids 14 (9), 1843–1849.CrossRefGoogle Scholar
Thompson, P. A. & Lambrakis, K. C. 1973 Negative shock waves. J. Fluid Mech. 60 (1), 187–208.CrossRefGoogle Scholar
Vadrot, A., Giauque, A. & Corre, C. 2019 Investigation of turbulent dense gas flows with direct numerical simulation. In Congrès français de mécanique. AFM.Google Scholar
Vreman, A. W., Sandham, N. D. & Luo, K. H. 1996 Compressible mixing layer growth rate and turbulence characteristics. J. Fluid Mech. 320, 235–258.CrossRefGoogle Scholar
Wagner, B. & Schmidt, W. 1978 Theoretical investigations of real gas effects in cryogenic wind tunnels. AIAA J. 16 (6), 580–586.CrossRefGoogle Scholar
Wang, C.-W. & Rusak, Z. 1999 Numerical studies of transonic BZT gas flows around thin airfoils. J. Fluid Mech. 396, 109–141.CrossRefGoogle Scholar
Wang, J., Wan, M., Chen, S. & Chen, S. 2018 Kinetic energy transfer in compressible isotropic turbulence. J. Fluid Mech. 841, 581–613.CrossRefGoogle Scholar
Wheeler, A. P. S. & Ong, J. 2013 The role of dense gas dynamics on organic Rankine cycle turbine performance. Trans. ASME J. Engng Gas Turbines Power 135 (10), 102603.CrossRefGoogle Scholar
White, F. M. 1998 Fluid Mechanics. McGraw-Hill Series in Mechanical Engineering.Google Scholar
Zel’dovich, J. 1946 On the possibility of rarefaction shock waves. Zh. Eksp. Teor. Fiz. 16 (4), 363–364.Google Scholar
Zeman, O. 1990 Dilatation dissipation: the concept and application in modeling compressible mixing layers. Phys. Fluids A 2 (2), 178–188.CrossRefGoogle Scholar
Zhou, Q., He, F. & Shen, M. Y. 2012 Direct numerical simulation of a spatially developing compressible plane mixing layer: flow structures and mean flow properties. J. Fluid Mech. 711, 1–32.CrossRefGoogle Scholar