Article contents
Analysis of two interactive burning droplets with different temperatures
Published online by Cambridge University Press: 10 May 2024
Abstract
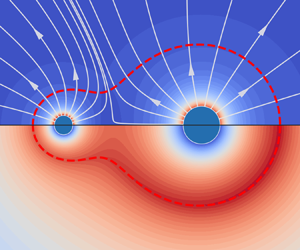
This paper presents a comprehensive theoretical analysis of the interaction between two quasi-steady burning droplets with differing temperatures, sizes and distances, building upon the mass-flux-potential model and flame-sheet assumption. In contrast to existing research, this study introduces a fresh perspective on droplet interactions by considering the different temperatures of the droplets. Utilizing the bispherical coordinate approach, theoretical solutions for the Stefan flow, scalar fields, droplet evaporation/burning rates, interaction coefficients and flame positions have been derived successfully. A comparison with extensive numerical simulations indicates a good agreement between the analytical and numerical results under a variety of conditions. It is revealed that proximity between the droplets causes non-uniform evaporation rates on their surfaces, and in some cases, leads to condensation on the cooler droplet. Notably, when the temperatures of the two droplets differ, this results in an uneven temperature distribution across the flame surface, and increasing the temperature of one droplet substantially elevates the temperature of the nearby flame. This study also establishes a criterion for the transition between different combustion modes, specifically between group and separated combustion. The findings of this study are crucial in deepening our understanding of evaporation and combustion processes, as well as the dynamics of flame spreading, local ignition, and extinction in systems involving multiple droplets.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 3
- Cited by


