Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T11:29:40.050Z Has data issue: false hasContentIssue false
  • English
  • Français

Anchoring and migration of balloon in REBOA

Published online by Cambridge University Press:  24 September 2021

C.C. Mei Open the ORCID record for C.C. Mei [Opens in a new window] ,
Y.L. Li ,
S. Michele Open the ORCID record for S. Michele [Opens in a new window] ,
P. Sammarco  and
P.B. McBeth
C.C. Mei*
Affiliation:
Dept. of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Y.L. Li
Affiliation:
Katy, TX, USA
S. Michele
Affiliation:
School of Engineering, Computing and Mathematics, University of Plymouth, Drake Circus, PlymouthPL4 8AA, UK
P. Sammarco
Affiliation:
Dept. of Civil Engineering and Computer Science, Università degli Studi di Roma ’Tor Vergata’, 00133Roma, Italy
P.B. McBeth
Affiliation:
Trauma and Acute Care Surgery, Cumming School of Medicine, University of Calgary, Calgary, AB T3M 1M4Canada
*
†Email address for correspondence: ccmei@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

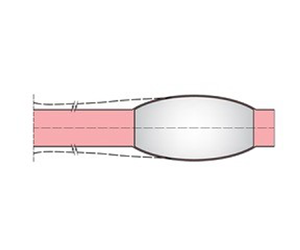
A mechanical theory is described for a phenomenon in the surgical procedure of resuscitative endovascular balloon occlusion of the aorta (REBOA). In this procedure a balloon is pushed into the aorta by a catheter and then inflated in order to stop haemorrhage. One of the hazards of this procedure is the tendency for the balloon to migrate away from its intended position. This work examines the mechanics of balloon anchoring and migration by analysing the effects of pressure waves, the sheet flow and solid friction in the thin gap between the walls of the aorta and balloon. A viscoelastic model is adopted for the aorta wall for pressure waves between the left ventricle and the balloon. The lubrication approximation is used for blood flow in the thin gap between the walls of the balloon and aorta. Samples of quantitative predictions are discussed on how the inflation pressure and balloon characteristics affect the balloon anchoring and migration. The crucial roles of solid friction and balloon placement are pointed out, which should help in guiding the manufacturing of balloons and their usage in the field.

JFM classification

Biological Fluid Dynamics: Blood flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 927 , 25 November 2021 , A20
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Armentano, R.L., Barra, J.G., Levenson, J., Simon, A. & Pinchel, R.H. 1995 a Arterial wall mechanics in conscious dogs: assessment of viscous, inertial, and elastic moduli to characterize aortic wall behavior. Circulat. Res. 76 (3), 468–478.CrossRefGoogle ScholarPubMed
Armentano, R.L., Magnien, J.L., Simon, A., Bellenfant, F., Barra, J. & Levenson, J. 1995 b Effects of hypertension on viscoelasticity of carotid and femoral arteries in humans. Hypertension 26 (1), 48–54.CrossRefGoogle ScholarPubMed
Ball, T.V. & Neufield, J.A. 2018 Static and dynamic fluid-driven fracturing of adhered elastica. Phys. Rev. Fluids 3, 074101.Google Scholar
Canic, S., Tambaca, J., Guidoboni, G., Mikelic, A., Hartlet, C.J. & Rosenstrauch, D. 2006 Modeling viscoelastic behavior of arterial walls and their interaction with pulsating blood flow. SIAM J. Appl. Maths 67 (1), 164–193.CrossRefGoogle Scholar
Caro, C.G., Pedley, T.J., Schroter, R.C. & Seed, W.A. 2011 The Mechanics of the Circulation. Cambridge University Press.CrossRefGoogle Scholar
Borger van den Burg, B.L.S., Van Schaik, J., Brouwers, J.J.W.M., Wong, C.Y.., Rasmussen, T.E., Hamming, J.F. & Hocencamp, R. 2019 Migration of aortic occlusion balloons in an in vitro model of the human circulation. Injury 50 (2), 286–291.CrossRefGoogle Scholar
Dunn, A.C., Zaveri, T.D., Keselowsky, B.G. & Sawyer, W.G. 2007 Macroscopic friction coefficient measurements on living endothelial cells. Tribol. Lett. 27 (2), 233–238.CrossRefGoogle Scholar
Elbaz, S.B. & Gat, A.D. 2016 Axial creeping flow in the gap between a rigid cylinder and a concentric elastic tube. J. Fluid Mech. 806, 580–602.CrossRefGoogle Scholar
Fitz-Gerald, J.M. 1969 Mechanics of red-cell motion through a very narrow capillaries. Proc. R. Soc. Lond. B 174, 193–227.Google ScholarPubMed
Fung, Y.C. 1997 Biomechanics, Circulation, pp. 110–142. Springer.CrossRefGoogle Scholar
Fung, Y.C. & Yih, C.S. 1968 Peristaltic transport. J. Appl. Mech. 35 (4), 669–675.CrossRefGoogle Scholar
Greenberg, H.J. 1960 Fourier analysis of the motion of a hydraulically controlled piston. IBM J. Res. Dev. 4 (4), 378–390.CrossRefGoogle Scholar
Hallock, P. & Benson, I. 1937 Studies on the elastic properties of human isolated aorta. J. Clin. Invest. 16 (4), 595–602.Google ScholarPubMed
Hewitt, I.J., Balmforth, N.J. & De Bruyn, J.R. 2015 Elastic-plated gravity currents. Eur. J. Appl. Maths 26, 1–31.CrossRefGoogle Scholar
Hughes, C.W. 1954 Use of an intra-aortic balloon catheter tamponade for controlling intra-abdominal haemorrhage in man. Surgery 36, 65–68.Google ScholarPubMed
Huppert, H.E. 1982 a Flow and instability of a viscous current down a slope. Nature 300, 427–429.CrossRefGoogle Scholar
Huppert, H.E. 1982 b The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.CrossRefGoogle Scholar
Landau, L.D. & Lifshitz, E.V. 1959 Fluid Mechanics. Pergamon.Google Scholar
Liffman, K., Sutalo, I.D., Lawrence-Brown, M.M.D., Semmens, J.B. & Aldham, B. 2006 Movement and dislocation of modular stent-grafts due to pulsatile flow and the pressure difference between the stent-graft and the aneurysm sac. J. Endovas. Therapy 13 (1), 51–61.CrossRefGoogle ScholarPubMed
Lighthill, M.J. 1968 Pressure-forcing of tightly fitting pellets along fluid-filled elastic tubes. J. Fluid Mech. 34 (part 1), 113–143.CrossRefGoogle Scholar
Lister, J.R. 1990 Buoyancy driven fluid fracture: the effects of material toughness and low viscosity precursors. J. Fluid Mech. 210, 263–280.CrossRefGoogle Scholar
Lister, J.R. 1992 Viscous flows down an inclined plane from point and line sources. J. Fluid Mech. 242, 631–653.CrossRefGoogle Scholar
Lister, J.R., Peng, G.G. & Neufeld, J.A. 2014 Viscosity controlled peeling of an elastic sheet by bending and pulling. Phys. Fluid Dyn. 14, 1–5.Google Scholar
Lukoudis, P.S. & Roos, R. 1970 The fluid mechanics of the ureter from a lubrication theory point of view. J. Fluid Mech. 43, 661–674.CrossRefGoogle Scholar
Miranker, W. 1961 A free boundary problem for the wave equation. J. Franklin Inst. 271 (4), 263–274.CrossRefGoogle Scholar
Pedley, J. 1980 The fluid mechanics of large blood vessels. Cambridge University Press.CrossRefGoogle Scholar
Petrini, L., Miglivacca, F., Massarotti, P., Schievano, S., Dubini, G. & Auricchio, F. 2005 Computational studies of shape memory alloy behavior in biomedical applications. Trans. ASME J. Biomech. Engng 127, 716–725.CrossRefGoogle ScholarPubMed
Scheisser, W. 1991 The Numerical Method of Lines: Integration of Partial Differential Equations. Academic Press.Google Scholar
Secco, G.G., et al. 2016 Very high pressure dilatation for undilatable coronary lesions: indications and results with a new dedicated balloon. Euro Intervent. 12 (3), 359–365.Google ScholarPubMed
Shapiro, A.H., Jaffrin, M.Y. & Weinberg, S.L. 1969 Peristaltic pumping with long wavelengths at low Reynolds number. J. Fluid Mech. 37 (4), 799–825.CrossRefGoogle Scholar
Sonesson, B., Hansen, F., Stale, H. & Länne, T. 1993 Compliance and diameter in the human abdominal aorta-the influence of age and sex. Eur. J. Vascu. Surg. 7, 690–697.CrossRefGoogle ScholarPubMed
Stannard, A., Eliason, J.L. & Rasmussen, T.E. 2011 Resuscitative endovascular balloon occlusion of the aorta (REBOA) as an adjunct for hemorrhagic shock. J. Trauma Injury Infect. Crit. Care 71 (6), 1869–1872.CrossRefGoogle ScholarPubMed
Trefethen, L.N. 2000 Spectral Methods in Matlab. SIAM.CrossRefGoogle Scholar
Vad, S., Eskinazi, A., Corbett, T., McLaughlin, T. & Vande Geest, J.P. 2010 Determination of coefficient of friction for self-expanding stent-grafts. J. Biomech. Engng 132, 121007.CrossRefGoogle ScholarPubMed
Wu, W., Qi, M., Liu, X., Yang, D. & Wang, W 2007 Delivery and release of nitinol stent in carotid artery and their interactions: a finite element analysis. J. Biomech. 40, 3034–3040.CrossRefGoogle ScholarPubMed