Article contents
Application of the compressible 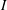 $I$-dependent rheology to chute and shear flow instabilities
$I$-dependent rheology to chute and shear flow instabilities
Published online by Cambridge University Press: 14 February 2019
Abstract
We consider the instability properties of dense granular flow in inclined plane and plane shear geometries as tests for the compressible inertial-dependent rheology. The model, which is a recent generalisation of the incompressible 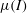 $\unicode[STIX]{x1D707}(I)$ rheology, constitutes a hydrodynamical description of dense granular flow which allows for variability in the solids volume fraction. We perform a full linear stability analysis of the model and compare its predictions to existing experimental data for glass beads on an inclined plane and discrete element simulations of plane shear in the absence of gravity. In the case of the former, we demonstrate that the compressible model can quantitatively predict the instability properties observed experimentally, and, in particular, we find that it performs better than its incompressible counterpart. For the latter, the qualitative behaviour of the plane shear instability is also well captured by the compressible model.
$\unicode[STIX]{x1D707}(I)$ rheology, constitutes a hydrodynamical description of dense granular flow which allows for variability in the solids volume fraction. We perform a full linear stability analysis of the model and compare its predictions to existing experimental data for glass beads on an inclined plane and discrete element simulations of plane shear in the absence of gravity. In the case of the former, we demonstrate that the compressible model can quantitatively predict the instability properties observed experimentally, and, in particular, we find that it performs better than its incompressible counterpart. For the latter, the qualitative behaviour of the plane shear instability is also well captured by the compressible model.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 5
- Cited by


