Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-15T06:58:39.416Z Has data issue: false hasContentIssue false
  • English
  • Français

Approach to transverse uniformity of concentration distribution of a solute in a solvent flowing along a straight pipe

Published online by Cambridge University Press:  06 February 2014

Zi Wu Open the ORCID record for Zi Wu [Opens in a new window]  and
G. Q. Chen
Zi Wu
Affiliation:
Department of Mechanics, Peking University, Beijing 100871, China
G. Q. Chen*
Affiliation:
Department of Mechanics, Peking University, Beijing 100871, China NAAM Group, King Abdulaziz University, Jeddah, Saudi Arabia
*
†Email address for correspondence: gqchen@pku.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Associated with Taylor’s classical analysis of scalar solute dispersion in the laminar flow of a solvent in a straight pipe, this work explores the approach towards transverse uniformity of concentration distribution. Mei’s homogenization technique is extended to find solutions for the concentration transport. Chatwin’s result for the approach to longitudinal normality is recovered in terms of the mean concentration over the cross-section. The asymmetrical structure of the concentration cloud and the transverse variation of the concentration distribution are concretely illustrated for the initial stage. The rate of approach to uniformity is shown to be much slower than that to normality. When the longitudinal normality of mean concentration is well established, the maximum transverse concentration difference remains near one-half of the centroid concentration of the cloud. 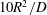A time scale up to $10 R^2/D$ (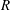$R$ is the radius of the pipe and 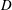$D$ is the molecular diffusivity) is suggested to characterize the transition to transverse uniformity, in contrast to the time scale of 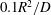$0.1 R^2/D$ estimated by Taylor for the initial stage of dispersion, and that of 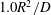$1.0 R^2/D$ by Chatwin for longitudinal normality.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 740 , 10 February 2014 , pp. 196 - 213
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajdari, A., Bontoux, N. & Stone, H. A. 2006 Hydrodynamic dispersion in shallow microchannels: the effect of cross-sectional shape. Analyt. Chem. 78, 387–392.Google Scholar
Aris, R. 1956 On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. A 235, 67–77.Google Scholar
Aris, R. 1959 On the dispersion of a solute by diffusion, convection and exchange between phases. Proc. R. Soc. Lond. A 252, 538–550.Google Scholar
Chatwin, P. C. 1970 Approach to normality of concentration distribution of a solute in a solvent flowing along a straight pipe. J. Fluid Mech. 43, 321–352.CrossRefGoogle Scholar
Chen, G. Q. & Wu, Z. 2012 Taylor dispersion in a two-zone packed tube. Intl J. Heat Mass Transfer 55, 43–52.Google Scholar
Chen, G. Q., Wu, Z. & Zeng, L. 2012 Environmental dispersion in a two-layer wetland: analytical solution by method of concentration moments. Intl J. Engng Sci. 51, 272–291.Google Scholar
Chen, Z. & Chauhan, A. 2005 DNA separation by EFFF in a microchannel. J. Colloid Interface Sci. 285, 834–844.CrossRefGoogle Scholar
Fischer, H. B. 1976 Mixing and dispersion in estuaries. Annu. Rev. Fluid Mech. 8, 107–133.Google Scholar
Fischer, H. B., List, E. J., Koh, R. C. Y., Imberger, J. & Brooks, N. H. 1979 Mixing in Inland and Coastal Waters. Academic Press.Google Scholar
Gill, W. N. 1967 A note on solution of transient dispersion problems. Proc. R. Soc. Lond. A 298, 335–339.Google Scholar
Gill, W. N. & Sankaras, R. 1970 Exact analysis of unsteady convective diffusion. Proc. R. Soc. Lond. A 316, 341–350.Google Scholar
Gill, W. N. & Sankarasubramanian, R. 1971 Dispersion of a non-uniform slug in time-dependent flow. Proc. R. Soc. Lond. A 322, 101–117.Google Scholar
Holley, E. R., Harleman, D. R. F. & Fischer, H. B. 1970 Dispersion in homogeneous estuary flow. J. Hydraul. Engng 96, 1691–1709.Google Scholar
Houseworth, J. E. 1984 Shear dispersion and residence time for laminar-flow in capillary tubes. J. Fluid Mech. 142, 289–308.CrossRefGoogle Scholar
Latini, M. & Bernoff, A. J. 2001 Transient anomalous diffusion in Poiseuille flow. J. Fluid Mech. 441, 399–411.Google Scholar
Lighthill, M. J. 1966 Initial development of diffusion in Poiseuille flow. IMA J. Appl. Maths 2, 97–108.Google Scholar
Mei, C. C.Dispersion of suspension in a steady shear flow. Lecture Notes in Fluid Dynamics, 1.63J/2.01J. MIT.Google Scholar
Mei, C. C., Auriault, J. L. & Ng, C. O. 1996 Some applications of the homogenization theory. Adv. Appl. Mech. 32, 277–348.CrossRefGoogle Scholar
Ng, C. O. 2000 Chemical transport associated with discharge of contaminated fine particles to a steady open-channel flow. Phys. Fluids 12, 136–144.CrossRefGoogle Scholar
Ng, C. O. 2006 Dispersion in steady and oscillatory flows through a tube with reversible and irreversible wall reactions. Proc. R. Soc. Lond. A 462, 481–515.Google Scholar
Ng, C. O. & Yip, T. L. 2001 Effects of kinetic sorptive exchange on solute transport in open-channel flow. J. Fluid Mech. 446, 321–345.Google Scholar
Paul, S. & Mazumder, B. S. 2011 Effects of nonlinear chemical reactions on the transport coefficients associated with steady and oscillatory flows through a tube. Intl J. Heat Mass Transfer 54, 75–85.Google Scholar
Phillips, C. G. & Kaye, S. R. 1996 A uniformly asymptotic approximation for the development of shear dispersion. J. Fluid Mech. 329, 413–443.CrossRefGoogle Scholar
Phillips, C. G. & Kaye, S. R. 1997 The initial transient of concentration during the development of Taylor dispersion. Proc. R. Soc. Lond. A 453, 2669–2688.CrossRefGoogle Scholar
Ratnakar, R. R. & Balakotaiah, V. 2011 Exact averaging of laminar dispersion. Phys. Fluids 23, 023601.CrossRefGoogle Scholar
Ratnakar, R. R., Bhattacharya, M. & Balakotaiah, V. 2012 Reduced order models for describing dispersion and reaction in monoliths. Chem. Engng Sci. 83, 77–92.CrossRefGoogle Scholar
Shankar, A. & Lenhoff, A. M. 1991 Dispersion in round tubes and its implications for extra-column dispersion. J. Chromatogr. 556, 235–248.CrossRefGoogle Scholar
Smith, R. 1982 Contaminant dispersion in oscillatory flows. J. Fluid Mech. 114, 379–398.Google Scholar
Smith, R. 1983 The contraction of contaminant distributions in reversing flows. J. Fluid Mech. 129, 137–151.Google Scholar
Stokes, A. N. & Barton, N. G. 1990 The concentration distribution produced by shear dispersion of solute in Poiseuille flow. J. Fluid Mech. 210, 201–221.CrossRefGoogle Scholar
Stone, H. A. & Brenner, H. 1999 Dispersion in flows with streamwise variations of mean velocity: radial flow. Ind. Engng Chem. Res. 38, 851–854.Google Scholar
Taylor, G. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Vrentas, J. S. & Vrentas, C. M. 2000 Asymptotic solutions for laminar dispersion in circular tubes. Chem. Engng Sci. 55, 849–855.Google Scholar
Wu, Z. & Chen, G. Q. 2012 Dispersion in a two-zone packed tube: an extended Taylor’s analysis. Intl J. Engng Sci. 50, 113–123.CrossRefGoogle Scholar
Wu, Z., Li, Z. & Chen, G. Q. 2011 Multi-scale analysis for environmental dispersion in wetland flow. Commun. Nonlinear Sci. Numer. Simul. 16, 3168–3178.CrossRefGoogle Scholar
Wu, Z., Zeng, L., Chen, G. Q., Li, Z., Shao, L., Wang, P. & Jiang, Z. 2012 Environmental dispersion in a tidal flow through a depth-dominated wetland. Commun. Nonlinear Sci. Numer. Simul. 17, 5007–5025.CrossRefGoogle Scholar
Yasuda, H. 1984 Longitudinal dispersion of matter due to the shear effect of steady and oscillatory currents. J. Fluid Mech. 148, 383–403.Google Scholar
Zeng, L.2010 Analytical study on environmental dispersion in wetland flow. PhD dissertation, Peking University, Beijing.Google Scholar
Zeng, L., Chen, G. Q., Wu, Z., Li, Z., Wu, Y. H. & Ji, P. 2012 Flow distribution and environmental dispersivity in a tidal wetland channel of rectangular cross-section. Commun. Nonlinear Sci. Numer. Simul. 17, 4192–4209.CrossRefGoogle Scholar