Article contents
Asymptotic theory of Mack-mode receptivity in hypersonic boundary layers due to interaction of a heating/cooling source and a freestream sound wave
Published online by Cambridge University Press: 22 May 2023
Abstract
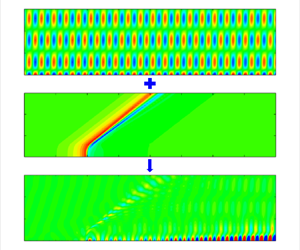
In this paper, we study the local receptivity of the inviscid Mack modes in hypersonic boundary layers induced by the interaction between a surface heating or cooling source (HCS) and a freestream acoustic wave. The asymptotic analysis reveals that among the three distinguished layers, i.e. the main, wall and Stokes layers, the leading-order receptivity is attributed to the interaction of the HCS-induced mean-flow distortion and the acoustic signature in the wall layer; the second-order contribution appears in the Stokes layer; the third-order contribution appears in both the main and wall layers. Interestingly, at a moderate Reynolds number, the third-order contribution to the receptivity efficiency may be quantitatively greater than the second-order one, but this does not lead to breakdown of this asymptotic theory. Assuming the HCS intensity to be sufficiently weak, the asymptotic predictions are made for four representative cases involving different Mach numbers and wall temperatures, which are compared with the results obtained by the finite-Reynolds-number theory based on either the extended compressible Orr–Sommerfeld equations or the harmonic linearised Navier–Stokes (HLNS) calculations. Taking into account the first three orders of the receptivity efficiency, the asymptotic predictions are confirmed to be sufficiently accurate even when the Reynolds number is a few thousands, and the agreement with the finite-Reynolds-number calculations is better when the wall temperature of the base flow approaches the adiabatic wall temperature. The HLNS calculations are also conducted for moderate HCS intensities. It is found that the nonlinearity does not affect the receptivity coefficient much even when the temperature distortion of the HCS reaches  $80\,\%$ of the temperature at the wall.
$80\,\%$ of the temperature at the wall.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 9
- Cited by


