Article contents
Axial flow in a two-dimensional microchannel induced by a travelling temperature wave imposed at the bottom wall
Published online by Cambridge University Press: 13 June 2018
Abstract
Fluid flow in microchannels has wide industrial and scientific applications. Hence, it is important to explore different driving mechanisms. In this paper, we study the net transport or fluid pumping in a two-dimensional channel induced by a travelling temperature wave applied at the bottom wall. The Navier–Stokes equations with the Boussinesq approximation and the convection–diffusion heat equation are made dimensionless by the height of the channel and a velocity scale obtained by a dominant balance between buoyancy and viscous resistance in the momentum equation. The system of equations is transformed to an axial coordinate that moves with the travelling temperature wave, and we seek steady solutions in this moving frame. Four dimensionless numbers emerge from the governing equations and boundary conditions: the Reynolds number 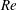 $Re$ , a Reynolds number
$Re$ , a Reynolds number 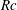 $Rc$ based on the wave speed, the Prandtl number
$Rc$ based on the wave speed, the Prandtl number 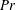 $Pr$ and the dimensionless wavenumber
$Pr$ and the dimensionless wavenumber 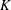 $K$ . The system of equations is solved by a finite-volume method and by a perturbation method in the limit
$K$ . The system of equations is solved by a finite-volume method and by a perturbation method in the limit 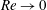 $Re\rightarrow 0$ . Surprisingly, the leading and first-order perturbation solutions agree well with the computed axial flow for
$Re\rightarrow 0$ . Surprisingly, the leading and first-order perturbation solutions agree well with the computed axial flow for 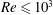 $Re\leqslant 10^{3}$ . Thus, the analytic perturbation solutions are used to study systematically the effects of
$Re\leqslant 10^{3}$ . Thus, the analytic perturbation solutions are used to study systematically the effects of 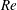 $Re$ ,
$Re$ , 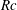 $Rc$ ,
$Rc$ , 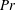 $Pr$ and
$Pr$ and 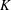 $K$ on the dimensionless induced axial flow
$K$ on the dimensionless induced axial flow 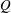 $Q$ . We find that
$Q$ . We find that 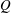 $Q$ varies linearly with
$Q$ varies linearly with  $Re$ , and
$Re$ , and 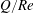 $Q/Re$ versus any of the three remaining dimensionless groups always exhibits a maximum. The global maximum of
$Q/Re$ versus any of the three remaining dimensionless groups always exhibits a maximum. The global maximum of 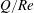 $Q/Re$ in the parameter space is subsequently determined for the first time. This induced axial flow is driven solely by the Reynolds stress.
$Q/Re$ in the parameter space is subsequently determined for the first time. This induced axial flow is driven solely by the Reynolds stress.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 1
- Cited by


