Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T17:17:55.545Z Has data issue: false hasContentIssue false
  • English
  • Français

Azimuthal diffusion of the large-scale-circulation plane, and absence of significant non-Boussinesq effects, in turbulent convection near the ultimate-state transition

Published online by Cambridge University Press:  17 February 2016

Xiaozhou He ,
Eberhard Bodenschatz  and
Guenter Ahlers
Xiaozhou He
Affiliation:
Max Planck Institute for Dynamics and Self Organization (MPIDS), D-37073 Göttingen, Germany Institute for Turbulence–Noise–Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China International Collaboration for Turbulence Research
Eberhard Bodenschatz
Affiliation:
Max Planck Institute for Dynamics and Self Organization (MPIDS), D-37073 Göttingen, Germany Institute for Nonlinear Dynamics, University of Göttingen, D-37073 Göttingen, Germany Laboratory of Atomic and Solid-State Physics and Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA International Collaboration for Turbulence Research
Guenter Ahlers*
Affiliation:
Max Planck Institute for Dynamics and Self Organization (MPIDS), D-37073 Göttingen, Germany Department of Physics, University of California, Santa Barbara, CA 93106, USA International Collaboration for Turbulence Research
*
†Email address for correspondence: guenter@physics.ucsb.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present measurements of the orientation 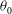${\it\theta}_{0}$ and temperature amplitude 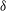${\it\delta}$ of the large-scale circulation in a cylindrical sample of turbulent Rayleigh–Bénard convection (RBC) with aspect ratio 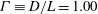${\it\Gamma}\equiv D/L=1.00$ (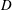$D$ and 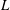$L$ are the diameter and height respectively) and for the Prandtl number 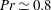$Pr\simeq 0.8$. The results for 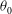${\it\theta}_{0}$ revealed a preferred orientation with up-flow in the west, consistent with a broken azimuthal invariance due to the Earth’s Coriolis force (see Brown & Ahlers (Phys. Fluids, vol. 18, 2006, 125108)). They yielded the azimuthal diffusivity 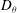$D_{{\it\theta}}$ and a corresponding Reynolds number 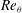$Re_{{\it\theta}}$ for Rayleigh numbers over the range 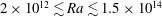$2\times 10^{12}\lesssim Ra\lesssim 1.5\times 10^{14}$. In the classical state (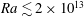$Ra\lesssim 2\times 10^{13}$) the results were consistent with the measurements by Brown & Ahlers (J. Fluid Mech., vol. 568, 2006, pp. 351–386) for 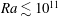$Ra\lesssim 10^{11}$ and 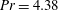$Pr=4.38$, which gave 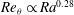$Re_{{\it\theta}}\propto Ra^{0.28}$, and with the Prandtl-number dependence 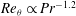$Re_{{\it\theta}}\propto Pr^{-1.2}$ as found previously also for the velocity-fluctuation Reynolds number 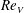$Re_{V}$ (He et al., New J. Phys., vol. 17, 2015, 063028). At larger 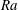$Ra$ the data for 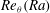$Re_{{\it\theta}}(Ra)$ revealed a transition to a new state, known as the ‘ultimate’ state, which was first seen in the Nusselt number 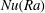$Nu(Ra)$ and in 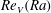$Re_{V}(Ra)$ at 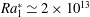$Ra_{1}^{\ast }\simeq 2\times 10^{13}$ and 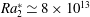$Ra_{2}^{\ast }\simeq 8\times 10^{13}$. In the ultimate state we found 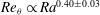$Re_{{\it\theta}}\propto Ra^{0.40\pm 0.03}$. Recently, Skrbek & Urban (J. Fluid Mech., vol. 785, 2015, pp. 270–282) claimed that non-Oberbeck–Boussinesq effects on the Nusselt and Reynolds numbers of turbulent RBC may have been interpreted erroneously as a transition to a new state. We demonstrate that their reasoning is incorrect and that the transition observed in the Göttingen experiments and discussed in the present paper is indeed to a new state of RBC referred to as ‘ultimate’.

JFM classification

Turbulent Flows: Turbulent convection
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , R3
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G. 2009 Turbulent convection. Physics 2, 74.CrossRefGoogle Scholar
Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. & Verzicco, R. 2012a Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.Google Scholar
Ahlers, G., Bodenschatz, E. & He, X. 2014 Logarithmic temperature profiles of turbulent Rayleigh–Bénard convection in the classical and ultimate state for a Prandtl number of 0.8. J. Fluid Mech. 758, 436–467.CrossRefGoogle Scholar
Ahlers, G., Brown, E., Fontenele Araujo, F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck–Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.Google Scholar
Ahlers, G., Calzavarini, E., Fontenele Araujo, F., Funfschilling, D., Grossmann, S., Lohse, D. & Sugiyama, K. 2008 Non-Oberbeck–Boussinesq effects in turbulent thermal convection in ethane close to the critical point. Phys. Rev. E 77, 046302.CrossRefGoogle Scholar
Ahlers, G., Dressel, B., Oh, J. & Pesch, W. 2009a Strong non-Boussinesq effects near the onset of convection in a fluid near its critical point. J. Fluid Mech. 642, 15–48.CrossRefGoogle Scholar
Ahlers, G., Funfschilling, D. & Bodenschatz, E. 2009b Transitions in heat transport by turbulent convection for $Pr=0.8$ and $10^{11}\leqslant Ra\leqslant 10^{15}$ . New J. Phys. 11, 123001.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009c Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–538.CrossRefGoogle Scholar
Ahlers, G., He, X., Funfschilling, D. & Bodenschatz, E. 2012b Heat transport by turbulent Rayleigh–Bénard convection for $Pr\simeq 0.8$ and $3\times 10^{12}\lesssim Ra\lesssim 10^{15}$ : aspect ratio ${\it\gamma}=0.50$ . New J. Phys. 14, 103012.Google Scholar
Boussinesq, J. 1903 Theorie Analytique de la Chaleur, vol. 2. Gauthier-Villars.Google Scholar
Brown, E. & Ahlers, G. 2006a Effect of the Earth’s Coriolis force on turbulent Rayleigh–Bénard convection in the laboratory. Phys. Fluids 18, 125108.Google Scholar
Brown, E. & Ahlers, G. 2006b Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2007a Large-scale circulation model of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 134501.Google Scholar
Brown, E. & Ahlers, G. 2007b Temperature gradients, and search for non-Boussinesq effects, in the interior of turbulent Rayleigh–Bénard convection. Europhys. Lett. 80, 14001.Google Scholar
Brown, E. & Ahlers, G. 2008 A model of diffusion in a potential well for the dynamics of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20, 075101.Google Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.Google Scholar
Burnishev, Y., Segre, E. & Steinberg, V. 2010 Strong symmetrical non-Oberbeck–Boussinesq turbulent convection and the role of compressibility. Phys. Fluids 22, 035108.CrossRefGoogle Scholar
Burnishev, Y. & Steinberg, V. 2012 Statistics and scaling properties of temperature field in symmetrical non-Oberbeck–Boussinesq turbulent convection. Phys. Fluids 24, 045102.Google Scholar
Busse, F. H. 1967 The stability of finite amplitude cellular convection and its relation to an extremum principle. J. Fluid Mech. 30, 625–649.Google Scholar
Chavanne, X., Chilla, F., Castaing, B., Hebral, B., Chabaud, B. & Chaussy, J. 1997 Observation of the ultimate regime in Rayleigh–Bénard convection. Phys. Rev. Lett. 79, 3648–3651.Google Scholar
Chavanne, X., Chilla, F., Chabaud, B., Castaing, B. & Hebral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300–1320.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.Google Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
van Gils, D. P. M., Huisman, S. G., Briggert, G.-W., Sun, C. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co- and counterrotating cylinders. Phys. Rev. Lett. 106, 024502.Google Scholar
van Gils, D., Huisman, S., Grossmann, S., Sun, C. & Lohse, D. 2012 Optimal Taylor–Couette turbulence. J. Fluid Mech. 706, 118–149.Google Scholar
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016305.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.Google Scholar
Grossmann, S. & Lohse, D. 2012 Logarithmic temperature profiles in the ultimate regime of thermal convection. Phys. Fluids 24, 125103.Google Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48, 53–80.Google Scholar
He, X., Funfschilling, D., Bodenschatz, E. & Ahlers, G. 2012a Heat transport by turbulent Rayleigh–Bénard convection for $Pr\simeq 0.8$ and $4\times 10^{11}\lesssim Ra\lesssim 2\times 10^{14}$ : ultimate-state transition for aspect ratio ${\it\gamma}=1.00$ . New J. Phys. 14, 063030.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012b Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2013 Comment on ‘Effect of boundary layers asymmetry on heat transfer efficiency in turbulent Rayleigh–Bénard convection at very high Rayleigh numbers by Urban et al.?’. Phys. Rev. Lett. 110, 199401.Google Scholar
He, X., van Gils, D., Bodenschatz, E. & Ahlers, G. 2014 Logarithmic spatial variations and universal $f^{-1}$ power spectra of temperature fluctuations in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 112, 174501.Google Scholar
He, X., van Gils, D., Bodenschatz, E. & Ahlers, G. 2015 Reynolds numbers and the elliptic approximation near the ultimate state of turbulent Rayleigh–Bénard convection. New J. Phys. 17, 063028.Google Scholar
Huisman, S. G., van Gils, D. P. M., Grossmann, S., Sun, C. & Lohse, D. 2012 Ultimate turbulent Taylor–Couette flow. Phys. Rev. Lett. 108, 024501.Google Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54 (8), 34–39.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbritrary Prandtl number. Phys. Fluids 5, 1374–1389.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics. Pergamon.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Oberbeck, A. 1879 Über die Wärmeleitung der Flüssigkeiten bei Berücksichtigung der Strömungen infolge von Temperaturdifferenzen. Ann. Phys. Chem. 7, 271–292.Google Scholar
Ostilla, R., Stevens, R., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulation. J. Fluid Mech. 719, 14–46.Google Scholar
Ostilla-Monico, R., van der Poel, E., Verzicco, R., Grossmann, S. & Lohse, D. 2014 Exploring the phase diagram of fully turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.Google Scholar
Roche, P.-E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New J. Phys. 12, 085014.CrossRefGoogle Scholar
Skrbek, L. & Urban, P. 2015 Has the ultimate state of turbulent thermal convection been observed? J. Fluid Mech. 785, 270–282.Google Scholar
Spiegel, E. A. 1971 Convection in stars. Annu. Rev. Astron. Astrophys. 9, 323–352.CrossRefGoogle Scholar
Stevens, R. J., Clercx, H. J. & Lohse, D. 2011 Effect of plumes on measuring the large scale circulation. Phys. Fluids 23, 095110.Google Scholar
Wei, P. & Ahlers, G. 2014 Logarithmic temperature distribution in the bulk of turbulent Rayleigh–Bénard convection for a Prandtl number of 12.3. J. Fluid Mech. 758, 809–830.Google Scholar
Weiss, S. & Ahlers, G. 2011 The large-scale flow structure in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 461–492.Google Scholar
Zhong, J.-Q., Funfschilling, D. & Ahlers, G. 2009 Enhanced heat transport by turbulent two-phase Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 124501.Google Scholar