No CrossRef data available.
Published online by Cambridge University Press: 01 March 2023
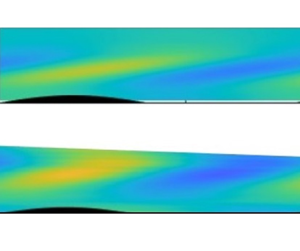
The present paper investigates theoretically and experimentally the boundary layer generated by a stably stratified fluid flowing horizontally along a surface tilted in the transverse direction and deformed by sinusoidal undulations with crests perpendicular to the flow direction. In the absence of undulations, a weak transverse velocity proportional to the normal velocity is created such that the flow remains purely horizontal. In the presence of undulations of amplitude  $h$, a stronger transverse flow is generated that exhibits a singular behaviour at the critical altitude where the frequency of the perturbation matches the buoyancy frequency of the fluid. This baroclinic critical layer was previously analysed by Passaggia et al. (J. Fluid Mech., vol. 751, 2014, pp. 663–684) for a boundary layer flow with a small sliding velocity on the surface. Here, the no-slip boundary condition of the experimental flow is applied. For this purpose, we solve the viscous sub-layer to obtain a complete theoretical model for the solution in the critical layer without any adjusting parameter. The theoretical predictions for the transverse velocity are compared with experimental measurements, and a good quantitative agreement is demonstrated. Compared with the sliding case, the no-slip boundary condition on the surface reduces the amplitude of the critical layer solution by a factor
$h$, a stronger transverse flow is generated that exhibits a singular behaviour at the critical altitude where the frequency of the perturbation matches the buoyancy frequency of the fluid. This baroclinic critical layer was previously analysed by Passaggia et al. (J. Fluid Mech., vol. 751, 2014, pp. 663–684) for a boundary layer flow with a small sliding velocity on the surface. Here, the no-slip boundary condition of the experimental flow is applied. For this purpose, we solve the viscous sub-layer to obtain a complete theoretical model for the solution in the critical layer without any adjusting parameter. The theoretical predictions for the transverse velocity are compared with experimental measurements, and a good quantitative agreement is demonstrated. Compared with the sliding case, the no-slip boundary condition on the surface reduces the amplitude of the critical layer solution by a factor  $Re^{-1/3}$, where the Reynolds number Re is defined using the velocity at infinity and the thickness of the boundary layer. As a consequence, the transverse velocity has a maximum in the critical layer of order
$Re^{-1/3}$, where the Reynolds number Re is defined using the velocity at infinity and the thickness of the boundary layer. As a consequence, the transverse velocity has a maximum in the critical layer of order  $h$, but it still induces a shear rate of order
$h$, but it still induces a shear rate of order  $h\,Re^{1/3}$.
$h\,Re^{1/3}$.