Article contents
Benjamin’s gravity current into an ambient fluid with an open surface
Published online by Cambridge University Press: 19 July 2017
Abstract
We present the solution of the idealized steady-state gravity current of height 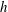 $h$ and density
$h$ and density 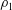 $\unicode[STIX]{x1D70C}_{1}$ that propagates into an ambient motionless fluid of height
$\unicode[STIX]{x1D70C}_{1}$ that propagates into an ambient motionless fluid of height 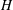 $H$ and density
$H$ and density 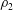 $\unicode[STIX]{x1D70C}_{2}$ with an upper surface open to the atmosphere (open channel) at high Reynolds number. The current propagates with speed
$\unicode[STIX]{x1D70C}_{2}$ with an upper surface open to the atmosphere (open channel) at high Reynolds number. The current propagates with speed 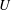 $U$ and causes a depth decrease
$U$ and causes a depth decrease 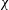 $\unicode[STIX]{x1D712}$ of the top surface. This is a significant extension of Benjamin’s (J. Fluid Mech., vol. 31, 1968, pp. 209–248) seminal solution for a fixed-top channel (
$\unicode[STIX]{x1D712}$ of the top surface. This is a significant extension of Benjamin’s (J. Fluid Mech., vol. 31, 1968, pp. 209–248) seminal solution for a fixed-top channel (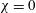 $\unicode[STIX]{x1D712}=0$). In the present case, the determination of
$\unicode[STIX]{x1D712}=0$). In the present case, the determination of 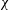 $\unicode[STIX]{x1D712}$ is part of the problem. The dimensionless parameters of the problem are
$\unicode[STIX]{x1D712}$ is part of the problem. The dimensionless parameters of the problem are 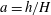 $a=h/H$ and
$a=h/H$ and 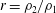 $r=\unicode[STIX]{x1D70C}_{2}/\unicode[STIX]{x1D70C}_{1}$. We show that a control-volume analysis determines
$r=\unicode[STIX]{x1D70C}_{2}/\unicode[STIX]{x1D70C}_{1}$. We show that a control-volume analysis determines 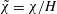 $\tilde{\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D712}/H$ and
$\tilde{\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D712}/H$ and 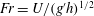 $\mathit{Fr}=U/(g^{\prime }h)^{1/2}$ as functions of
$\mathit{Fr}=U/(g^{\prime }h)^{1/2}$ as functions of  $a$ and
$a$ and  $r$, where
$r$, where 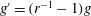 $g^{\prime }=(r^{-1}-1)g$ is the reduced gravity. The system satisfies balance of volume and momentum (explicitly), and vorticity (implicitly). We develop two branches (models) of solution for the control-volume balances. The first assumes that the outflow velocity
$g^{\prime }=(r^{-1}-1)g$ is the reduced gravity. The system satisfies balance of volume and momentum (explicitly), and vorticity (implicitly). We develop two branches (models) of solution for the control-volume balances. The first assumes that the outflow velocity 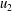 $u_{2}$ is
$u_{2}$ is  $z$-independent, accompanied by a similarly homogeneous headloss; this model is exactly the counterpart of Benjamin’s solution (
$z$-independent, accompanied by a similarly homogeneous headloss; this model is exactly the counterpart of Benjamin’s solution ( $z$ is the vertical coordinate). The second model assumes that
$z$ is the vertical coordinate). The second model assumes that 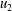 $u_{2}$ increases from
$u_{2}$ increases from 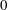 $0$ in a layer of finite thickness
$0$ in a layer of finite thickness 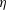 $\unicode[STIX]{x1D702}$ (say) above the
$\unicode[STIX]{x1D702}$ (say) above the 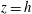 $z=h$ interface, and the headloss occurs in this layer only (a vortex wake). The
$z=h$ interface, and the headloss occurs in this layer only (a vortex wake). The 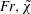 $\mathit{Fr},\tilde{\unicode[STIX]{x1D712}}$ results of these models are in excellent agreement, and this increases the confidence concerning the physical relevance of the analysis. (The solution is obtained numerically.) The predicted flows are in general dissipative, and thus physically energetically valid only for
$\mathit{Fr},\tilde{\unicode[STIX]{x1D712}}$ results of these models are in excellent agreement, and this increases the confidence concerning the physical relevance of the analysis. (The solution is obtained numerically.) The predicted flows are in general dissipative, and thus physically energetically valid only for 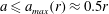 $a\leqslant a_{max}(r)\approx 0.5r$, where non-negative dissipation appears. In this range of validity, the open-surface
$a\leqslant a_{max}(r)\approx 0.5r$, where non-negative dissipation appears. In this range of validity, the open-surface 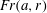 $\mathit{Fr}(a,r)$ is smaller than Benjamin’s
$\mathit{Fr}(a,r)$ is smaller than Benjamin’s 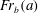 $\mathit{Fr}_{b}(a)$, but the reduction is not dramatic, typically a few per cent. The current with thickness
$\mathit{Fr}_{b}(a)$, but the reduction is not dramatic, typically a few per cent. The current with thickness 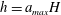 $h=a_{max}H$ is energy conserving. For given
$h=a_{max}H$ is energy conserving. For given  $r$, the energy conserving
$r$, the energy conserving 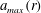 $a_{max}(r)$ provides the maximum height depression
$a_{max}(r)$ provides the maximum height depression 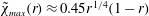 $\tilde{\unicode[STIX]{x1D712}}_{max}(r)\approx 0.45r^{1/4}(1-r)$. The largest possible depression is
$\tilde{\unicode[STIX]{x1D712}}_{max}(r)\approx 0.45r^{1/4}(1-r)$. The largest possible depression is 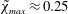 $\tilde{\unicode[STIX]{x1D712}}_{max}\approx 0.25$ at
$\tilde{\unicode[STIX]{x1D712}}_{max}\approx 0.25$ at 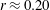 $r\approx 0.20$, and this corresponds to the minimum of
$r\approx 0.20$, and this corresponds to the minimum of 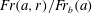 $\mathit{Fr}(a,r)/\mathit{Fr}_{b}(a)$ which is approximately 0.75. For
$\mathit{Fr}(a,r)/\mathit{Fr}_{b}(a)$ which is approximately 0.75. For 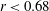 $r<0.68$, the propagation is subcritical; for
$r<0.68$, the propagation is subcritical; for 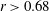 $r>0.68$, the subcritical flow condition reduces the applicability slightly to
$r>0.68$, the subcritical flow condition reduces the applicability slightly to 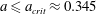 $a\leqslant a_{\mathit{crit}}\approx 0.345$. For a Boussinesq system with
$a\leqslant a_{\mathit{crit}}\approx 0.345$. For a Boussinesq system with 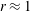 $r\approx 1$, we obtain
$r\approx 1$, we obtain 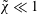 $\tilde{\unicode[STIX]{x1D712}}\ll 1$, and the present
$\tilde{\unicode[STIX]{x1D712}}\ll 1$, and the present 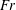 $\mathit{Fr}$, dissipation and
$\mathit{Fr}$, dissipation and 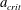 $a_{\mathit{crit}}$ results differ only slightly from Benjamin’s classical predictions, as expected.
$a_{\mathit{crit}}$ results differ only slightly from Benjamin’s classical predictions, as expected.
- Type
- Rapids
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 8
- Cited by



