Published online by Cambridge University Press: 27 February 2019
We develop a bifurcation theory describing the conditions under which vortices are created or destroyed in a two-dimensional incompressible flow. We define vortices using the 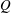 $Q$-criterion and analyse the vortex structure by considering the evolution of the zero contours of
$Q$-criterion and analyse the vortex structure by considering the evolution of the zero contours of 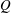 $Q$. The theory identifies topological changes of the vortex structure and classifies these as four possible types of bifurcations, two occurring away from boundaries, and two occurring near no-slip walls. Our theory provides a description of all possible codimension-one bifurcations where time is treated as the bifurcation parameter. To illustrate our results, we consider the early stages of boundary layer eruption at moderate Reynolds numbers in the range from
$Q$. The theory identifies topological changes of the vortex structure and classifies these as four possible types of bifurcations, two occurring away from boundaries, and two occurring near no-slip walls. Our theory provides a description of all possible codimension-one bifurcations where time is treated as the bifurcation parameter. To illustrate our results, we consider the early stages of boundary layer eruption at moderate Reynolds numbers in the range from 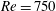 $Re=750$ to
$Re=750$ to 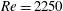 $Re=2250$. By analysing numerical simulations of the phenomenon, we show how to describe the eruption process as sequences of the four possible bifurcations of codimension one. Our simulations show that there is a single codimension-two point within our parameter range. This codimension-two point arises at
$Re=2250$. By analysing numerical simulations of the phenomenon, we show how to describe the eruption process as sequences of the four possible bifurcations of codimension one. Our simulations show that there is a single codimension-two point within our parameter range. This codimension-two point arises at 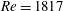 $Re=1817$ via the coalescence of two codimension-one bifurcations which are associated with the creation and subsequent destruction of one of the vortices that erupt from the boundary layer. We present a theoretical description of this process and explain how the occurrence of this phenomenon separates the parameter space into two regions with distinct evolution of the topology of the vortices.
$Re=1817$ via the coalescence of two codimension-one bifurcations which are associated with the creation and subsequent destruction of one of the vortices that erupt from the boundary layer. We present a theoretical description of this process and explain how the occurrence of this phenomenon separates the parameter space into two regions with distinct evolution of the topology of the vortices.