1. Introduction
In flow control applications, model-based and rigorous design of controllers, using both experimental and simulation data, yields important insights into physical fluid systems for effective transition control. However, a major difficulty is to design feedback controllers for high-dimensional systems, such as those obtained by experiments or high-fidelity simulations, because of the prohibitive time and resource requirements. A more effective alternative is to rely on physical insights (Sturzebecher & Nitsche Reference Sturzebecher and Nitsche2003; Opfer et al. Reference Opfer, Evert, Ronneberger and Grosche2004; Li & Gaster Reference Li and Gaster2006; Greenblatt et al. Reference Greenblatt, Goeksel, Rechenberg, Schüle, Romann and Paschereit2008; Amitay, Tuna & Dell'Orso Reference Amitay, Tuna and Dell'Orso2016; Vadarevu et al. Reference Vadarevu, Symon, Illingworth and Marusic2019) to obtain approximations and simplifications for the governing equations, or to approximate the high-dimensional system using reduced-order models (Taylor & Glauser Reference Taylor and Glauser2004; Rowley Reference Rowley2005; Schmid Reference Schmid2010; Brunton, Rowley & Williams Reference Brunton, Rowley and Williams2013; Semeraro et al. Reference Semeraro, Bagheri, Brandt and Henningson2013; Nicolò et al. Reference Fabbiane, Simon, Fischer, Grundmann, Bagheri and Henningson2015; Sipp & Schmid Reference Sipp and Schmid2016; Taira et al. Reference Taira, Brunton, Dawson, Rowley, Colonius, McKeon, Schmidt, Gordeyev, Theofilis and Ukeiley2017) that retain those aspects of the flow that are relevant from a control perspective (Kim & Bewley Reference Kim and Bewley2007).
Following the new identification and isolation paradigm recently introduced by the authors (Gluzman, Oshman & Cohen Reference Gluzman, Oshman and Cohen2020), in this paper we employ an alternative modelling approach that focuses on the physical disturbances that affect the flow field, such as those generated by sound or vorticity in the free stream, or by acoustic, mechanical or electrical actuators. These disturbances can modify the state of the field, i.e. its velocity, temperature or pressure, at a certain combination of position and time. The information we base on consists of flow field measurements that are acquired by sensors embedded in the field. We regard these measurements as consisting of mixtures of disturbance sources, where a disturbance source is defined as the signal recorded by the sensor due to the sole action of a particular physical disturbance. Each physical disturbance has its own uniquely generated time signature at a given sensor location. When several sources coexist, the resulting signal, measured by the sensor, is due to the combined effect of all the individual sources and their mutual interactions. Because the actual source-mixing process is usually unknown, it is a challenging task to discern the individual sources from the recorded signal. Source separation, as proposed in this work, is a process aiming at uniquely identifying the disturbance sources and the way they interact. Based on this process, one may relate the individual sources with distinct physical disturbance generators, and, thus, gain useful information about the disturbed flow field. In turn, this information can prove vital in, for example, the design of closed-loop strategies for the control of transitional boundary layers. Moreover, this new approach may provide new insights and perspectives on the way we study transitional flows.
Based on the information acquired by a limited number of sensors, we present a source separation method that can isolate and identify the sources mixed in each sensor measurement. The goal is to provide certain spatial and temporal behaviour characteristics of each source at the location of the sensors. These include the source time signature, propagation velocity and direction in the flow. We focus on disturbances in a boundary layer in which two types of disturbances are linearly superimposed: the first type is Tollmien–Schlichting (TS) waves and the second type is wave packets (WPs). The WP is in fact a superposition of many (theoretically infinite) TS waves. Introducing a disturbance to a boundary layer can cause the flow to transition from laminar to turbulent, through certain scenarios, depending on the disturbance characteristics (Schmid & Henningson Reference Schmid and Henningson2001). In a quiet environment, the early stages of the transition process are governed by linear stability theory (LST), which assumes a linear superposition of the disturbance mixture. In these cases, LST can predict the downstream evolution of the combined disturbances.
Our novel approach of identifying the sources from measured mixtures in shear flow is based on adapting a blind source separation (BSS) technique. Known to be very useful in image processing (Vigario & Oja Reference Vigario and Oja2008; Silva et al. Reference Silva, Figueiredo, Costa and Mascare nas2020), mechanical systems (Antoni Reference Antoni2005; Serviere & Fabry Reference Serviere and Fabry2005; Zhang et al. Reference Zhang, Gao, Liu, Farzadpour, Grebe and Tian2017) and acoustical applications (Sawada, Araki & Makino Reference Sawada, Araki and Makino2010; Yoshioka et al. Reference Yoshioka, Nakatani, Miyoshi and Okuno2010; Nogueira & Petraglia Reference Nogueira and Petraglia2015), BSS methods were originally developed for solving the problem of separating linear convolutive mixtures in acoustic applications, known as the cocktail party problem. In that problem, the goal is to identify the sources of speech pressure waves generated by simultaneously active and independent speakers in the same room (Cherry Reference Cherry1953; Haykin & Chen Reference Haykin and Chen2005). Similar applications can be found in brain imaging data for recovering the original components of brain activity from recorded mixed data, acquired by an electroencephalogram. Source separation has also been applied to astronomical data or satellite images, finding hidden factors in financial data and reducing noise in natural images. For more applications, see Haykin & Chen (Reference Haykin and Chen2005) and Pedersen et al. (Reference Pedersen, Larsen, Kjems and Parra2007) and references therein. Recent developments in BSS methods are based on sparsity-inducing techniques, such as the sparse component extraction algorithm that was proposed by Gao et al. (Reference Gao, Lu, Woo, Tian, Zhu and Johnston2018) for diagnostic imaging systems, and unsupervised data decomposition techniques, such as the non-negative matrix factorization methodology (Ozerov & Fevotte Reference Ozerov and Fevotte2010), and their extensions to three-dimensional non-negative tensor factorization (Cichocki, Zdunek & Amari Reference Cichocki, Zdunek and Amari2007). A broad survey of models and efficient algorithms of non-negative matrix factorization and non-negative tensor factorization for BSS is provided in Cichocki et al. (Reference Cichocki, Zdunek, Phan and Amari2009).
In a recent study by the authors (Gluzman et al. Reference Gluzman, Oshman and Cohen2020), the celebrated independent component analysis (ICA) (Hyvärinen & Oja Reference Hyvärinen and Oja2000) technique was used as a BSS method for the detection and isolation of TS waves in subcritical transitional shear flows based on high-order statistics of the measured signals. The application of the method to measured mixtures from numerical and experimental data has been studied, demonstrating the viability of the method. The efficacy of the method depends on compliance with physics-based sensor placement design rules that resolve the inherent incompatibility between the ICA instantaneous (delay-less) mixture model and the physical mixing process in the considered shear flows. These rules require prior, physics-based, information on the number of sources and the wavelengths of the TS disturbances present in the flow. In turn, this information dictates the required number of sensors, and their relative placement with respect to each other. It is the goal of the present paper to relax the aforementioned structural requirements of the ICA-based method (Hyvärinen & Oja Reference Hyvärinen and Oja2000), thereby extending and fully exploiting the scope of BSS methods to discover and learn about the mixing process of the flow only from available sensor measurements, not requiring any prior information on the sources.
The contributions of this paper are twofold. The first is a method for separating individual disturbance sources that are present in source mixtures measured in a shear boundary layer, using the degenerate unmixing estimation technique (DUET), introduced in Yilmaz & Rickard (Reference Yilmaz and Rickard2004) and Rickard (Reference Rickard2007). Unlike ICA-based BSS techniques, which rely on non-Gaussianity criteria to separate sources, DUET relies on the assumption that the signals are sparse in the time–frequency domain, and was shown to sustain robust performance in noisy environments (Kim et al. Reference Kim, Jang, Jeong and Nam2006; Zhen et al. Reference Zhen, Peng, Yi, Xiang and Chen2017). Characterized by its ability to handle degenerate mixtures, that is, mixtures characterized by fewer sensors than sources, the DUET BSS method is used in this paper to isolate any number of sources using two sensors only, which renders it very efficient relative to other BSS techniques. Exploiting the DUET-based BSS method, the second contribution is a method for determining the propagation velocity vector of each of the identified sources, from measurements acquired by as few as three sensors appropriately placed in the flow field. These two contributions are demonstrated both numerically and experimentally. The numerical study employs LST to model the measured source mixtures acquired by sensors placed in a Blasius boundary layer (BBL). The disturbances that are modelled to be active in the boundary layer are three-dimensional TS waves and WPs, which may propagate downstream in parallel or at a certain angle to the free-stream direction. Carried out in a wind tunnel, the experimental study considers the flow over a flat plate, with hot wires as sensors and a loudspeaker and plasma actuators as source generators.
The remainder of this paper is organized as follows. In § 2 we present the DUET-based BSS method for separating the disturbance sources present in source mixtures acquired by sensors placed in the flow field. Using this DUET-based method, we show in § 3 how to estimate the propagation velocity of disturbances via three sensors appropriately placed in the flow field. Sections 4 and 5 provide numerical and experimental proofs of concept, respectively, for the new methods. Finally, conclusions are drawn in § 6.
2. Blind source separation via DUET
For completeness, we review in this section the main assumptions and procedures for implementing DUET. For more details, the reader is referred to Yilmaz & Rickard (Reference Yilmaz and Rickard2004) and Rickard (Reference Rickard2007).
2.1. Overview of DUET
For blindly separating an arbitrary number of sources with only two provided source mixtures, DUET relies on the following assumptions:
(i) Anechoic mixing model. Originally developed for signal processing in acoustical applications, DUET assumes an anechoic mixing model. Accordingly, the signals of
 $N_s$ mixed sources that are measured by two sensors can be described as
(2.1a)
$N_s$ mixed sources that are measured by two sensors can be described as
(2.1a) \begin{align} x_1(t) & = \sum_{j=1}^{N_s}{s_j(t)}, \end{align}(2.1b)where
\begin{align} x_1(t) & = \sum_{j=1}^{N_s}{s_j(t)}, \end{align}(2.1b)where \begin{align} x_2(t) & =\sum_{j=1}^{N_s}{a_j s_j(t-\delta_j)}, \end{align}
\begin{align} x_2(t) & =\sum_{j=1}^{N_s}{a_j s_j(t-\delta_j)}, \end{align} $x_1(t)$ and
$x_1(t)$ and  $x_2(t)$ are the measurements of sensor 1 and sensor 2, respectively. Here,
$x_2(t)$ are the measurements of sensor 1 and sensor 2, respectively. Here,  $\delta _j$ is the time it takes source
$\delta _j$ is the time it takes source  $s_{j}$ to travel from the location of sensor 1 to the location of sensor 2 and
$s_{j}$ to travel from the location of sensor 1 to the location of sensor 2 and  $a_j$ is the relative attenuation (amplitude growth or decay) of source
$a_j$ is the relative attenuation (amplitude growth or decay) of source  $s_j$ as measured in sensor 2 relative to how it is measured in sensor 1.
$s_j$ as measured in sensor 2 relative to how it is measured in sensor 1.(ii) Windowed-disjoint orthogonality (WDO) of sources. A basic assumption is that the signals are sufficiently sparse so that, at most, one source is dominant at each time–frequency point. In other words, DUET assumes that the sources are disjoint in the time–frequency domain. Mathematically stated, DUET assumes WDO of sources, where the following definition is used: two sources
 $s_j(t)$ and
$s_j(t)$ and  $s_k(t)$ are windowed-disjoint orthogonal if
(2.2)In (2.2),
$s_k(t)$ are windowed-disjoint orthogonal if
(2.2)In (2.2), \begin{equation} \hat{s}_j(\tau,\omega)\hat{s}_k(\tau,\omega)=0, \quad \forall \tau,\omega \text{ and } \forall j\neq k. \end{equation}
\begin{equation} \hat{s}_j(\tau,\omega)\hat{s}_k(\tau,\omega)=0, \quad \forall \tau,\omega \text{ and } \forall j\neq k. \end{equation} $\hat {s}_j(\tau ,\omega )$ is the short-time Fourier transform, or windowed transform, of
$\hat {s}_j(\tau ,\omega )$ is the short-time Fourier transform, or windowed transform, of  $s_j(t)$, defined as
(2.3)where
$s_j(t)$, defined as
(2.3)where \begin{equation} \hat{s}_j(\tau,\omega) = \mathcal{F}^W[s_j](\tau,\omega) \triangleq \frac{1}{2{\rm \pi}}\int_{-\infty}^{\infty}W(t-\tau)s_j(t)\ \textrm{e}^{-\textrm{i}\omega t}\,\textrm{d}t, \end{equation}
\begin{equation} \hat{s}_j(\tau,\omega) = \mathcal{F}^W[s_j](\tau,\omega) \triangleq \frac{1}{2{\rm \pi}}\int_{-\infty}^{\infty}W(t-\tau)s_j(t)\ \textrm{e}^{-\textrm{i}\omega t}\,\textrm{d}t, \end{equation} $W(t-\tau )$ is the Hann window function centred at
$W(t-\tau )$ is the Hann window function centred at  $\tau$,
$\tau$,  $\omega =2{\rm \pi} f$ where
$\omega =2{\rm \pi} f$ where  $f$ is the frequency (having the units of
$f$ is the frequency (having the units of  $\tau ^{-1}$) and
$\tau ^{-1}$) and  $\textrm {i}=\sqrt {-1}$.
$\textrm {i}=\sqrt {-1}$.(iii) Local stationarity. The DUET algorithm assumes that, for a given sensor spatial separation (see next assumption), source propagation speed and selected time window, the sources comprising the measured mixtures are locally stationary, i.e. they satisfy
(2.4)where \begin{equation} \mathcal{F}^W[s_j(t-\delta_j)](\tau,\omega) = \textrm{e}^{-\textrm{i}\omega\delta_j}\mathcal{F}^W[s_j(t)](\tau,\omega), \quad \forall \delta_j \text{ such that } |\delta_j|<\varDelta, \end{equation}
\begin{equation} \mathcal{F}^W[s_j(t-\delta_j)](\tau,\omega) = \textrm{e}^{-\textrm{i}\omega\delta_j}\mathcal{F}^W[s_j(t)](\tau,\omega), \quad \forall \delta_j \text{ such that } |\delta_j|<\varDelta, \end{equation} $\varDelta$ is the maximum possible time difference in the mixing model. The time difference
$\varDelta$ is the maximum possible time difference in the mixing model. The time difference  $\varDelta$ can be obtained by dividing the distance between the sensors by the slowest source propagation speed.
$\varDelta$ can be obtained by dividing the distance between the sensors by the slowest source propagation speed.(iv) Sensor spatial separation. DUET estimates the delay
 $\delta _j$ from the
$\delta _j$ from the  $\textrm {e}^{-\textrm {i}\omega \delta _j}$ term (this is shown next). There are infinitely many possible estimates of
$\textrm {e}^{-\textrm {i}\omega \delta _j}$ term (this is shown next). There are infinitely many possible estimates of  $\delta _j$ based on that term, all satisfying
$\delta _j$ based on that term, all satisfying  $\delta _j=\delta +2{\rm \pi} k$ for
$\delta _j=\delta +2{\rm \pi} k$ for  $k \in \mathbb {Z}$ (this integer ambiguity is also called the wrap-around problem). To circumvent this problem without having to solve for the unknown integer delays, it is assumed that the distance between sensors,
$k \in \mathbb {Z}$ (this integer ambiguity is also called the wrap-around problem). To circumvent this problem without having to solve for the unknown integer delays, it is assumed that the distance between sensors,  $\Delta r$, is sufficiently small, so as to guarantee a unique solution. We thus require
(2.5)which leads to the following condition on the distance between sensors:
$\Delta r$, is sufficiently small, so as to guarantee a unique solution. We thus require
(2.5)which leads to the following condition on the distance between sensors: \begin{equation} |\omega\delta_j|<{\rm \pi}, \quad \forall \omega \text{ and } \forall j, \end{equation}(2.6)where
\begin{equation} |\omega\delta_j|<{\rm \pi}, \quad \forall \omega \text{ and } \forall j, \end{equation}(2.6)where \begin{equation} \Delta r<\frac{{\rm \pi} U}{\omega_m}, \end{equation}
\begin{equation} \Delta r<\frac{{\rm \pi} U}{\omega_m}, \end{equation} $\omega _m$ is the maximum frequency present in the mixture and
$\omega _m$ is the maximum frequency present in the mixture and  $U$ is the speed of the slowest disturbance source in the mixture. This constraint can be removed using various DUET extensions, as proposed by Rickard (Reference Rickard2007) and Wang, Yılmaz & Zhou (Reference Wang, Yılmaz and Zhou2013).
$U$ is the speed of the slowest disturbance source in the mixture. This constraint can be removed using various DUET extensions, as proposed by Rickard (Reference Rickard2007) and Wang, Yılmaz & Zhou (Reference Wang, Yılmaz and Zhou2013).(v) Signal signature diversity. If two sources have identical spatial signatures, that is, identical relative attenuations and relative delays (mixing parameters), then they can be combined into one source without changing the model, rendering them inseparable by DUET. We thus assume that
(2.7) \begin{equation} (a_j\neq a_k) \text{ or } (\delta_j\neq \delta_k), \quad\forall j\neq k. \end{equation}
\begin{equation} (a_j\neq a_k) \text{ or } (\delta_j\neq \delta_k), \quad\forall j\neq k. \end{equation}
Assumptions (i)–(iii) yield
The WDO assumption means that only a single source ![]() $s_j$ can be active at a certain point
$s_j$ can be active at a certain point ![]() $(\tau ,\omega )$ in the time–frequency domain. In the interest of practicality, we relax this assumption and require, alternatively, that if several sources are active at the same time–frequency point, then one of them is dominant, in the sense that it can be regarded as the single active source at that time–frequency point. Dividing
$(\tau ,\omega )$ in the time–frequency domain. In the interest of practicality, we relax this assumption and require, alternatively, that if several sources are active at the same time–frequency point, then one of them is dominant, in the sense that it can be regarded as the single active source at that time–frequency point. Dividing ![]() ${\hat x}_2$ by
${\hat x}_2$ by ![]() ${\hat x}_1$ in (2.8), we thus obtain
${\hat x}_1$ in (2.8), we thus obtain
where ![]() $\varOmega _j$ is defined as the set of time–frequency pairs
$\varOmega _j$ is defined as the set of time–frequency pairs ![]() $(\tau ,\omega )$ for which the sources are sufficiently sparse so that, at most, one of them is dominant at each time–frequency combination, i.e.
$(\tau ,\omega )$ for which the sources are sufficiently sparse so that, at most, one of them is dominant at each time–frequency combination, i.e.
The important result of (2.9) is that the ratio of the short-time Fourier transformed signals, ![]() ${{{\hat x}_2}(\tau ,\omega )} / {{{\hat x}_1}(\tau ,\omega )}$, does not depend on the signals themselves, but on their mixing parameters
${{{\hat x}_2}(\tau ,\omega )} / {{{\hat x}_1}(\tau ,\omega )}$, does not depend on the signals themselves, but on their mixing parameters ![]() $a_j$ and
$a_j$ and ![]() $\delta _j$ only. In DUET, the sources
$\delta _j$ only. In DUET, the sources ![]() $s_j$ are identified via estimation of
$s_j$ are identified via estimation of ![]() $a_j$ and
$a_j$ and ![]() $\delta _j$. This is done by local estimation of the mixing parameters,
$\delta _j$. This is done by local estimation of the mixing parameters, ![]() $\tilde a$ and
$\tilde a$ and ![]() $\tilde \delta$, for each time–frequency pair
$\tilde \delta$, for each time–frequency pair ![]() $(\tau , \omega )$ and a combination of the set of local mixing-parameter estimates into
$(\tau , \omega )$ and a combination of the set of local mixing-parameter estimates into ![]() $N_s$ pairings corresponding to the true mixing-parameter pairings. From (2.9), for each time–frequency point
$N_s$ pairings corresponding to the true mixing-parameter pairings. From (2.9), for each time–frequency point ![]() $(\tau , \omega )$, we obtain local estimates of the relative delay,
$(\tau , \omega )$, we obtain local estimates of the relative delay, ![]() $\tilde \delta (\tau ,\omega )$, and the relative attenuation,
$\tilde \delta (\tau ,\omega )$, and the relative attenuation, ![]() $\tilde a(\tau ,\omega )$, as
$\tilde a(\tau ,\omega )$, as
For convenience, the relative attenuation ![]() $\tilde a$ is replaced by the symmetric relative attenuation
$\tilde a$ is replaced by the symmetric relative attenuation ![]() $\tilde \alpha$:
$\tilde \alpha$:
According to (2.13), ![]() $\tilde \alpha$ changes sign when sensors are swapped. Under assumptions (iv) and (v), the local symmetric relative attenuation and delay estimates,
$\tilde \alpha$ changes sign when sensors are swapped. Under assumptions (iv) and (v), the local symmetric relative attenuation and delay estimates, ![]() $\tilde \alpha (\tau ,\omega )$ and
$\tilde \alpha (\tau ,\omega )$ and ![]() $\tilde \delta (\tau ,\omega )$, respectively, should be related to the actual
$\tilde \delta (\tau ,\omega )$, respectively, should be related to the actual ![]() $\alpha _j(\tau ,\omega )$ and
$\alpha _j(\tau ,\omega )$ and ![]() $\delta _j(\tau ,\omega )$ of each source
$\delta _j(\tau ,\omega )$ of each source ![]() $s_j$. In other words, the union of the
$s_j$. In other words, the union of the ![]() $(\tilde \alpha (\tau ,\omega ), \tilde \delta (\tau ,\omega ))$ pairs, taken over all (
$(\tilde \alpha (\tau ,\omega ), \tilde \delta (\tau ,\omega ))$ pairs, taken over all (![]() $\tau ,\omega$) combinations, is the set of
$\tau ,\omega$) combinations, is the set of ![]() $N_s$
$N_s$ ![]() $(\alpha _j, \delta _j)$ pairs:
$(\alpha _j, \delta _j)$ pairs:
For source separation, binary masks are generated by
 \begin{equation} M_j(\tau,\omega ) =\begin{cases} 1 & ( \tilde a(\tau,\omega ),\tilde \delta (\tau,\omega ) ) =(a_j,\delta _j), \\ 0 & \text{otherwise}. \end{cases} \end{equation}
\begin{equation} M_j(\tau,\omega ) =\begin{cases} 1 & ( \tilde a(\tau,\omega ),\tilde \delta (\tau,\omega ) ) =(a_j,\delta _j), \\ 0 & \text{otherwise}. \end{cases} \end{equation}Finally, the separation of sources is obtained by multiplying each mask with one of the mixtures.
2.2. Implementation of DUET
The implementation of DUET is based on transforming (2.14) and (2.15) to operational relations. In Yilmaz & Rickard (Reference Yilmaz and Rickard2004), it was found that in the approximate WDO case, the instantaneous DUET estimates ![]() $\tilde a(\tau ,\omega ), \tilde \delta (\tau ,\omega )$ (equations (2.11) and (2.13)) are not identically related to the actual mixing parameters
$\tilde a(\tau ,\omega ), \tilde \delta (\tau ,\omega )$ (equations (2.11) and (2.13)) are not identically related to the actual mixing parameters ![]() $(\alpha _j, \delta _j)$ of the original
$(\alpha _j, \delta _j)$ of the original ![]() $N_s$ sources, but they cluster around them. Therefore, the realization of (2.14) is obtained by construction of a two-dimensional weighted histogram for determining these clusters. The histogram domain,
$N_s$ sources, but they cluster around them. Therefore, the realization of (2.14) is obtained by construction of a two-dimensional weighted histogram for determining these clusters. The histogram domain, ![]() $I(\alpha ,\delta )$, is defined over
$I(\alpha ,\delta )$, is defined over ![]() $\tilde a(\tau ,\omega ), \tilde \delta (\tau ,\omega )$ as follows:
$\tilde a(\tau ,\omega ), \tilde \delta (\tau ,\omega )$ as follows:
where ![]() $\varDelta _\alpha$ and
$\varDelta _\alpha$ and ![]() $\varDelta _\delta$ are smoothing resolution widths. Using the
$\varDelta _\delta$ are smoothing resolution widths. Using the ![]() $\tilde a(\tau , \omega ), \tilde \delta (\tau , \omega )$ pairs to indicate the indices of the histogram and using
$\tilde a(\tau , \omega ), \tilde \delta (\tau , \omega )$ pairs to indicate the indices of the histogram and using ![]() $|{\hat x}_1(\tau , \omega ){\hat x}_2(\tau , \omega ) |^p \omega ^q$ for the weight, a two-dimensional weighted histogram is constructed:
$|{\hat x}_1(\tau , \omega ){\hat x}_2(\tau , \omega ) |^p \omega ^q$ for the weight, a two-dimensional weighted histogram is constructed:
Here, ![]() $p$ and
$p$ and ![]() $q$ are variables of a weighted average, which, by default, are set to
$q$ are variables of a weighted average, which, by default, are set to ![]() $p = 1$,
$p = 1$, ![]() $q = 0$ (Yilmaz & Rickard Reference Yilmaz and Rickard2004). If assumptions (i)–(v) hold, (2.17) takes the form
$q = 0$ (Yilmaz & Rickard Reference Yilmaz and Rickard2004). If assumptions (i)–(v) hold, (2.17) takes the form
 \begin{equation} H(\alpha,\delta) =\begin{cases} \displaystyle\iint_{(\tau, \omega ) \in I( {\alpha, \delta } )} | {\hat s}_j(\tau, \omega ) |^{2p}{\omega ^q}\,\textrm{d}\tau \,\textrm{d}\omega & | \alpha _j - \alpha| < \varDelta _\alpha, \ | \delta _j - \delta |<\varDelta _\delta, \\ 0 & \text{otherwise}. \end{cases} \end{equation}
\begin{equation} H(\alpha,\delta) =\begin{cases} \displaystyle\iint_{(\tau, \omega ) \in I( {\alpha, \delta } )} | {\hat s}_j(\tau, \omega ) |^{2p}{\omega ^q}\,\textrm{d}\tau \,\textrm{d}\omega & | \alpha _j - \alpha| < \varDelta _\alpha, \ | \delta _j - \delta |<\varDelta _\delta, \\ 0 & \text{otherwise}. \end{cases} \end{equation}
The weighted histogram separates and clusters the parameter estimates of each source. The number of peaks reveals the number of sources, and the peak locations reveal the associated source's anechoic mixing parameters, which are denoted by ![]() $(\tilde \alpha _j, \tilde \delta _j)$. Then, the relative estimated attenuation
$(\tilde \alpha _j, \tilde \delta _j)$. Then, the relative estimated attenuation ![]() $\tilde a_j$ is retrieved from the estimated symmetric attenuation
$\tilde a_j$ is retrieved from the estimated symmetric attenuation ![]() $\tilde \alpha _j$ by
$\tilde \alpha _j$ by
 \begin{equation} \tilde a_j = \frac{ {\tilde \alpha}_j + \sqrt {{\tilde \alpha }_j^2 + 4} }{2}. \end{equation}
\begin{equation} \tilde a_j = \frac{ {\tilde \alpha}_j + \sqrt {{\tilde \alpha }_j^2 + 4} }{2}. \end{equation}
Next, ![]() $N_s$ estimated pairs
$N_s$ estimated pairs ![]() $(\tilde \alpha _j, \tilde \delta _j)$ should be related back to each time–frequency point
$(\tilde \alpha _j, \tilde \delta _j)$ should be related back to each time–frequency point ![]() $(\tau ,\omega )$ which is closest to the local parameter estimates
$(\tau ,\omega )$ which is closest to the local parameter estimates ![]() $(\tilde \alpha (\tau ,\omega ), \tilde \delta (\tau ,\omega ))$. Following Yilmaz & Rickard (Reference Yilmaz and Rickard2004), a maximum-likelihood association rule (estimator) for the
$(\tilde \alpha (\tau ,\omega ), \tilde \delta (\tau ,\omega ))$. Following Yilmaz & Rickard (Reference Yilmaz and Rickard2004), a maximum-likelihood association rule (estimator) for the ![]() $j$th source is obtained as
$j$th source is obtained as
 \begin{equation} J(\tau, \omega )\triangleq \arg\min_j \frac{ | {\tilde a}_j \ \textrm{e}^{ - \textrm{i} {\tilde \delta }_j \omega }{\hat x}_1(\tau, \omega ) - {\hat x}_2(\tau, \omega ) |^2 }{ 1 + {\tilde a}_j^2 }. \end{equation}
\begin{equation} J(\tau, \omega )\triangleq \arg\min_j \frac{ | {\tilde a}_j \ \textrm{e}^{ - \textrm{i} {\tilde \delta }_j \omega }{\hat x}_1(\tau, \omega ) - {\hat x}_2(\tau, \omega ) |^2 }{ 1 + {\tilde a}_j^2 }. \end{equation}
These obtained estimators are used to obtain ![]() $N_s$ binary masks, as follows:
$N_s$ binary masks, as follows:
 \begin{equation} {\tilde M}_j(\tau,\omega) =\begin{cases} 1 & J(\tau, \omega) = j, \\ 0 & \text{otherwise}, \end{cases} \end{equation}
\begin{equation} {\tilde M}_j(\tau,\omega) =\begin{cases} 1 & J(\tau, \omega) = j, \\ 0 & \text{otherwise}, \end{cases} \end{equation}
and the maximum-likelihood source estimates are obtained, as proposed in Yilmaz & Rickard (Reference Yilmaz and Rickard2004), based on maximum-likelihood estimates of ![]() $(\tilde \alpha _j, \tilde \delta _j)$, as
$(\tilde \alpha _j, \tilde \delta _j)$, as
 \begin{equation} \hat{s}_j(\tau, \omega ) = {\tilde M}_j(\tau, \omega )\frac{ {\hat x}_1(\tau, \omega) + {\tilde a}_j \ \textrm{e}^{\textrm{i}{\tilde \delta}_j\omega}{\hat x}_2(\tau, \omega) }{ 1 + {\tilde a}_j^2 }. \end{equation}
\begin{equation} \hat{s}_j(\tau, \omega ) = {\tilde M}_j(\tau, \omega )\frac{ {\hat x}_1(\tau, \omega) + {\tilde a}_j \ \textrm{e}^{\textrm{i}{\tilde \delta}_j\omega}{\hat x}_2(\tau, \omega) }{ 1 + {\tilde a}_j^2 }. \end{equation}In summary, implementing DUET consists of the following main steps (we assume that two mixtures are acquired):
(i) Construct time–frequency representations of both mixtures:
 $\hat {x}_1(\tau ,\omega )$,
$\hat {x}_1(\tau ,\omega )$,  $\hat {x}_2(\tau ,\omega )$.
$\hat {x}_2(\tau ,\omega )$.(ii) Extract local mixing-parameter estimates:
 $\tilde {a}(\tau ,\omega )$,
$\tilde {a}(\tau ,\omega )$,  $\tilde {\delta }(\tau ,\omega )$.
$\tilde {\delta }(\tau ,\omega )$.(iii) Out of the set of local mixing-parameter estimates, form
 $N_s$ parameter pairings, optimally corresponding to the true mixing-parameter pairings:
$N_s$ parameter pairings, optimally corresponding to the true mixing-parameter pairings:  $(\tilde {a}_1, \tilde {\delta }_1), \ldots , (\tilde {a}_{N_s}, \tilde {\delta }_{N_s})$.
$(\tilde {a}_1, \tilde {\delta }_1), \ldots , (\tilde {a}_{N_s}, \tilde {\delta }_{N_s})$.(iv) For each determined mixing-parameter pair, generate a binary mask corresponding to the time–frequency points that yield that particular mixing-parameter pair:
 $M_1(\tau ,\omega ), \ldots , M_{N_s}(\tau ,\omega )$.
$M_1(\tau ,\omega ), \ldots , M_{N_s}(\tau ,\omega )$.(v) Isolate (demix) the sources by applying each mask to both mixtures. This yields:
 $\hat {s}_{1}(\tau ,\omega ),\ldots ,\hat {s}_{N_s}(\tau ,\omega )$.
$\hat {s}_{1}(\tau ,\omega ),\ldots ,\hat {s}_{N_s}(\tau ,\omega )$.(vi) Finally, transform each demixed time–frequency representation to the time domain, yielding the isolated sources
 $s_{1}(t), \ldots , s_{N_s}(t)$.
$s_{1}(t), \ldots , s_{N_s}(t)$.
In the following we extend the DUET-based method to also determine the propagation velocity vector of each of the identified sources.
3. Estimation of disturbance propagation velocity via DUET
The method proposed herein for determining the source propagation velocity (direction and speed) is based on sampling the flow in several different locations and then using the DUET method on these samples. Regarding a particular sensor, each source is characterized by two parameters: (1) the direction from which the source is arriving and (2) its distance relative to the sensor. Let ![]() $\delta _{ikj}$ denote the relative delay of arrival of a specific source
$\delta _{ikj}$ denote the relative delay of arrival of a specific source ![]() $s_j$, between two sensors,
$s_j$, between two sensors, ![]() $x_i$ and
$x_i$ and ![]() $x_k$. We define
$x_k$. We define ![]() $\delta _{ikj}$ to be positive if the source first arrives at sensor
$\delta _{ikj}$ to be positive if the source first arrives at sensor ![]() $x_i$ and then at
$x_i$ and then at ![]() $x_k$, and negative vice versa. Thus, the sign of
$x_k$, and negative vice versa. Thus, the sign of ![]() $\delta _{ijk}$ (by itself) provides a partial indication of the source direction. The observation underlying the method presented in this section is that the DUET algorithm can provide an estimate of
$\delta _{ijk}$ (by itself) provides a partial indication of the source direction. The observation underlying the method presented in this section is that the DUET algorithm can provide an estimate of ![]() $\delta _{ikj}$. This estimate can, in turn, be used to estimate the propagation direction of the source.
$\delta _{ikj}$. This estimate can, in turn, be used to estimate the propagation direction of the source.
Assuming three sensors, the geometrical model of the source propagation direction determination problem is schematically depicted in figure 1. In addition to the assumptions used to blindly separate the sources using DUET, we add the following three assumptions:
(i) Each source is assumed to possess a uniform planar wave front, i.e. the source wave front's curvature is neglected.
(ii) The dispersive nature of a WP source is neglected, so that its group velocity is taken to represent the velocity of the source.
(iii) The sensors are assumed to be omni-directional, i.e. capable of measuring sources arriving from any direction.

Figure 1. Measurement geometry of a source with velocity ![]() $\boldsymbol {u}$. Three sensors are used.
$\boldsymbol {u}$. Three sensors are used.
These assumptions generally hold for disturbances in transitional flows. In particular, the first assumption is valid if the source is formed sufficiently far away from the sensors, which means that, compared with the distances between the sensors, the distance between the point of creation of the source and the sensors is large. The second assumption is valid for WP sources if the sensors are placed close to each other (which can be regarded as a design constraint). Being somewhat more restrictive, the third assumption does not strictly hold for a single hot-wire sensor, measuring the fluid velocity component perpendicular to the hot wire. Nevertheless, as is demonstrated in what follows, even flow components arriving at oblique angles to the wire can still be captured, albeit at an attenuated level.
3.1. Method derivation
Our approach for source propagation direction determination derives from that of Oshman & Markley (Reference Oshman and Markley1999), where a global positioning system (GPS) antenna array is used for spacecraft attitude estimation, based on measuring the phase difference between GPS signals acquired by the antenna array.
Consider a source ![]() $s$ that propagates in the
$s$ that propagates in the ![]() $x$–
$x$–![]() $z$ plane with velocity
$z$ plane with velocity
where the source speed is ![]() $u= | {\boldsymbol {u}}|$ and
$u= | {\boldsymbol {u}}|$ and ![]() $\hat { {\boldsymbol {u}}}$ is a unit directional vector. Our goal is to determine this velocity (both direction and magnitude) for each source from source mixtures measured by
$\hat { {\boldsymbol {u}}}$ is a unit directional vector. Our goal is to determine this velocity (both direction and magnitude) for each source from source mixtures measured by ![]() $N$ sensors.
$N$ sensors.
We position ![]() $N$ sensors in the flow located at
$N$ sensors in the flow located at ![]() $\boldsymbol {r}_{x_{i}}$,
$\boldsymbol {r}_{x_{i}}$, ![]() $i=1, \ldots , N$, in the
$i=1, \ldots , N$, in the ![]() $x$–
$x$–![]() $z$ plane (
$z$ plane (![]() $N=3$ in figure 1). Analogously to the GPS antenna array of Oshman & Markley (Reference Oshman and Markley1999), we denote sensor 1 as the master sensor and, accordingly, sensors
$N=3$ in figure 1). Analogously to the GPS antenna array of Oshman & Markley (Reference Oshman and Markley1999), we denote sensor 1 as the master sensor and, accordingly, sensors ![]() $2,\ldots , N$ as the slave sensors. This sensor array configuration defines
$2,\ldots , N$ as the slave sensors. This sensor array configuration defines ![]() $N-1$ baseline vectors,
$N-1$ baseline vectors, ![]() $\boldsymbol {r}_{x_{i}} - \boldsymbol {r}_{x_{1}}$,
$\boldsymbol {r}_{x_{i}} - \boldsymbol {r}_{x_{1}}$, ![]() $i=2, \ldots , N$. As in GPS attitude determination problems, here, too, a minimum of two baselines are required, corresponding to a minimal configuration of three sensors.
$i=2, \ldots , N$. As in GPS attitude determination problems, here, too, a minimum of two baselines are required, corresponding to a minimal configuration of three sensors.
The source ![]() $s$ that travels from the master sensor (sensor 1) to slave sensor
$s$ that travels from the master sensor (sensor 1) to slave sensor ![]() $i$,
$i$, ![]() $i=2, \ldots , N$, covers the distance
$i=2, \ldots , N$, covers the distance
where we have used a shorthand notation for the delay ![]() $\delta _i$, and
$\delta _i$, and ![]() $\delta _{i} > 0$ (
$\delta _{i} > 0$ (![]() $\delta _{i} < 0$ with the same magnitude if the source travels in the opposite direction). We now use the normalized baseline vectors to define the rows of the matrix
$\delta _{i} < 0$ with the same magnitude if the source travels in the opposite direction). We now use the normalized baseline vectors to define the rows of the matrix ![]() ${\boldsymbol{\mathsf{W}}} \in \mathbb {R}^{N-1,2}$:
${\boldsymbol{\mathsf{W}}} \in \mathbb {R}^{N-1,2}$:
 \begin{equation} {\boldsymbol{\mathsf{W}}} \triangleq \begin{bmatrix} \delta_{2}^{{-}1} (\boldsymbol{r}_{x_{2}} - \boldsymbol{r}_{x_{1}})^\textrm{T} \\ \delta_{3}^{{-}1} (\boldsymbol{r}_{x_{3}} - \boldsymbol{r}_{x_{1}})^\textrm{T}\\ \vdots\\ \delta_{N}^{{-}1} (\boldsymbol{r}_{x_{N}} - \boldsymbol{r}_{x_{1}})^\textrm{T} \end{bmatrix}. \end{equation}
\begin{equation} {\boldsymbol{\mathsf{W}}} \triangleq \begin{bmatrix} \delta_{2}^{{-}1} (\boldsymbol{r}_{x_{2}} - \boldsymbol{r}_{x_{1}})^\textrm{T} \\ \delta_{3}^{{-}1} (\boldsymbol{r}_{x_{3}} - \boldsymbol{r}_{x_{1}})^\textrm{T}\\ \vdots\\ \delta_{N}^{{-}1} (\boldsymbol{r}_{x_{N}} - \boldsymbol{r}_{x_{1}})^\textrm{T} \end{bmatrix}. \end{equation}Then, (3.2) can be rewritten as
where all entries of the vector ![]() $ {\boldsymbol {1}} \in \mathbb {R}^{N-1}$ are ones. Equation (3.4) is a system of
$ {\boldsymbol {1}} \in \mathbb {R}^{N-1}$ are ones. Equation (3.4) is a system of ![]() $N-1$ linear equations for the speed
$N-1$ linear equations for the speed ![]() $u_{}$ and the independent entry of the direction vector
$u_{}$ and the independent entry of the direction vector ![]() $\hat {\boldsymbol {u}}_{}$. For
$\hat {\boldsymbol {u}}_{}$. For ![]() $N=3$, this system has a unique solution if the columns of
$N=3$, this system has a unique solution if the columns of ![]() ${\boldsymbol{\mathsf{W}}}$ are independent, which corresponds to a three-sensor configuration having two non-collinear baselines. For
${\boldsymbol{\mathsf{W}}}$ are independent, which corresponds to a three-sensor configuration having two non-collinear baselines. For ![]() $N>3$, the system becomes overdetermined, calling for a least squares solution, a minimum-norm version of which is provided by the Moore–Penrose pseudoinverse of
$N>3$, the system becomes overdetermined, calling for a least squares solution, a minimum-norm version of which is provided by the Moore–Penrose pseudoinverse of ![]() ${\boldsymbol{\mathsf{W}}}$, which can be robustly computed using the singular value decomposition.
${\boldsymbol{\mathsf{W}}}$, which can be robustly computed using the singular value decomposition.
3.2. Sensor configuration design
Relative to some given disturbance direction, the configuration of the ![]() $N$ sensors determines the numerical properties of the linear system (3.4), which, in turn, determine the quality of the solution for the disturbance propagation velocity. We use the condition number of the coefficient matrix, denoted as
$N$ sensors determines the numerical properties of the linear system (3.4), which, in turn, determine the quality of the solution for the disturbance propagation velocity. We use the condition number of the coefficient matrix, denoted as ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}$, which is the ratio between the largest and smallest singular values of
${\kappa ({\boldsymbol{\mathsf{W}}})}$, which is the ratio between the largest and smallest singular values of ![]() ${\boldsymbol{\mathsf{W}}}$, as a measure of the quality of the solution. A small condition number, i.e. a condition number close to one, means that the system is well-conditioned, and a high-quality solution may be expected. On the other hand, a large condition number is associated with an ill-conditioned system, leading to a solution of poor quality, due to system sensitivity to small input errors.
${\boldsymbol{\mathsf{W}}}$, as a measure of the quality of the solution. A small condition number, i.e. a condition number close to one, means that the system is well-conditioned, and a high-quality solution may be expected. On the other hand, a large condition number is associated with an ill-conditioned system, leading to a solution of poor quality, due to system sensitivity to small input errors.
Evaluating the condition number as a function of the sensor configuration and disturbance direction can naturally assist in the following two sensor design tasks:
(i) Given a certain sensor configuration,
 ${\kappa ({\boldsymbol{\mathsf{W}}})}$ can be used to find the unobservable directions; that is, the disturbance directions that cannot be identified using the given configuration.
${\kappa ({\boldsymbol{\mathsf{W}}})}$ can be used to find the unobservable directions; that is, the disturbance directions that cannot be identified using the given configuration.(ii) Given the disturbance direction,
 ${\kappa ({\boldsymbol{\mathsf{W}}})}$ can be used to design the best sensor configuration for the task of disturbance velocity estimation.
${\kappa ({\boldsymbol{\mathsf{W}}})}$ can be used to design the best sensor configuration for the task of disturbance velocity estimation.
In what follows, we demonstrate the above two tasks via illustrative examples.
3.2.1. Unobservable directions for a given sensor configuration
In this subsection, we demonstrate how the ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}$ measure may assist in finding the unobservable directions associated with a given three-sensor configuration. The disturbance speed is set to be
${\kappa ({\boldsymbol{\mathsf{W}}})}$ measure may assist in finding the unobservable directions associated with a given three-sensor configuration. The disturbance speed is set to be ![]() $| {\boldsymbol {u}}|=1$ m s
$| {\boldsymbol {u}}|=1$ m s![]() $^{-1}$ and the velocity direction, represented by the angle
$^{-1}$ and the velocity direction, represented by the angle ![]() $\theta$ with respect to
$\theta$ with respect to ![]() $\hat { {\boldsymbol {e}}}_x$ as displayed in figure 1, is varied between 0
$\hat { {\boldsymbol {e}}}_x$ as displayed in figure 1, is varied between 0![]() $^\circ$ and 360
$^\circ$ and 360![]() $^\circ$ at 4001 points uniformly spread in this range.
$^\circ$ at 4001 points uniformly spread in this range.
In the top three panels of figure 2, we illustrate three different three-sensor configurations, all consisting of a master sensor 1 (marked by the symbol ![]() $\times$) and two slave sensors 2 and 3 (marked as small circle and square, respectively). The two baselines are illustrated by arrows, pointing from the master sensor to the slave sensors. The bottom three panels of figure 2 present the value of the
$\times$) and two slave sensors 2 and 3 (marked as small circle and square, respectively). The two baselines are illustrated by arrows, pointing from the master sensor to the slave sensors. The bottom three panels of figure 2 present the value of the ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}$ measure on polar coordinates as a function of
${\kappa ({\boldsymbol{\mathsf{W}}})}$ measure on polar coordinates as a function of ![]() $\theta$, the disturbance arrival direction. The radial distance from the origin stands for the value of
$\theta$, the disturbance arrival direction. The radial distance from the origin stands for the value of ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}$, and the two circles in each of these plots correspond to the values of
${\kappa ({\boldsymbol{\mathsf{W}}})}$, and the two circles in each of these plots correspond to the values of ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}=2.5$ (inner dotted circle) and
${\kappa ({\boldsymbol{\mathsf{W}}})}=2.5$ (inner dotted circle) and ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}=5$ (outer circle). Disturbance arrival angles corresponding to
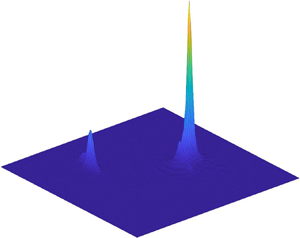
${\kappa ({\boldsymbol{\mathsf{W}}})}=5$ (outer circle). Disturbance arrival angles corresponding to ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})} \ge 50$ are marked in these plots by red arcs on the outer circle. The ill-conditioning threshold value of 50 is arbitrarily chosen; clearly, disturbance sources arriving from directions corresponding to angles within the red arcs may not be determined correctly. As may be expected, figure 2(c) reveals that when the two baselines are collinear, the entire polar domain is unobservable.
${\kappa ({\boldsymbol{\mathsf{W}}})} \ge 50$ are marked in these plots by red arcs on the outer circle. The ill-conditioning threshold value of 50 is arbitrarily chosen; clearly, disturbance sources arriving from directions corresponding to angles within the red arcs may not be determined correctly. As may be expected, figure 2(c) reveals that when the two baselines are collinear, the entire polar domain is unobservable.

Figure 2. Unobservable directions for (a–c) three sensor configurations. Top panels: sensor configurations. Master sensor marked by ![]() $\times$, slave sensors marked by circle and square symbols, baselines denoted by arrows. Bottom panels: polar plots of
$\times$, slave sensors marked by circle and square symbols, baselines denoted by arrows. Bottom panels: polar plots of ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}$ versus disturbance arrival direction. Angles associated with
${\kappa ({\boldsymbol{\mathsf{W}}})}$ versus disturbance arrival direction. Angles associated with ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})} \ge 50$ are shown via red arcs on the outer circles (that correspond to
${\kappa ({\boldsymbol{\mathsf{W}}})} \ge 50$ are shown via red arcs on the outer circles (that correspond to ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}=5$).
${\kappa ({\boldsymbol{\mathsf{W}}})}=5$).
3.2.2. Best sensor configuration for a given disturbance direction
We next demonstrate how the ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}$ measure is used to design the optimal sensor configuration for a given disturbance direction. The disturbance speed is set to
${\kappa ({\boldsymbol{\mathsf{W}}})}$ measure is used to design the optimal sensor configuration for a given disturbance direction. The disturbance speed is set to ![]() $| {\boldsymbol {u}}_j| =1$ m s
$| {\boldsymbol {u}}_j| =1$ m s![]() $^{-1}$ and the disturbance arrival angle varies between (a)
$^{-1}$ and the disturbance arrival angle varies between (a) ![]() $\theta = -90^\circ$, (b)
$\theta = -90^\circ$, (b) ![]() $\theta = -60^\circ$, (c)
$\theta = -60^\circ$, (c) ![]() $\theta = -20^\circ$ and (d)
$\theta = -20^\circ$ and (d) ![]() $\theta = 0^\circ$. Two sensors are fixed, whereas the location of the third sensor varies within the range
$\theta = 0^\circ$. Two sensors are fixed, whereas the location of the third sensor varies within the range ![]() $x,z \in [-50, 50]$ mm, with 1 mm step in each direction. Figure 3 displays the value of
$x,z \in [-50, 50]$ mm, with 1 mm step in each direction. Figure 3 displays the value of ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}$ for all possible locations of the third sensor in the
${\kappa ({\boldsymbol{\mathsf{W}}})}$ for all possible locations of the third sensor in the ![]() $x$–
$x$–![]() $z$ plane. Regions of the
$z$ plane. Regions of the ![]() $x$–
$x$–![]() $z$ plane associated with high values of
$z$ plane associated with high values of ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}$ should be avoided. In figure 3(d), the first slave sensor is located such that its baseline is perpendicular to the disturbance velocity vector, which results in
${\kappa ({\boldsymbol{\mathsf{W}}})}$ should be avoided. In figure 3(d), the first slave sensor is located such that its baseline is perpendicular to the disturbance velocity vector, which results in ![]() $\delta _{12}= 0$. Therefore,
$\delta _{12}= 0$. Therefore, ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})} \to \infty$ for any location of the second slave sensor, rendering the determination of the velocity vector in this configuration impossible. In general, figure 3(d) demonstrates that the problem becomes unobservable if the sensors are configured such that either (1) at least one baseline is perpendicular to the disturbance velocity vector or (2) the baselines are collinear.
${\kappa ({\boldsymbol{\mathsf{W}}})} \to \infty$ for any location of the second slave sensor, rendering the determination of the velocity vector in this configuration impossible. In general, figure 3(d) demonstrates that the problem becomes unobservable if the sensors are configured such that either (1) at least one baseline is perpendicular to the disturbance velocity vector or (2) the baselines are collinear.

Figure 3. The ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}$ measure as a function of the location of the third sensor, when the first two sensors (marked by the
${\kappa ({\boldsymbol{\mathsf{W}}})}$ measure as a function of the location of the third sensor, when the first two sensors (marked by the ![]() $\times$ and circle symbols) are fixed, for four different disturbance arrival angles: (a)
$\times$ and circle symbols) are fixed, for four different disturbance arrival angles: (a) ![]() $\theta = -90^\circ$, (b)
$\theta = -90^\circ$, (b) ![]() $\theta = -60^\circ$, (c)
$\theta = -60^\circ$, (c) ![]() $\theta = -20^\circ$ and (d)
$\theta = -20^\circ$ and (d) ![]() $\theta = 0^\circ$. The disturbance velocity vector is represented by the green arrow and the baseline vector between the first two sensors is denoted by the blue arrow.
$\theta = 0^\circ$. The disturbance velocity vector is represented by the green arrow and the baseline vector between the first two sensors is denoted by the blue arrow.
4. Numerical study
To study the performance of the DUET method and demonstrate computationally our method of estimating disturbance propagation velocity, we utilize LST to model the evolution of source mixtures in a BBL. We further use LST predictions as guidelines for designing the experimental set-up and determining the operational conditions of the experiments.
4.1. Generating disturbance source model via LST
We consider incompressible wall-bounded parallel shear flow with streamwise direction (![]() $x$), wall-normal direction (
$x$), wall-normal direction (![]() $y$) and spanwise direction (
$y$) and spanwise direction (![]() $z$). We decompose the total velocity field into a base flow of the form
$z$). We decompose the total velocity field into a base flow of the form ![]() $ {\boldsymbol {U}}= [U(y) \ \ 0 \ \ 0]^\textrm {T}$ and perturbed (
$ {\boldsymbol {U}}= [U(y) \ \ 0 \ \ 0]^\textrm {T}$ and perturbed (![]() $ {\boldsymbol {u}}^{(1)}$,
$ {\boldsymbol {u}}^{(1)}$, ![]() $p^{(1)}$) states about the base flow. All quantities are non-dimensionalized by the free-stream velocity,
$p^{(1)}$) states about the base flow. All quantities are non-dimensionalized by the free-stream velocity, ![]() $U_\infty$, and the boundary layer displacement thickness,
$U_\infty$, and the boundary layer displacement thickness, ![]() $\delta _d$, at a given streamwise position. This renders the Reynolds number
$\delta _d$, at a given streamwise position. This renders the Reynolds number ![]() $Re=U_\infty \delta _d/\nu$ as the governing parameter, where
$Re=U_\infty \delta _d/\nu$ as the governing parameter, where ![]() $\nu$ is the kinematic viscosity of the flow. The linearized Navier–Stokes equations are obtained by subtracting the equations for the base state from those corresponding to the total state, and dropping the nonlinear terms.
$\nu$ is the kinematic viscosity of the flow. The linearized Navier–Stokes equations are obtained by subtracting the equations for the base state from those corresponding to the total state, and dropping the nonlinear terms.
We analyse the stability of the mean flow with respect to wavelike velocity and pressure perturbations, also known as normal modes, for which
where ![]() $q^{(1)}=[u^{(1)} \ \ v^{(1)} \ \ w^{(1)}\ \ p^{(1)}]^\textrm {T}$, and
$q^{(1)}=[u^{(1)} \ \ v^{(1)} \ \ w^{(1)}\ \ p^{(1)}]^\textrm {T}$, and ![]() $\hat {q}(y)=[ \hat {u}(y) \ \ \hat {v}(y) \ \ \hat {w}(y) \ \ \hat {p}(y)]^\textrm {T}$ is the corresponding complex eigenvector. We consider the spatial case in which
$\hat {q}(y)=[ \hat {u}(y) \ \ \hat {v}(y) \ \ \hat {w}(y) \ \ \hat {p}(y)]^\textrm {T}$ is the corresponding complex eigenvector. We consider the spatial case in which ![]() $\alpha$ is a complex eigenvalue;
$\alpha$ is a complex eigenvalue; ![]() $\alpha _r\triangleq \textrm {Re}(\alpha )$ and
$\alpha _r\triangleq \textrm {Re}(\alpha )$ and ![]() $\beta$ are the disturbance streamwise and spanwise wavenumbers, respectively;
$\beta$ are the disturbance streamwise and spanwise wavenumbers, respectively; ![]() $\alpha _{im}\triangleq \textrm {Im}(\alpha )$ is the disturbance streamwise decay/growth rate for positive and negative values, respectively; and
$\alpha _{im}\triangleq \textrm {Im}(\alpha )$ is the disturbance streamwise decay/growth rate for positive and negative values, respectively; and ![]() $\omega$ is the dimensionless disturbance frequency. Substituting (4.1) into the linearized Navier–Stokes equations (which is equivalent to taking the Fourier transform) results in the following dispersion relation:
$\omega$ is the dimensionless disturbance frequency. Substituting (4.1) into the linearized Navier–Stokes equations (which is equivalent to taking the Fourier transform) results in the following dispersion relation:
This constitutes an eigenvalue problem for the complex eigenvalue ![]() $\alpha$ and its corresponding eigenfunction
$\alpha$ and its corresponding eigenfunction ![]() $\hat {q}$, for the given spanwise wavenumber
$\hat {q}$, for the given spanwise wavenumber ![]() $\beta$, the real frequency
$\beta$, the real frequency ![]() $\omega$, the Reynolds number
$\omega$, the Reynolds number ![]() $Re$ and the base flow velocity profile
$Re$ and the base flow velocity profile ![]() $U(y)$.
$U(y)$.
Following the primitive variable formulation in Schmid & Henningson (Reference Schmid and Henningson2001, p. 290), the dispersion relation (4.2) for the spatial case translates to the following system of equations:
 \begin{equation} \begin{bmatrix} 0 & -D & -\textrm{i}\beta & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ C & T & \textrm{i} U \beta & 0 & -D/Re & -\textrm{i}\beta/Re \\ 0 & -Re C & 0 & {Re}D & Re U & 0 \\ 0 & 0 & -Re C & \textrm{i}\beta Re & 0 & Re U \end{bmatrix} \begin{bmatrix} {\hat{u}} \\ {\hat{v}} \\ {\hat{w}} \\ {\hat{p}} \\ {\hat{v}_x} \\ {\hat{w}_x} \\ \end{bmatrix}=\textrm{i}\alpha \begin{bmatrix} {\hat{u}} \\ {\hat{v}} \\ {\hat{w}} \\ {\hat{p}} \\ {\hat{v}_x} \\ {\hat{w}_x} \\ \end{bmatrix}, \end{equation}
\begin{equation} \begin{bmatrix} 0 & -D & -\textrm{i}\beta & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ C & T & \textrm{i} U \beta & 0 & -D/Re & -\textrm{i}\beta/Re \\ 0 & -Re C & 0 & {Re}D & Re U & 0 \\ 0 & 0 & -Re C & \textrm{i}\beta Re & 0 & Re U \end{bmatrix} \begin{bmatrix} {\hat{u}} \\ {\hat{v}} \\ {\hat{w}} \\ {\hat{p}} \\ {\hat{v}_x} \\ {\hat{w}_x} \\ \end{bmatrix}=\textrm{i}\alpha \begin{bmatrix} {\hat{u}} \\ {\hat{v}} \\ {\hat{w}} \\ {\hat{p}} \\ {\hat{v}_x} \\ {\hat{w}_x} \\ \end{bmatrix}, \end{equation}
with homogeneous boundary conditions. For example, in BBL, ![]() $\hat {u} = \hat {v} = \hat {w} = \hat {v}_x = \hat {w}_x = 0$ at
$\hat {u} = \hat {v} = \hat {w} = \hat {v}_x = \hat {w}_x = 0$ at ![]() $y=0$ and
$y=0$ and ![]() $y\to \infty$ (see figure 4). Here
$y\to \infty$ (see figure 4). Here ![]() $C$ and
$C$ and ![]() $T$ denote the linear operators
$T$ denote the linear operators ![]() $C \triangleq \textrm {i}\omega + (D^2 - \beta ^2 )/Re$ and
$C \triangleq \textrm {i}\omega + (D^2 - \beta ^2 )/Re$ and ![]() $T \triangleq U D -U_y$. Both subscript
$T \triangleq U D -U_y$. Both subscript ![]() $(\cdot )_y$ and operator
$(\cdot )_y$ and operator ![]() $D$ denote the first derivative with respect to
$D$ denote the first derivative with respect to ![]() $y$, whereas
$y$, whereas ![]() $(\cdot )_x$ denotes the first derivative with respect to
$(\cdot )_x$ denotes the first derivative with respect to ![]() $x$.
$x$.

Figure 4. Flow over a flat plate.
Thus, we have a boundary value problem for the above system, which we solve numerically with the aid of Matlab, utilizing spectral methods (Trefethen Reference Trefethen2000) with ![]() $150$ grid points. The results of the numerical dispersion relation solution are validated against reported results in the literature for the BBL (Jordinson Reference Jordinson1970; Schmid & Henningson Reference Schmid and Henningson2001; Boiko et al. Reference Boiko, Dovgal, Grek and Kozlov2011). We search for the most unstable TS wave, where its eigenmode is obtained from (4.3), and its amplitude profile is represented by the corresponding
$150$ grid points. The results of the numerical dispersion relation solution are validated against reported results in the literature for the BBL (Jordinson Reference Jordinson1970; Schmid & Henningson Reference Schmid and Henningson2001; Boiko et al. Reference Boiko, Dovgal, Grek and Kozlov2011). We search for the most unstable TS wave, where its eigenmode is obtained from (4.3), and its amplitude profile is represented by the corresponding ![]() $|\hat {q}(y)|$.
$|\hat {q}(y)|$.
In addition to TS waves we also consider WP sources. A single WP disturbance may be generated by a short pulse actuation of the boundary layer at a specific location. The short pulse generates a localized disturbance that may be regarded as a linear superposition of many TS waves associated with a wide range of frequencies that may grow or decay downstream in the boundary layer. We focus on the long-time instability characteristics of the WP, far away from the pulse actuation location, after the WP transient behaviour has decayed. Each of the WP modes travels with its own phase velocity, given by
but all modes share the same group velocity:
In (4.5), ![]() $\nabla _k=[{\partial }/{\partial \alpha }\ \ {\partial }/{\partial \beta }]^\textrm {T}$ and
$\nabla _k=[{\partial }/{\partial \alpha }\ \ {\partial }/{\partial \beta }]^\textrm {T}$ and ![]() $ {\boldsymbol {k}}$ is a real wavenumber vector, defined as
$ {\boldsymbol {k}}$ is a real wavenumber vector, defined as
i.e. ![]() $c_x=\textrm {Re}\{\alpha \}\omega /| {\boldsymbol {k}}|^2$ and
$c_x=\textrm {Re}\{\alpha \}\omega /| {\boldsymbol {k}}|^2$ and ![]() $c_z=\beta \omega /| {\boldsymbol {k}}|^2$.
$c_z=\beta \omega /| {\boldsymbol {k}}|^2$.
Following the theoretical model proposed in Gaster (Reference Gaster1975), the model for a single three-dimensional WP source in non-parallel shear flow is given by
 \begin{align} &u_{WP}(x,y_0,z,t) \nonumber\\ &\quad = A(y_0)\ \textrm{Re}\left\{ x^{ - 1/4}\sum_{{\omega _n} = {\omega _0}}^{{\omega _N}}\sum_{{\beta _k} = {\beta _0}}^{{\beta _M}} {\exp{ {\textrm{i}\left[ {\int_{{x_0}}^x {\alpha ( {\zeta, \beta _k,{\omega _n}} )} \,\textrm{d}\zeta+\beta_k (z-z_0) - \omega_n t} \right]}}} \right\}, \end{align}
\begin{align} &u_{WP}(x,y_0,z,t) \nonumber\\ &\quad = A(y_0)\ \textrm{Re}\left\{ x^{ - 1/4}\sum_{{\omega _n} = {\omega _0}}^{{\omega _N}}\sum_{{\beta _k} = {\beta _0}}^{{\beta _M}} {\exp{ {\textrm{i}\left[ {\int_{{x_0}}^x {\alpha ( {\zeta, \beta _k,{\omega _n}} )} \,\textrm{d}\zeta+\beta_k (z-z_0) - \omega_n t} \right]}}} \right\}, \end{align}
where ![]() $u_{WP}(x,y_0,z,t)$ is the streamwise velocity of the WP at a given wall-normal height
$u_{WP}(x,y_0,z,t)$ is the streamwise velocity of the WP at a given wall-normal height ![]() $y_0$,
$y_0$, ![]() $(x_0, z_0)$ is the location where the WP source is generated and
$(x_0, z_0)$ is the location where the WP source is generated and ![]() $(x, z)$ is the location where the WP source is measured. In our case of flow over a flat plate, the origin of the
$(x, z)$ is the location where the WP source is measured. In our case of flow over a flat plate, the origin of the ![]() $x$ axis is at the plate's leading edge. The term
$x$ axis is at the plate's leading edge. The term ![]() $x^{-1/4}$ has been included to compensate for the slight divergence of the mean flow (a model that accounts for downstream eigenfunction variation is provided in Cohen (Reference Cohen1994)). Under the parallel flow assumption, we obtain
$x^{-1/4}$ has been included to compensate for the slight divergence of the mean flow (a model that accounts for downstream eigenfunction variation is provided in Cohen (Reference Cohen1994)). Under the parallel flow assumption, we obtain
 \begin{align} u_{WP}(x,y_0,z,t) =A(y_0)\ \textrm{Re}\left\{ \sum_{{\omega _n} = {\omega _0}}^{{\omega _N}}\sum_{{\beta _k} = {\beta _0}}^{{\beta _M}} {\exp \{ {\textrm{i}[ {\alpha_{x_0,\omega_n,\beta_k}(x - x_0) + \beta_k (z-z_0) - \omega_n t} ]} \}} \right\}. \end{align}
\begin{align} u_{WP}(x,y_0,z,t) =A(y_0)\ \textrm{Re}\left\{ \sum_{{\omega _n} = {\omega _0}}^{{\omega _N}}\sum_{{\beta _k} = {\beta _0}}^{{\beta _M}} {\exp \{ {\textrm{i}[ {\alpha_{x_0,\omega_n,\beta_k}(x - x_0) + \beta_k (z-z_0) - \omega_n t} ]} \}} \right\}. \end{align}
Here, the eigenvalue ![]() $\alpha _{x_0}$ associated with
$\alpha _{x_0}$ associated with ![]() $\omega _n,\beta _k$ is kept constant along the streamwise direction. The model presented in (4.8) is a simplified version of the theoretical model proposed in Gaster (Reference Gaster1975) and Cohen (Reference Cohen1994). Its simplicity notwithstanding, this model provides estimates of the development of a WP disturbance over the relatively short distances between the sensors that are adequate for testing the performance of our DUET-based method prior to proceeding to experimental studies.
$\omega _n,\beta _k$ is kept constant along the streamwise direction. The model presented in (4.8) is a simplified version of the theoretical model proposed in Gaster (Reference Gaster1975) and Cohen (Reference Cohen1994). Its simplicity notwithstanding, this model provides estimates of the development of a WP disturbance over the relatively short distances between the sensors that are adequate for testing the performance of our DUET-based method prior to proceeding to experimental studies.
4.2. Using LST to model sensor measurement
We implement the LST model under the parallel flow assumption for generating simulated mixtures of ![]() $N_s$ disturbance sources that are measured by
$N_s$ disturbance sources that are measured by ![]() $N_x$ sensors. The disturbances considered comprise TS wave sources and WP sources. In the case of a single TS wave disturbance measured at a specific wall-normal height
$N_x$ sensors. The disturbances considered comprise TS wave sources and WP sources. In the case of a single TS wave disturbance measured at a specific wall-normal height ![]() $y_0$, (4.1) can be written as
$y_0$, (4.1) can be written as
In (4.9) the phase shift in time, ![]() $\phi _t$, at
$\phi _t$, at ![]() $y_0$ is determined by the spatial parameters of the disturbance
$y_0$ is determined by the spatial parameters of the disturbance
where ![]() $\phi _{t_0}$ is the initial phase and
$\phi _{t_0}$ is the initial phase and ![]() $(x,z)$ are the current location coordinates.
$(x,z)$ are the current location coordinates.
A source is defined as the signal that would have been measured by a sensor if all other sources were nil (that is, when no other mechanically generated signal is sensed). Each source is generated by a particular physical disturbance generator, which characterizes its signature in the sensor recordings. The source ![]() $s_j$ is defined by its frequency
$s_j$ is defined by its frequency ![]() $\omega _j$ and the initial phase
$\omega _j$ and the initial phase ![]() $\phi _{t_{0_j}}$ it had at its introduction location
$\phi _{t_{0_j}}$ it had at its introduction location ![]() ${ {\boldsymbol {r}}}_{s_j} = [l_x \ \ l_z]_{s_j}$ on the
${ {\boldsymbol {r}}}_{s_j} = [l_x \ \ l_z]_{s_j}$ on the ![]() $x$–
$x$–![]() $z$ plane. Let
$z$ plane. Let ![]() ${ {\boldsymbol {r}}}_{x_i} = [l_x \ \ l_z]_{x_i}^\textrm {T}$ be the location of sensor
${ {\boldsymbol {r}}}_{x_i} = [l_x \ \ l_z]_{x_i}^\textrm {T}$ be the location of sensor ![]() $i$ on the
$i$ on the ![]() $x$–
$x$–![]() $z$ plane, where
$z$ plane, where ![]() $x_i$ stands for the signal measured by that sensor.
$x_i$ stands for the signal measured by that sensor.
Using (4.9) and (4.10), we represent the measurement of source ![]() $s_j$ by sensor
$s_j$ by sensor ![]() $i$ as
$i$ as
where ![]() $\phi _{t_{ij}}$, the phase of source
$\phi _{t_{ij}}$, the phase of source ![]() $s_j$ as measured by sensor
$s_j$ as measured by sensor ![]() $i$, is given by
$i$, is given by
In (4.12), ![]() $[l_x]_{x_i}-[l_x]_{s_j}$ and
$[l_x]_{x_i}-[l_x]_{s_j}$ and ![]() $[l_z]_{x_i}-[l_z]_{s_j}$ are the downstream and spanwise distances, respectively, that the disturbance
$[l_z]_{x_i}-[l_z]_{s_j}$ are the downstream and spanwise distances, respectively, that the disturbance ![]() $s_j$ travels from its generation point to sensor
$s_j$ travels from its generation point to sensor ![]() $i$. The variation in the phase of source
$i$. The variation in the phase of source ![]() $s_j$ at the recording location of sensor
$s_j$ at the recording location of sensor ![]() $i$ is due to the spatial wavenumbers
$i$ is due to the spatial wavenumbers ![]() $\alpha _{r_j}$,
$\alpha _{r_j}$, ![]() $\beta _j$, and the eigenvector phase
$\beta _j$, and the eigenvector phase ![]() $\phi _j(y)$ of the source
$\phi _j(y)$ of the source ![]() $s_j$ at the vertical location
$s_j$ at the vertical location ![]() $[l_y]_{x_i}$ of sensor
$[l_y]_{x_i}$ of sensor ![]() $i$.
$i$.
Similarly, for a WP source generated at ![]() ${ {\boldsymbol {r}}}_{s_j}$ and measured by sensor
${ {\boldsymbol {r}}}_{s_j}$ and measured by sensor ![]() $i$, we have
$i$, we have
 \begin{align} s_{ij}= \textrm{Re}\left\{ \sum_{\omega _n = \omega _0}^{\omega _N}\sum_{\beta _k = \beta _0}^{\beta _M} \exp \{ \textrm{i}[ \alpha_{ x_{s_j},\omega _n,\beta _k } ( [l_x]_{x_i} - [l_x]_{s_j} ) + \beta_k ([l_z]_{x_i} - [l_z]_{s_j}) - \omega_n t ] \} \right\}. \end{align}
\begin{align} s_{ij}= \textrm{Re}\left\{ \sum_{\omega _n = \omega _0}^{\omega _N}\sum_{\beta _k = \beta _0}^{\beta _M} \exp \{ \textrm{i}[ \alpha_{ x_{s_j},\omega _n,\beta _k } ( [l_x]_{x_i} - [l_x]_{s_j} ) + \beta_k ([l_z]_{x_i} - [l_z]_{s_j}) - \omega_n t ] \} \right\}. \end{align}
Finally, the source mixture measured by sensor ![]() $i$ in the presence of
$i$ in the presence of ![]() $N_s$ sources is
$N_s$ sources is
 \begin{equation} x_i = \sum_{j = 1}^{N_s} s_{ij},\quad i = 1,2,\ldots N_x. \end{equation}
\begin{equation} x_i = \sum_{j = 1}^{N_s} s_{ij},\quad i = 1,2,\ldots N_x. \end{equation}
Equation (4.14) provides a general model for a system consisting of ![]() $N_x$ sensors measuring
$N_x$ sensors measuring ![]() $N_s$ TS and WP disturbance sources, represented by (4.11) and (4.13), respectively.
$N_s$ TS and WP disturbance sources, represented by (4.11) and (4.13), respectively.
4.3. Numerical settings and procedure
The dispersion relation is solved for ![]() $\alpha$ and
$\alpha$ and ![]() $q$ for the given frequency
$q$ for the given frequency ![]() $\omega$, spanwise wavenumber
$\omega$, spanwise wavenumber ![]() $\beta$, Reynolds number
$\beta$, Reynolds number ![]() $Re$ and base flow velocity profile
$Re$ and base flow velocity profile ![]() $U(y)$ of BBL under the quasi-parallel flow assumption. We consider air flow at room temperature with kinematic viscosity
$U(y)$ of BBL under the quasi-parallel flow assumption. We consider air flow at room temperature with kinematic viscosity ![]() $\nu = 0.15\times 10^{-4}$ m
$\nu = 0.15\times 10^{-4}$ m![]() $^2$ s
$^2$ s![]() $^{-1}$, and the free-stream velocity is set to
$^{-1}$, and the free-stream velocity is set to ![]() $U_{\infty }=5$ m s
$U_{\infty }=5$ m s![]() $^{-1}$. The disturbance sources are introduced at various downstream locations (
$^{-1}$. The disturbance sources are introduced at various downstream locations (![]() $ {\boldsymbol {r}}_{s_j}$) with various frequencies. Each given pair of frequency and downstream injection location of each source is associated with the corresponding non-dimensional frequency
$ {\boldsymbol {r}}_{s_j}$) with various frequencies. Each given pair of frequency and downstream injection location of each source is associated with the corresponding non-dimensional frequency ![]() $\omega$ and the local Reynolds number, which is based on the local displacement thickness, i.e.
$\omega$ and the local Reynolds number, which is based on the local displacement thickness, i.e. ![]() $Re(x)= U_\infty \delta _d(x)/\nu$ (for BBL the displacement thickness is given by
$Re(x)= U_\infty \delta _d(x)/\nu$ (for BBL the displacement thickness is given by ![]() $\delta _d(x) = 1.7208 \sqrt {\nu x/U_\infty }$). These are used to solve the dispersion relation for the spatial case. The sensors are set to measure the streamwise component of the flow,
$\delta _d(x) = 1.7208 \sqrt {\nu x/U_\infty }$). These are used to solve the dispersion relation for the spatial case. The sensors are set to measure the streamwise component of the flow, ![]() $u$. The obtained eigenvalues
$u$. The obtained eigenvalues ![]() $\alpha$ and eigenfunctions
$\alpha$ and eigenfunctions ![]() $\hat u$ are used as inputs to the truth model, which consists of simulated source mixtures, measured by the sensors in the LST model. The simulations are performed in dimensional form, where the dimensionless parameters
$\hat u$ are used as inputs to the truth model, which consists of simulated source mixtures, measured by the sensors in the LST model. The simulations are performed in dimensional form, where the dimensionless parameters ![]() $\omega$ and
$\omega$ and ![]() $\alpha$ of each source are dimensionalized using the local displacement thickness at the injection location of the source and
$\alpha$ of each source are dimensionalized using the local displacement thickness at the injection location of the source and ![]() $U_{\infty }$. For simplicity and clarity of exposition, the non-parallel effect is neglected in our truth model, where it is assumed that the source eigenvalues and eigenfunctions remain unchanged during their downstream propagation towards the sensors. In reality, the non-parallel effect may significantly modify the amplitudes and phases of the sources at the location of the sensor, if the sources travel a long distance (many wavelengths) from their respective injection locations to the sensor. Nevertheless, the downstream distance between two neighbouring sensors, a key variable in the DUET method, is extremely small, compared with the disturbance wavelength. Therefore, the non-parallel effect is deemed negligible in our study, which is aimed at demonstrating the viability of the DUET method.
$U_{\infty }$. For simplicity and clarity of exposition, the non-parallel effect is neglected in our truth model, where it is assumed that the source eigenvalues and eigenfunctions remain unchanged during their downstream propagation towards the sensors. In reality, the non-parallel effect may significantly modify the amplitudes and phases of the sources at the location of the sensor, if the sources travel a long distance (many wavelengths) from their respective injection locations to the sensor. Nevertheless, the downstream distance between two neighbouring sensors, a key variable in the DUET method, is extremely small, compared with the disturbance wavelength. Therefore, the non-parallel effect is deemed negligible in our study, which is aimed at demonstrating the viability of the DUET method.
4.4. The DUET settings
The signals are acquired at a 1 kHz sample rate. In order to apply DUET to the two measured mixtures, we set the initial values of the DUET parameters for flow measurements according to those recommended for speech mixtures by Rickard (Reference Rickard2007).
(i) Window size. The window size of the short Fourier transform is set to 256 ms. The window size is important for good DUET performance and description of the frequencies in the flow. Increasing the window size will result in good frequency localization in the time–frequency domain, but the time localization will deteriorate. Too narrow a window size will result in a poor frequency resolution, but will increase the time resolution. In Rickard (Reference Rickard2007), it was found that speech is most window-disjoint orthogonal when a window of 1024 samples is used, corresponding to a length of 64 ms. In our study of shear flows, we found that good window sizes appropriate for time scales in our measurements are of 128–512 ms in length, corresponding to 128–512 samples at 1 kHz sample rate. This range results in a trade-off between frequency and time resolution (128 samples in favour of time resolution and 512 samples in favour of frequency resolution).
(ii) Histogram domain. The histogram domain
 $I(\alpha ,\delta )$ is divided into 105 bins by 150 bins. The smoothing resolutions (
$I(\alpha ,\delta )$ is divided into 105 bins by 150 bins. The smoothing resolutions ( $\varDelta _\alpha$ and
$\varDelta _\alpha$ and  $\varDelta _\delta$) are set such that the weighted clusters of peaks that emerge on the histogram domain, centred on the actual mixing parameter pairs, are smoothed with a 3-by-3 neighbouring-bins window. This facilitates determination of localized histogram peaks.
$\varDelta _\delta$) are set such that the weighted clusters of peaks that emerge on the histogram domain, centred on the actual mixing parameter pairs, are smoothed with a 3-by-3 neighbouring-bins window. This facilitates determination of localized histogram peaks.(iii) Histogram weights. Motivated by the maximum-likelihood symmetric attenuation estimator in Yilmaz & Rickard (Reference Yilmaz and Rickard2004), we set
 $p=1$ and
$p=1$ and  $q=0$. Good DUET performance is also obtained by setting
$q=0$. Good DUET performance is also obtained by setting  $p=2$ and
$p=2$ and  $q=0$, to reduce delay estimator bias (Yilmaz & Rickard Reference Yilmaz and Rickard2004).
$q=0$, to reduce delay estimator bias (Yilmaz & Rickard Reference Yilmaz and Rickard2004).
Next, two numerical examples are presented to study DUET performance when using various sensor configurations in various source mixing scenarios. The first example, which addresses five two-dimensional sources with two sensors placed at different heights, tests DUET as a source separation method. The second example, which addresses three three-dimensional sources with different propagation directions, sampled by a configuration of three sensors sharing the same height, tests the method's performance on each separated source.
4.5. Example 1: disturbance mixture separation
This example serves to test and demonstrate the capabilities of DUET as a source identification and separation method in boundary layer measurement applications. To this end, our truth model comprises a five-source mixture, introduced upstream of the sensors. In particular, ![]() $s_1$ and
$s_1$ and ![]() $s_4$ are two-dimensional WPs introduced at downstream locations
$s_4$ are two-dimensional WPs introduced at downstream locations ![]() $x=0.36$ m and
$x=0.36$ m and ![]() $x=1.0$ m (recall that the origin,
$x=1.0$ m (recall that the origin, ![]() $x=0$, is located at the plate's leading edge). These locations correspond to Reynolds numbers
$x=0$, is located at the plate's leading edge). These locations correspond to Reynolds numbers ![]() $Re_1=600$ and
$Re_1=600$ and ![]() $Re_4=1000$, respectively. The sources
$Re_4=1000$, respectively. The sources ![]() $s_2$,
$s_2$, ![]() $s_3$ and
$s_3$ and ![]() $s_5$ are two-dimensional TS waves, introduced at downstream locations
$s_5$ are two-dimensional TS waves, introduced at downstream locations ![]() $x=0.25$ m,
$x=0.25$ m, ![]() $x=2$ m and
$x=2$ m and ![]() $x=0.57$ m, corresponding to
$x=0.57$ m, corresponding to ![]() $Re_2=500$,
$Re_2=500$, ![]() $Re_3=1400$ and
$Re_3=1400$ and ![]() $Re_5=750$, respectively. The TS source dimensionless frequencies are
$Re_5=750$, respectively. The TS source dimensionless frequencies are ![]() $\omega _2=0.12$,
$\omega _2=0.12$, ![]() $\omega _3=0.04$ and
$\omega _3=0.04$ and ![]() $\omega _5=0.07$, corresponding to 63.7, 7.6 and 24.8 Hz, respectively. The stability properties of the sources are illustrated in figure 5.
$\omega _5=0.07$, corresponding to 63.7, 7.6 and 24.8 Hz, respectively. The stability properties of the sources are illustrated in figure 5.

Figure 5. Truth-model sources. WP sources ![]() $s_1$ (magenta dashed line) and
$s_1$ (magenta dashed line) and ![]() $s_4$ (cyan dashed line) at specific
$s_4$ (cyan dashed line) at specific ![]() $Re$; TS source eigenvalues, denoted by asterisk symbols:
$Re$; TS source eigenvalues, denoted by asterisk symbols: ![]() $\alpha _{s_2} =0.3014 + 0.0006\textrm {i}$ (red),
$\alpha _{s_2} =0.3014 + 0.0006\textrm {i}$ (red), ![]() $\alpha _{s_3} =0.1347 + 0.0009\textrm {i}$ (green) and
$\alpha _{s_3} =0.1347 + 0.0009\textrm {i}$ (green) and ![]() $\alpha _{s_5} =0.2010 + 0.0002\textrm {i}$ (blue) at specific (
$\alpha _{s_5} =0.2010 + 0.0002\textrm {i}$ (blue) at specific (![]() $Re$,
$Re$, ![]() $\omega$). Sources plotted over contours of constant streamwise wavenumber
$\omega$). Sources plotted over contours of constant streamwise wavenumber ![]() $\alpha _r$ (dotted black contours), growth rate
$\alpha _r$ (dotted black contours), growth rate ![]() $\alpha _{im}$ (solid black contours). The neutral curve is denoted by the bold black contour.
$\alpha _{im}$ (solid black contours). The neutral curve is denoted by the bold black contour.
The sensors are located at ![]() $[l_x]_{x_1} = 2.29$ m and
$[l_x]_{x_1} = 2.29$ m and ![]() $[l_x]_{x_2} = [l_x]_{x_1} + 0.005$ m. The downstream separation of 0.005 m between the sensors is chosen to satisfy the fourth underlying assumption of the DUET method. Accordingly, figure 5 shows that the slowest TS disturbances propagate at a velocity of approximately
$[l_x]_{x_2} = [l_x]_{x_1} + 0.005$ m. The downstream separation of 0.005 m between the sensors is chosen to satisfy the fourth underlying assumption of the DUET method. Accordingly, figure 5 shows that the slowest TS disturbances propagate at a velocity of approximately ![]() $(c_r)_{max}\approx 0.3U_\infty$, and the maximal frequency in the simulated mixture (see figure 7), associated with TS source
$(c_r)_{max}\approx 0.3U_\infty$, and the maximal frequency in the simulated mixture (see figure 7), associated with TS source ![]() $s_2$, is
$s_2$, is ![]() $\,f_m=\,f_{2} = 63$ Hz. Using (2.6) yields
$\,f_m=\,f_{2} = 63$ Hz. Using (2.6) yields ![]() $|[l_x]_{x_1} - [l_x]_{x_2}| < {{\rm \pi} c_r}/{\omega _m}={0.3U_\infty }/{2f_m}\approx 0.0118$ m, rendering an upper bound on the limiting distance between the sensors. We place each sensor at a different height above the plate: sensor 1 at 2 mm and sensor 2 at 1.4 mm. The simulated TS eigenfunction profiles (amplitude and phase of the streamwise disturbance velocity) are shown in figure 6, where the sensor positions are indicated by the horizontal lines (near the inner maximum of the streamwise component of the TS disturbance profiles).
$|[l_x]_{x_1} - [l_x]_{x_2}| < {{\rm \pi} c_r}/{\omega _m}={0.3U_\infty }/{2f_m}\approx 0.0118$ m, rendering an upper bound on the limiting distance between the sensors. We place each sensor at a different height above the plate: sensor 1 at 2 mm and sensor 2 at 1.4 mm. The simulated TS eigenfunction profiles (amplitude and phase of the streamwise disturbance velocity) are shown in figure 6, where the sensor positions are indicated by the horizontal lines (near the inner maximum of the streamwise component of the TS disturbance profiles).

Figure 6. Streamwise component (![]() $u$) of the three TS sources:
$u$) of the three TS sources: ![]() $s_2$ (red),
$s_2$ (red), ![]() $s_3$ (green) and
$s_3$ (green) and ![]() $s_5$ (blue). (a) Eigenfunction amplitude (normalized by its maximum) and (b) eigenfunction phase. Black lines: height of sensor 1 (solid) and sensor 2 (dashed). The sensor heights are related to the correct positions at the eigenfunction profiles of the sources by rescaling the
$s_5$ (blue). (a) Eigenfunction amplitude (normalized by its maximum) and (b) eigenfunction phase. Black lines: height of sensor 1 (solid) and sensor 2 (dashed). The sensor heights are related to the correct positions at the eigenfunction profiles of the sources by rescaling the ![]() $y$ axis with the average
$y$ axis with the average ![]() $\delta _d$ of all injection locations of the TS sources.
$\delta _d$ of all injection locations of the TS sources.
Figures 7(a) and 7(d) display the outputs of two sensors that are used to measure the streamwise velocity component over a 2 s time interval. The corresponding Fourier transforms are shown in figures 7(b) and 7(e), and the spectrograms of the mixtures are shown in figures 7(c) and 7(f), respectively. Examination of figures 7(b) and 7(e) reveals that each measured mixture contains the frequencies of the introduced sources. Each TS source has a unique single frequency, whereas the WP typical spectrum looks like a bell-shaped signature centred about a dominant frequency of around 50 Hz for ![]() $s_1$ and 24 Hz for
$s_1$ and 24 Hz for ![]() $s_4$. Figures 7(c) and 7(f) demonstrate that the second DUET assumption (WDO) is not fully satisfied. Specifically, the WP source
$s_4$. Figures 7(c) and 7(f) demonstrate that the second DUET assumption (WDO) is not fully satisfied. Specifically, the WP source ![]() $s_1$ and the TS source
$s_1$ and the TS source ![]() $s_2$ co-dominate the flow for a certain time–frequency range. Similarly, but to a lesser degree, the WP source
$s_2$ co-dominate the flow for a certain time–frequency range. Similarly, but to a lesser degree, the WP source ![]() $s_4$ and the TS source
$s_4$ and the TS source ![]() $s_5$ coexist for a certain time–frequency range.
$s_5$ coexist for a certain time–frequency range.

Figure 7. True (LST-computed) mixtures as measured by two sensors: (a) ![]() $x_1$ and (d)
$x_1$ and (d) ![]() $x_2$. Corresponding Fourier transforms: (b)
$x_2$. Corresponding Fourier transforms: (b) ![]() $E_{x_1}$ and (e)
$E_{x_1}$ and (e) ![]() $E_{x_2}$. Absolute values of windowed Fourier transforms (spectrograms), for which a window of 256 samples is used: (c)
$E_{x_2}$. Absolute values of windowed Fourier transforms (spectrograms), for which a window of 256 samples is used: (c) ![]() $20\log (|\hat {x}_1|+10^{-6})$ dB and (f)
$20\log (|\hat {x}_1|+10^{-6})$ dB and (f) ![]() $20\log (|\hat {x}_2|+10^{-6})$ dB.
$20\log (|\hat {x}_2|+10^{-6})$ dB.
Figure 8 shows that the DUET-based method successfully identifies the correct number of sources. The isometric view of the histogram, presented in figure 8(b), shows five peaks associated with five true sources. Three peaks are related to the three TS sources and the other two peaks are associated with the WP sources. Figure 8(a) displays the mixing-parameter pairs of the true (LST-computed) TS sources, together with the peak contours. Clearly, three of the histogram peaks coincide with the mixing parameters of the true TS sources, ![]() $s_2$,
$s_2$, ![]() $s_3$ and
$s_3$ and ![]() $s_5$. The other two peaks are associated with the WP sources,
$s_5$. The other two peaks are associated with the WP sources, ![]() $s_1$ and
$s_1$ and ![]() $s_4$. In this example, histogram peaks are clustered around similar values of
$s_4$. In this example, histogram peaks are clustered around similar values of ![]() $\delta$. The height difference between sensors has a strong effect on the
$\delta$. The height difference between sensors has a strong effect on the ![]() $\alpha$ parameter. Thus, placing the sensors at different heights increases the scatter along the
$\alpha$ parameter. Thus, placing the sensors at different heights increases the scatter along the ![]() $\alpha$ axis, which facilitates distinguishing between the histogram peaks.
$\alpha$ axis, which facilitates distinguishing between the histogram peaks.

Figure 8. A DUET two-dimensional cross power weighted ![]() $(p = 1, q = 0)$ histogram of symmetric attenuation
$(p = 1, q = 0)$ histogram of symmetric attenuation ![]() $\alpha =(a - 1/a)$ and delay estimate pairs from two mixtures of five sources. (a) Contour plot (black) of the two-dimensional histogram with corresponding true (LST-computed) mixing parameter pairs for each TS source:
$\alpha =(a - 1/a)$ and delay estimate pairs from two mixtures of five sources. (a) Contour plot (black) of the two-dimensional histogram with corresponding true (LST-computed) mixing parameter pairs for each TS source: ![]() $s_2$ (red),
$s_2$ (red), ![]() $s_3$ (green) and
$s_3$ (green) and ![]() $s_5$ (blue). (b) Isometric view.
$s_5$ (blue). (b) Isometric view.
Obtained from the histogram peak locations, the identified mixing parameters are used to demix the sources. Figure 9 shows five estimated sources, denoted by ![]() $y_j$,
$y_j$, ![]() $j=1,2,3,4,5$, as identified by the DUET method. Figures 9(a) and 9(j) depict the time signatures of the estimates of sources
$j=1,2,3,4,5$, as identified by the DUET method. Figures 9(a) and 9(j) depict the time signatures of the estimates of sources ![]() $s_1$ and
$s_1$ and ![]() $s_4$, clearly featuring typical WP structures. Nonetheless, figure 9(l) shows that the estimate of WP source
$s_4$, clearly featuring typical WP structures. Nonetheless, figure 9(l) shows that the estimate of WP source ![]() $s_4$ contains a weak spurious signal at 50 Hz. This frequency is also shared by TS source
$s_4$ contains a weak spurious signal at 50 Hz. This frequency is also shared by TS source ![]() $s_5$. Figure 9(m–o) shows that the spectrum of the estimate of TS source
$s_5$. Figure 9(m–o) shows that the spectrum of the estimate of TS source ![]() $s_5$ is not contaminated by the estimates of other sources. However, it is attenuated in the region where WP source
$s_5$ is not contaminated by the estimates of other sources. However, it is attenuated in the region where WP source ![]() $s_4$ is active. Figure 9(g–i) indicates that the estimate of TS source
$s_4$ is active. Figure 9(g–i) indicates that the estimate of TS source ![]() $s_3$ contains very weak signatures (50 dB) of
$s_3$ contains very weak signatures (50 dB) of ![]() $s_4$, which do not affect its time signature. In this example we verified that multiple WP and TS disturbance sources in shear flows (sufficiently) satisfy the WDO condition, thus allowing accurate mixing parameter estimation with only two sensors, which yields high-fidelity signal recovery using DUET.
$s_4$, which do not affect its time signature. In this example we verified that multiple WP and TS disturbance sources in shear flows (sufficiently) satisfy the WDO condition, thus allowing accurate mixing parameter estimation with only two sensors, which yields high-fidelity signal recovery using DUET.

Figure 9. The DUET estimates of sources: (a) ![]() $y_1$, (d)
$y_1$, (d) ![]() $y_2$, (g)
$y_2$, (g) ![]() $y_3$, (j)
$y_3$, (j) ![]() $y_4$ and (m)
$y_4$ and (m) ![]() $y_5$. Corresponding Fourier transforms: (b)
$y_5$. Corresponding Fourier transforms: (b) ![]() $E_{y_1}$, (e)
$E_{y_1}$, (e) ![]() $E_{y_2}$, (h)
$E_{y_2}$, (h) ![]() $E_{y_3}$, (k)
$E_{y_3}$, (k) ![]() $E_{y_4}$ and (n)
$E_{y_4}$ and (n) ![]() $E_{y_5}$. Corresponding spectrograms (dB): (c)
$E_{y_5}$. Corresponding spectrograms (dB): (c) ![]() $|\hat {y}_1|$, (f)
$|\hat {y}_1|$, (f) ![]() $|\hat {y}_2|$, (i)
$|\hat {y}_2|$, (i) ![]() $|\hat {y}_3|$, (l)
$|\hat {y}_3|$, (l) ![]() $|\hat {y}_4|$ and (o)
$|\hat {y}_4|$ and (o) ![]() $|\hat {y}_5|$.
$|\hat {y}_5|$.
4.6. Example 2: disturbance velocity estimation
This example is used to demonstrate how our DUET-based method can be used to estimate the propagation velocity of disturbances in the flow using only three sensors, appropriately placed in the flow field. As in the previous example, LST is used for generating a truth model comprising a mixture of three sources: two three-dimensional TS (oblique) waves and one two-dimensional WP source. The three disturbance sources are introduced at different locations upstream of the sensors, as detailed in table 1, which also lists the source parameters.
Table 1. Disturbance sources.

The frequencies of the TS sources ![]() $s_2$ and
$s_2$ and ![]() $s_3$ are 53.1 and 22.7 Hz, respectively. Their corresponding eigenvalues are obtained by solving the dispersion relation for the spatial case, which results in
$s_3$ are 53.1 and 22.7 Hz, respectively. Their corresponding eigenvalues are obtained by solving the dispersion relation for the spatial case, which results in ![]() $\alpha _2 = 0.2987 + 0.0003\textrm {i}$ and
$\alpha _2 = 0.2987 + 0.0003\textrm {i}$ and ![]() $\alpha _3= 0.1613 + 0.0039\textrm {i}$. The propagation angle of a TS source is given by
$\alpha _3= 0.1613 + 0.0039\textrm {i}$. The propagation angle of a TS source is given by
which yields ![]() $26.7^\circ$ for
$26.7^\circ$ for ![]() $s_2$ and
$s_2$ and ![]() $-42.9^\circ$ for
$-42.9^\circ$ for ![]() $s_3$. The angle of the two-dimensional WP (
$s_3$. The angle of the two-dimensional WP (![]() $\beta =0$) source
$\beta =0$) source ![]() $s_1$ is
$s_1$ is ![]() $0^\circ$. The propagation velocities of the TS sources correspond to their phase velocities as given by (4.4) from which we obtain that the TS waves travel at speeds
$0^\circ$. The propagation velocities of the TS sources correspond to their phase velocities as given by (4.4) from which we obtain that the TS waves travel at speeds ![]() $c_2= 1.7950$ m s
$c_2= 1.7950$ m s![]() $^{-1}$ and
$^{-1}$ and ![]() $c_3= 1.3618$ m s
$c_3= 1.3618$ m s![]() $^{-1}$ along their respective wave vector directions. In the case of the WP source, each of its many modes propagates with its own phase velocity, which differs from those of the other modes, but all travel as a group of waves at a group velocity
$^{-1}$ along their respective wave vector directions. In the case of the WP source, each of its many modes propagates with its own phase velocity, which differs from those of the other modes, but all travel as a group of waves at a group velocity ![]() $ {\boldsymbol {c}}_g$, also known as the WP envelope velocity. This velocity can be obtained by monitoring the leading edge and the trailing edge of the WP envelope in the
$ {\boldsymbol {c}}_g$, also known as the WP envelope velocity. This velocity can be obtained by monitoring the leading edge and the trailing edge of the WP envelope in the ![]() $t$–
$t$–![]() $x$ domain (Gaster Reference Gaster1975). For
$x$ domain (Gaster Reference Gaster1975). For ![]() $Re=851$ it is shown in Gaster & Grant (Reference Gaster and Grant1975) that the leading edge of a three-dimensional WP propagates at 0.44 of the free-stream value, whereas the trailing edge seems to exhibit some local transient behaviour near the source before settling down to a path with a slope of 0.36
$Re=851$ it is shown in Gaster & Grant (Reference Gaster and Grant1975) that the leading edge of a three-dimensional WP propagates at 0.44 of the free-stream value, whereas the trailing edge seems to exhibit some local transient behaviour near the source before settling down to a path with a slope of 0.36![]() $U_{\infty }$. In particular, figure 10 shows the velocity of the WP in our simulation. In this figure we denote the time when the maximum value of the envelope (maximum of
$U_{\infty }$. In particular, figure 10 shows the velocity of the WP in our simulation. In this figure we denote the time when the maximum value of the envelope (maximum of ![]() $|u_{WP}(t,x)|$) occurs at each downstream location of the sensors. The slope of the linear function fitting the three points on the
$|u_{WP}(t,x)|$) occurs at each downstream location of the sensors. The slope of the linear function fitting the three points on the ![]() $t$–
$t$–![]() $x$ plane represents the speed of the WP travelling in the streamwise direction, which, in our simulation, is 2.1901 m s
$x$ plane represents the speed of the WP travelling in the streamwise direction, which, in our simulation, is 2.1901 m s![]() $^{-1}$.
$^{-1}$.

Figure 10. Plot of ![]() $\arg \max |u_{WP}(t,L_x)|$ for each sensor on the
$\arg \max |u_{WP}(t,L_x)|$ for each sensor on the ![]() $t$–
$t$–![]() $x$ domain, where
$x$ domain, where ![]() $x$ is the distance from the leading edge and
$x$ is the distance from the leading edge and ![]() $t_0$ is the pulse start time. The slope of the fitted linear function represents the envelope velocity of the WP source.
$t_0$ is the pulse start time. The slope of the fitted linear function represents the envelope velocity of the WP source.
The sensors are located at ![]() $ {\boldsymbol {r}}_{x_1}= [796, \ 0]$ mm,
$ {\boldsymbol {r}}_{x_1}= [796, \ 0]$ mm, ![]() $ {\boldsymbol {r}}_{x_2} = [[l_x]_{x_1} + 6, \ 5]$ mm and
$ {\boldsymbol {r}}_{x_2} = [[l_x]_{x_1} + 6, \ 5]$ mm and ![]() $ {\boldsymbol {r}}_{x_3} =[[l_x]_{x_1} + 9, \ 5]$ mm. They are placed at the same height above the plate, near the outer maximum of the streamwise component of the TS disturbance profiles.
$ {\boldsymbol {r}}_{x_3} =[[l_x]_{x_1} + 9, \ 5]$ mm. They are placed at the same height above the plate, near the outer maximum of the streamwise component of the TS disturbance profiles.
The eigenfunction profiles (amplitude and phase of the streamwise disturbance velocities) of the two TS waves are shown in figure 11, where the sensors’ height above the plate is indicated by the horizontal line. As demonstrated in figure 11(b), each TS source has a vertical phase profile, with two distinct regions (near and away from the surface) separated by a jump with a value of ![]() ${\rm \pi}$. This jump occurs approximately between the inner and outer maximum of the eigenfunction amplitude profile (figure 11a).
${\rm \pi}$. This jump occurs approximately between the inner and outer maximum of the eigenfunction amplitude profile (figure 11a).

Figure 11. Streamwise component (![]() $u$) of TS sources:
$u$) of TS sources: ![]() $s_2$ (red) and
$s_2$ (red) and ![]() $s_3$ (magenta). (a) Eigenfunction amplitude (normalized by its maximum) and (b) eigenfunction phase. The sensors’ vertical position is denoted by the horizontal black dashed line.
$s_3$ (magenta). (a) Eigenfunction amplitude (normalized by its maximum) and (b) eigenfunction phase. The sensors’ vertical position is denoted by the horizontal black dashed line.
The phase profile of each source can result in false velocity angle estimation, because the phase change between the sensors is attributed to the source's horizontal propagation behaviour in our modelling framework. To overcome this problem, the sensors should be placed either (1) at the same height, outside or inside the boundary layer, e.g. near the inner maximum of the disturbance streamwise velocity profile (for non-parallel flow this height should be updated along the constant streamline), or (2) in the outer part of the boundary layer (if known a priori), possibly at different heights, where the phase profile is constant.
Using DUET for disturbance velocity estimation, which is the focus of the present example, is a two-stage procedure, with the first stage consisting of disturbance separation and identification. Since the theory underlying this stage has been thoroughly exemplified via the previous example, we defer the details concerning this stage to Appendix A. Thus, in the following, we only address the results of the second stage of the velocity estimation procedure, relying on the results of the first stage as they are described in Appendix A.
In figure 12 we overlay the histogram obtained using sensors 1 and 3 (blue contours) over the histogram obtained using sensors 1 and 2 (black contours). As can be clearly observed, the blue contours are shifted to the right relative to the black ones, that is, ![]() $|\delta _{j12}| < |\delta _{j13}|$, which agrees with the position of sensor 3 being downstream of sensor 2.
$|\delta _{j12}| < |\delta _{j13}|$, which agrees with the position of sensor 3 being downstream of sensor 2.

Figure 12. Top view of DUET two-dimensional cross power weighted (![]() $p = 1$,
$p = 1$, ![]() $q = 0$) histograms of symmetric attenuation (
$q = 0$) histograms of symmetric attenuation (![]() $\alpha = a - 1/a$) and delay estimate pairs. The histogram computed using sensors 1 and 3 (blue contours) is overlaid on the histogram computed using sensors 1 and 2 (black contours). The corresponding true (LST-computed) values of the mixing-parameter pairs of TS sources
$\alpha = a - 1/a$) and delay estimate pairs. The histogram computed using sensors 1 and 3 (blue contours) is overlaid on the histogram computed using sensors 1 and 2 (black contours). The corresponding true (LST-computed) values of the mixing-parameter pairs of TS sources ![]() $s_2$ (red) and
$s_2$ (red) and ![]() $s_3$ (magenta) are denoted by circles for sensors 1 and 2, and by squares for sensors 1 and 3. (For an isometric view and additional view angles, see figure 27 in Appendix A.).
$s_3$ (magenta) are denoted by circles for sensors 1 and 2, and by squares for sensors 1 and 3. (For an isometric view and additional view angles, see figure 27 in Appendix A.).
Next, we use the source delays, estimated from both histograms, to evaluate the corresponding velocity vector magnitude and direction by applying the method described in § 3. The resulting estimates are compared with the true values graphically in figure 13 and numerically in table 2.

Figure 13. (a) The DUET-estimated versus (b) true (LST-simulated) source velocities (speeds in m s![]() $^{-1}$ and direction angles in degrees):
$^{-1}$ and direction angles in degrees): ![]() $s_1$, blue;
$s_1$, blue; ![]() $s_2$, red;
$s_2$, red; ![]() $s_3$, magenta. The regions of
$s_3$, magenta. The regions of ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}>50$ are denoted by red dots.
${\kappa ({\boldsymbol{\mathsf{W}}})}>50$ are denoted by red dots.
Table 2. Estimated versus true disturbance velocities.
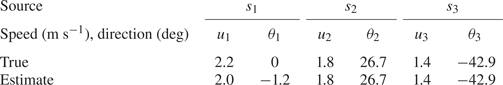
As can be observed, the estimated magnitudes and direction angles of the two TS sources are in excellent agreement with the true values, obtained via LST simulation, whereas the estimates corresponding to the WP source exhibit moderate errors. These estimation errors can be attributed, in part, to our choice to compare the estimates to the WP group velocity, because of its dispersive nature. Another factor that can contribute to the estimation errors is the smoothing resolution of the DUET histogram (![]() $\varDelta _\alpha$ and
$\varDelta _\alpha$ and ![]() $\varDelta _\delta$), used in (2.17) to determine the mixing parameters. We tune this resolution so as to bear a negligible impact on the estimates of the magnitude and direction of the velocity vector.
$\varDelta _\delta$), used in (2.17) to determine the mixing parameters. We tune this resolution so as to bear a negligible impact on the estimates of the magnitude and direction of the velocity vector.
5. Experimental study
We tested the method's performance using experimental data involving disturbance source mixtures in a boundary layer over a flat plate. The experiments were performed using a closed-loop wind tunnel at the Wind Tunnel Complex of Technion's aerospace engineering department. The tunnel has a concentration ratio of 5.76:1 and a test section cross-sectional area of 0.5 m by 0.5 m, and a length of 1.37 m. The plate dimensions are 0.45 m in width and 1.4 m in length. The trailing edge flap is 15 % of the total length of the plate. The free-stream velocity ![]() $U_{\infty }$ is set in the range 4–5 m s
$U_{\infty }$ is set in the range 4–5 m s![]() $^{-1}$, the flow over the plate is laminar and the free-stream turbulence intensity level does not exceed 0.15 %. A single dielectric barrier discharge (SDBD) plasma actuator (Moreau Reference Moreau2007; Corke, Post & Orlov Reference Corke, Post and Orlov2009) and a loudspeaker are used for the generation of artificial disturbances. The streamwise velocity measurements above the plate are obtained with the aid of two hot-wire anemometers, which we set to acquire data over a 6 s time interval at a 5 kHz sampling rate. The measured signal is first preprocessed before applying the DUET method, to remove possible contamination from the mixtures resulting from free-stream turbulence, background noise and slow base flow variations. More details of the experimental set-up and the signal processing procedures are provided in Appendices B and C, respectively.
$^{-1}$, the flow over the plate is laminar and the free-stream turbulence intensity level does not exceed 0.15 %. A single dielectric barrier discharge (SDBD) plasma actuator (Moreau Reference Moreau2007; Corke, Post & Orlov Reference Corke, Post and Orlov2009) and a loudspeaker are used for the generation of artificial disturbances. The streamwise velocity measurements above the plate are obtained with the aid of two hot-wire anemometers, which we set to acquire data over a 6 s time interval at a 5 kHz sampling rate. The measured signal is first preprocessed before applying the DUET method, to remove possible contamination from the mixtures resulting from free-stream turbulence, background noise and slow base flow variations. More details of the experimental set-up and the signal processing procedures are provided in Appendices B and C, respectively.
In what follows we present the results of two experiments. In the first we employ DUET to separate two disturbance sources using two sensors at different heights. The second experiment demonstrates how our DUET-based method, presented in § 2, can be used to estimate the velocities (magnitudes and directions) of mixed disturbance sources using a configuration of three sensors located at the same height.
5.1. Experiment 1: blind disturbance separation with two sensors
The set-up of the first experiment is shown in figure 14. An SDBD plasma actuator and a loudspeaker are used to generate two sources introduced upstream of the two hot-wire sensors, creating, in each sensor, a mixture comprising a TS wave and a WP. Specifically, placed outside the test section of the wind tunnel, the loudspeaker generates ![]() $s_1$, a single 60 Hz frequency disturbance (TS wave). Mounted on the plate 0.3 m downstream of the leading edge, the SDBD plasma actuator is used to generate
$s_1$, a single 60 Hz frequency disturbance (TS wave). Mounted on the plate 0.3 m downstream of the leading edge, the SDBD plasma actuator is used to generate ![]() $s_2$, a two-dimensional WP, being actuated via a 50 ms pulse signal. The free-stream velocity is set to 4.1 m s
$s_2$, a two-dimensional WP, being actuated via a 50 ms pulse signal. The free-stream velocity is set to 4.1 m s![]() $^{-1}$. The sensors are positioned at 0.775 and 0.78 m downstream from the leading edge, with a 40 mm spanwise separation between them. Sensors 1 and 2 are placed at heights that correspond to 0.19
$^{-1}$. The sensors are positioned at 0.775 and 0.78 m downstream from the leading edge, with a 40 mm spanwise separation between them. Sensors 1 and 2 are placed at heights that correspond to 0.19![]() $U_\infty$ and 0.23
$U_\infty$ and 0.23![]() $U_\infty$, respectively (for sensor 2, this value is obtained at
$U_\infty$, respectively (for sensor 2, this value is obtained at ![]() $y=0.77$ mm).
$y=0.77$ mm).

Figure 14. Flow over a flat plate with two disturbance generators: ![]() $s_1$ (loudspeaker source) and
$s_1$ (loudspeaker source) and ![]() $s_2$ (plasma actuator source); and two hot-wire sensors:
$s_2$ (plasma actuator source); and two hot-wire sensors: ![]() $x_1$ and
$x_1$ and ![]() $x_2$. Experimental set-up sketch.
$x_2$. Experimental set-up sketch.
Figures 15(a) and 15(d) display the streamwise velocity components, measured by two hot-wire sensors, after these signals are conditioned as described in Appendix C. The corresponding Fourier transforms are shown in figures 15(b) and 15(e), and the spectrograms of the mixtures are shown in figures 15(c) and 15(f), respectively. Figures 15(b) and 15(e) demonstrate that the dominant frequencies are, indeed, strongly related to the introduced sources. The bell-shaped signature of the WP has a dominant frequency of about 30 Hz, whereas the second source, generated by the loudspeaker, appears as a single-amplitude peak at 60 Hz. In addition, using a logarithmic scale in figures 15(c) and 15(f) reveals the weak presence of frequencies associated with experimental artifacts and the presence of noise in both mixtures. These were not removed by the signal preprocessing, because of their frequency-domain overlap with the sources comprising the mixture.

Figure 15. Mixtures as measured by two sensors: (a) ![]() $x_1$ and (d)
$x_1$ and (d) ![]() $x_2$. Corresponding Fourier transforms: (b)
$x_2$. Corresponding Fourier transforms: (b) ![]() $E_{x_1}$ and (e)
$E_{x_1}$ and (e) ![]() $E_{x_2}$. Corresponding spectrograms (dB), for which a window of 512 ms is used: (c)
$E_{x_2}$. Corresponding spectrograms (dB), for which a window of 512 ms is used: (c) ![]() $|\hat {x}_1|$ and (f)
$|\hat {x}_1|$ and (f) ![]() $|\hat {x}_2|$.
$|\hat {x}_2|$.
Figure 16 shows that the DUET-based method successfully identifies the correct number of introduced sources. The isometric view of the histogram, presented in figure 16(b), shows two peaks associated with two true TS and WP sources. Figure 16(a) displays the peak contours located around a mixing-parameter pair ![]() $(\alpha ,\delta )_1 = (1.3,-3\ \text {ms})$, whereas the WP peak contours are located at
$(\alpha ,\delta )_1 = (1.3,-3\ \text {ms})$, whereas the WP peak contours are located at ![]() $(\alpha ,\delta )_2=(-0.8,3.5\ \text {ms})$. The estimated delay parameter of the WP source, along with the known sensor downstream position, enable finding the WP envelope velocity:
$(\alpha ,\delta )_2=(-0.8,3.5\ \text {ms})$. The estimated delay parameter of the WP source, along with the known sensor downstream position, enable finding the WP envelope velocity: ![]() $c_g\approx ({l_{x_1}-l_{x_2}})/{\delta _2}=5/3.5=1.43$ m s
$c_g\approx ({l_{x_1}-l_{x_2}})/{\delta _2}=5/3.5=1.43$ m s![]() $^{-1}$, which is
$^{-1}$, which is ![]() $0.36U$, where
$0.36U$, where ![]() $U$ is the free-stream velocity. This result is in agreement with the analysis presented in (Gaster & Grant Reference Gaster and Grant1975), according to which the leading edge of the WP envelope in a BBL propagates at a velocity of
$U$ is the free-stream velocity. This result is in agreement with the analysis presented in (Gaster & Grant Reference Gaster and Grant1975), according to which the leading edge of the WP envelope in a BBL propagates at a velocity of ![]() $0.44U_\infty$, whereas the trailing edge of the envelope propagates at
$0.44U_\infty$, whereas the trailing edge of the envelope propagates at ![]() $0.36U_\infty$.
$0.36U_\infty$.

Figure 16. A DUET two-dimensional cross power weighted ![]() $(p = 1, q = 0)$ histogram of symmetric attenuation
$(p = 1, q = 0)$ histogram of symmetric attenuation ![]() $\alpha =(a - 1/a)$ and delay estimate pairs from two mixtures of two sources. (a) Contour plot of the two-dimensional histogram. (b) Isometric view.
$\alpha =(a - 1/a)$ and delay estimate pairs from two mixtures of two sources. (a) Contour plot of the two-dimensional histogram. (b) Isometric view.
Obtained from the histogram peak locations, the identified mixing parameters are used to demix the sources. Figure 17 shows the two estimated sources as identified by the DUET method. Figures 17(a) and 17(d) clearly feature typical TS and WP time signatures, respectively. The noise, which is evident in the spectrograms of the measured mixtures in figure 15, is also evident in the spectrograms of the identified sources in figure 17. Nevertheless, the unique signature of each source is almost uncontaminated by that of the other source, indicating that the DUET method is robust with respect to low noise contamination levels that are hard to avoid in experiments.

Figure 17. The DUET estimates of sources: (a) ![]() $y_1$ and (d)
$y_1$ and (d) ![]() $y_2$. Corresponding Fourier transforms: (b)
$y_2$. Corresponding Fourier transforms: (b) ![]() $E_{y_1}$ and (e)
$E_{y_1}$ and (e) ![]() $E_{y_2}$. Corresponding spectrograms (dB): (c)
$E_{y_2}$. Corresponding spectrograms (dB): (c) ![]() $|\hat {y}_1|$ and (f)
$|\hat {y}_1|$ and (f) ![]() $|\hat {y}_2|$.
$|\hat {y}_2|$.
This experimental example demonstrates that the DUET method performs well as a source identification and separation method, when applied to disturbances acting in a transitional boundary layer. We have obtained similar results in other experiments, under different mixing scenarios.
5.2. Experiment 2: disturbance velocity estimation
This experiment tests the performance of our DUET-based disturbance propagation velocity estimator. The experimental set-up is almost identical to the one described in § 5.1, except that, instead of using a loudspeaker, an additional plasma actuator is used to generate the second source, as depicted in figure 18. The two SDBD plasma actuators are mounted such that one is placed spanwise parallel to the leading edge and located at ![]() $x=300$ mm downstream from the plate's leading edge, whereas the other is inclined at
$x=300$ mm downstream from the plate's leading edge, whereas the other is inclined at ![]() $15^\circ$ to the leading edge, and its centre (
$15^\circ$ to the leading edge, and its centre (![]() $z=0$ mm) is located at
$z=0$ mm) is located at ![]() $x=500$ mm. The inclined actuator can generate oblique TS wave or WP disturbances.
$x=500$ mm. The inclined actuator can generate oblique TS wave or WP disturbances.

Figure 18. Experimental set-up of flow over a flat plate equipped with two active plasma actuators. (a) Photo of experimental set-up and (b) schematic diagram of experimental set-up. The region of the hot-wire sensors position is denoted by the magenta square.
The two SDBD actuators are used to introduce two disturbances into the boundary layer. The plasma actuator parallel to the leading edge is used to generate ![]() $s_1$, a two-dimensional WP source, travelling downstream at
$s_1$, a two-dimensional WP source, travelling downstream at ![]() $\theta =0^\circ$ (so that
$\theta =0^\circ$ (so that ![]() $\beta _0=0$, by (4.15)). The inclined plasma actuator is used to generate
$\beta _0=0$, by (4.15)). The inclined plasma actuator is used to generate ![]() $s_2$, an oblique WP source, travelling downstream at
$s_2$, an oblique WP source, travelling downstream at ![]() $\theta \approx -15^\circ$. Both actuators are driven by a single, 10 ms pulse, such that the actuator parallel to the leading edge is delayed by 10 ms with respect to the other, to render both sources distinguishable in the time–frequency domain. To ensure linear interactions, both actuators are driven by the smallest voltage that still generates uniform discharge along the actuator span.
$\theta \approx -15^\circ$. Both actuators are driven by a single, 10 ms pulse, such that the actuator parallel to the leading edge is delayed by 10 ms with respect to the other, to render both sources distinguishable in the time–frequency domain. To ensure linear interactions, both actuators are driven by the smallest voltage that still generates uniform discharge along the actuator span.
The free-stream velocity ![]() $U_{\infty }$ is set to 5 m s
$U_{\infty }$ is set to 5 m s![]() $^{-1}$. All sensors are placed at 0.5 mm height above the plate's surface, rendering a measured mean streamwise velocity of 0.27
$^{-1}$. All sensors are placed at 0.5 mm height above the plate's surface, rendering a measured mean streamwise velocity of 0.27![]() $U_\infty$ at that height. Three sensor configurations, shown in figure 19 and termed ‘asymmetric’, ‘singular’ and ‘symmetric’, are tested (see Appendix B.4 for the technique used to realize a three-sensor configuration using only two hot wires). In each configuration the sensors are located at the central region of the plate, and the fixed sensor (sensor 1) is placed at
$U_\infty$ at that height. Three sensor configurations, shown in figure 19 and termed ‘asymmetric’, ‘singular’ and ‘symmetric’, are tested (see Appendix B.4 for the technique used to realize a three-sensor configuration using only two hot wires). In each configuration the sensors are located at the central region of the plate, and the fixed sensor (sensor 1) is placed at ![]() $ {\boldsymbol {r}}_{x_1}=[643, \ 25]$ mm. The small variations in sensor pair locations between the configurations, as shown in figure 19, translate to different source arrival times at the sensors.
$ {\boldsymbol {r}}_{x_1}=[643, \ 25]$ mm. The small variations in sensor pair locations between the configurations, as shown in figure 19, translate to different source arrival times at the sensors.

Figure 19. Top (![]() $x$–
$x$–![]() $z$ plane) view of three studied sensor configurations relative to
$z$ plane) view of three studied sensor configurations relative to ![]() $ {\boldsymbol {r}}_{x_1}=[643,\ 25]$ mm (at the origin). The sensors are denoted by symbols:
$ {\boldsymbol {r}}_{x_1}=[643,\ 25]$ mm (at the origin). The sensors are denoted by symbols: ![]() $\times$, sensor 1 (master); circle, sensor 2 (slave); square, sensor 3 (slave). Baselines are denoted by arrows. (a) Asymmetric configuration, (b) singular configuration and (c) symmetric configuration.
$\times$, sensor 1 (master); circle, sensor 2 (slave); square, sensor 3 (slave). Baselines are denoted by arrows. (a) Asymmetric configuration, (b) singular configuration and (c) symmetric configuration.
Typical mixtures, measured by sensors 1 and 3 in the asymmetric configuration, are shown in figure 20. The presence of both WP sources is evident in both measured mixtures. The corresponding DUET-estimated sources are shown in figure 21, which demonstrates effective source separation. Similar results, not shown here for conciseness, were obtained for the singular and symmetric sensor configurations.

Figure 20. Mixtures as measured by two sensors for the asymmetric configuration: (a) ![]() $x_1$ and (d)
$x_1$ and (d) ![]() $x_3$. Corresponding Fourier transforms: (b)
$x_3$. Corresponding Fourier transforms: (b) ![]() $E_{x_1}$ and (e)
$E_{x_1}$ and (e) ![]() $E_{x_3}$. Corresponding spectrograms (dB), for which a window of 128 ms is used: (c)
$E_{x_3}$. Corresponding spectrograms (dB), for which a window of 128 ms is used: (c) ![]() $|\hat {x}_1|$ and (f)
$|\hat {x}_1|$ and (f) ![]() $|\hat {x}_3|$.
$|\hat {x}_3|$.

Figure 21. The DUET estimates of sources using sensors 1 and 3 in asymmetric configuration: (a) ![]() $y_1$ and (d)
$y_1$ and (d) ![]() $y_2$. Corresponding Fourier transforms: (b)
$y_2$. Corresponding Fourier transforms: (b) ![]() $E_{y_1}$ and (e)
$E_{y_1}$ and (e) ![]() $E_{y_2}$. Corresponding spectrograms (dB): (c)
$E_{y_2}$. Corresponding spectrograms (dB): (c) ![]() $|\hat {y}_1|$ and (f)
$|\hat {y}_1|$ and (f) ![]() $|\hat {y}_2|$.
$|\hat {y}_2|$.
For each of the three sensor configurations, we overlay, in figure 22, the histogram obtained by using sensors 1 and 3 (blue contours) on the histogram obtained by using sensors 1 and 2 (black contours). As can be clearly observed, the black contours are shifted to the right relative to the blue ones, that is, ![]() $|\delta _{j13}| < |\delta _{j12}|$, which agrees with the position of sensor 2 being downstream of sensor 3 in all three configurations.
$|\delta _{j13}| < |\delta _{j12}|$, which agrees with the position of sensor 2 being downstream of sensor 3 in all three configurations.

Figure 22. Top view of DUET two-dimensional cross power weighted (![]() $p = 1$,
$p = 1$, ![]() $q = 0$) histograms for the studied three-sensor configurations. The histogram computed using sensors 1 and 3 (blue contours) is overlaid on the histogram computed using sensors 1 and 2 (black contours). (a) Asymmetric configuration, (b) singular configuration and (c) symmetric configuration.
$q = 0$) histograms for the studied three-sensor configurations. The histogram computed using sensors 1 and 3 (blue contours) is overlaid on the histogram computed using sensors 1 and 2 (black contours). (a) Asymmetric configuration, (b) singular configuration and (c) symmetric configuration.
Next, we use the source delays, estimated from both histograms, to evaluate the corresponding velocity vector magnitude and direction by applying the method of § 3. These estimates are shown graphically in figure 23 and summarized numerically in table 3, for each of the tested sensor configurations.

Figure 23. Estimated velocities of sources ![]() $s_1$ (blue) and
$s_1$ (blue) and ![]() $s_2$ (red) using the three studied sensor configurations. (a) Asymmetric configuration, (b) singular configuration and (c) symmetric configuration. The regions of
$s_2$ (red) using the three studied sensor configurations. (a) Asymmetric configuration, (b) singular configuration and (c) symmetric configuration. The regions of ![]() ${\kappa ({\boldsymbol{\mathsf{W}}})}>50$ are denoted by red dots.
${\kappa ({\boldsymbol{\mathsf{W}}})}>50$ are denoted by red dots.
Table 3. Estimated source velocities.

The results show that the streamwise-travelling two-dimensional WP disturbance is estimated quite consistently by all three sensor configurations. The oblique WP estimates, on the other hand, exhibit a substantially larger variation. Nevertheless, the estimated WP envelope velocities of both sources are between ![]() $0.3U_{\infty }$ and
$0.3U_{\infty }$ and ![]() $0.45U_{\infty }$, which are close to the values of our numerical example (see § 4.6).
$0.45U_{\infty }$, which are close to the values of our numerical example (see § 4.6).
The discrepancy of about ![]() $3^\circ$ between the estimated
$3^\circ$ between the estimated ![]() $\theta _1$ and the
$\theta _1$ and the ![]() $0^\circ$ angle of the parallel actuator (that created it) can be attributed to several factors: (1) an imperfect alignment of the sensor on the
$0^\circ$ angle of the parallel actuator (that created it) can be attributed to several factors: (1) an imperfect alignment of the sensor on the ![]() $x$–
$x$–![]() $z$ plane (the positioning accuracy was 1 mm), (2) random artifacts, caused by the fact that two repeated experiments had to be done to obtain the required three sensor measurements with only two sensors, (3) DUET histogram resolution (although this resolution was tuned to bear a negligible impact on the estimates of the velocity vector), (4) the disturbance can, potentially, not precisely adhere to the inclination angle of its generating actuator when propagating downstream and (5) slight variations in the phase profiles may exist, in particular for the
$z$ plane (the positioning accuracy was 1 mm), (2) random artifacts, caused by the fact that two repeated experiments had to be done to obtain the required three sensor measurements with only two sensors, (3) DUET histogram resolution (although this resolution was tuned to bear a negligible impact on the estimates of the velocity vector), (4) the disturbance can, potentially, not precisely adhere to the inclination angle of its generating actuator when propagating downstream and (5) slight variations in the phase profiles may exist, in particular for the ![]() $s_1$ WP. In what follows, we examine the latter two factors in further detail.
$s_1$ WP. In what follows, we examine the latter two factors in further detail.
To investigate how the generated disturbance changes its inclination angle as it propagates downstream from its generating actuator, we track the temporal evolution of a localized disturbance within the boundary layer over a flat plate. Figure 24 shows the time history of the streamwise velocity of the disturbances as they pass through two points, located at 600 and 650 mm from the leading edge, both at a height of ![]() $y=0.9$ mm above the plate. Consisting of
$y=0.9$ mm above the plate. Consisting of ![]() $10^3$ points, the velocity record is digitized at 1 kHz, such that the total measuring time is 1 s for each
$10^3$ points, the velocity record is digitized at 1 kHz, such that the total measuring time is 1 s for each ![]() $(x,y,z)$ location. The measurement sequence is synchronized by a pulse from the computer that triggers the disturbance generator. The inclined actuator, which generates
$(x,y,z)$ location. The measurement sequence is synchronized by a pulse from the computer that triggers the disturbance generator. The inclined actuator, which generates ![]() $s_2$, and the parallel actuator, which generates
$s_2$, and the parallel actuator, which generates ![]() $s_1$, are triggered 0.2 and 0.5 s after the beginning of the recording, respectively. At each measuring point, an ensemble average of six realizations of the disturbance passage is computed (this number of realizations was found to be sufficient to adequately represent the flow structure).
$s_1$, are triggered 0.2 and 0.5 s after the beginning of the recording, respectively. At each measuring point, an ensemble average of six realizations of the disturbance passage is computed (this number of realizations was found to be sufficient to adequately represent the flow structure).

Figure 24. Time histories of streamwise disturbance velocity at two downstream stations. (a) Colourbar for (b,c). Time history of streamwise disturbance velocity at (b) ![]() $y=0.9$ mm,
$y=0.9$ mm, ![]() $x=600$ mm and (c)
$x=600$ mm and (c) ![]() $y=0.9$ mm,
$y=0.9$ mm, ![]() $x=650$ mm. (d) Pulsation sequence of actuator parallel to leading edge (blue) and inclined actuator (red). Free-stream velocity is
$x=650$ mm. (d) Pulsation sequence of actuator parallel to leading edge (blue) and inclined actuator (red). Free-stream velocity is ![]() $U=5$ m s
$U=5$ m s![]() $^{-1}$. In (b,c) the estimated values of WP envelope inclination angles are denoted by the red (
$^{-1}$. In (b,c) the estimated values of WP envelope inclination angles are denoted by the red (![]() $s_2$) and blue (
$s_2$) and blue (![]() $s_1$) lines.
$s_1$) lines.
In figure 24 the WP propagation angle at both measuring points is evident within the central region, where the boundary layer maintains its laminarity and is not affected by the spanwise edges of the plate. Assuming that the propagation angles remain fixed from disturbance generation until the mixtures reach the sensors, we use the estimated angles from table 3 to plot the estimated wavefront inclination angle in the ![]() $t$–
$t$–![]() $z$ domain over the measured time history of the flow. As figure 24 clearly shows, the inclined WP source,
$z$ domain over the measured time history of the flow. As figure 24 clearly shows, the inclined WP source, ![]() $s_2$, is estimated very well, and better than the WP source
$s_2$, is estimated very well, and better than the WP source ![]() $s_1$. This is most likely due to the phase changes of
$s_1$. This is most likely due to the phase changes of ![]() $s_1$ at the sampled locations.
$s_1$ at the sampled locations.
To determine if there are slight variations in the disturbance phase profiles, we plot in figure 25(a) the same time histories used to obtain figure 24(c), on the ![]() $t$–
$t$–![]() $y$ domain, at
$y$ domain, at ![]() $x=600$ mm and
$x=600$ mm and ![]() $z = 0$ mm. The free-stream velocity is
$z = 0$ mm. The free-stream velocity is ![]() $U=5$ m s
$U=5$ m s![]() $^{-1}$. The signals are normalized by their maximal values to make them more pronounced. In figure 25(b) we show the mean profile of the flow without actuation at the same location, in order to reference the sensor heights to the canonical boundary layer at that location. Some slight non-coherence in the shape of source
$^{-1}$. The signals are normalized by their maximal values to make them more pronounced. In figure 25(b) we show the mean profile of the flow without actuation at the same location, in order to reference the sensor heights to the canonical boundary layer at that location. Some slight non-coherence in the shape of source ![]() $s_1$ is evident below the height of 1 mm (which is below 0.35
$s_1$ is evident below the height of 1 mm (which is below 0.35![]() $U_\infty$), indicating disturbance phase variations at that region. Thus, placing sensors at that height reduces our method's precision in estimating the velocity vector of source
$U_\infty$), indicating disturbance phase variations at that region. Thus, placing sensors at that height reduces our method's precision in estimating the velocity vector of source ![]() $s_1$.
$s_1$.

Figure 25. (a) Time history of disturbance streamwise velocity on the ![]() $t$–
$t$–![]() $y$ domain and (b) mean flow profile without actuation, both obtained at
$y$ domain and (b) mean flow profile without actuation, both obtained at ![]() $x=600$ mm and
$x=600$ mm and ![]() $z=0$ mm, for
$z=0$ mm, for ![]() $U_\infty =5$ m s
$U_\infty =5$ m s![]() $^{-1}$.
$^{-1}$.
6. Concluding remarks
This paper presents a novel approach for the isolation and identification of disturbances in a boundary layer. Enabling this approach, the model adopted in this work regards the flow state as an unknown mixture of disturbance sources. The primary goal of the study is to identify the flow physics, or, in terms of our model, the mixing process, based on information acquired using a limited number of sensors embedded in the flow.
Because the number of disturbances and their mixing parameters in the boundary layer are a priori unknown, we use DUET as a BSS mechanism to reconstruct the separate sources and their mixing process. Only two sensors, as a minimum, are required for this source separation and identification, and this number is independent of the number of disturbances active in the flow. Adding an additional sensor, and complying with some physics-based design rules, we also present a method, motivated by techniques for GPS-based spacecraft attitude determination, to determine the propagation velocity vector (magnitude and direction) of each of the sources, based on readings of only three sensors appropriately positioned in the flow field.
We demonstrate our methods both numerically and experimentally. The numerical study employs LST to model the source mixtures acquired by sensors placed in a BBL. We consider three-dimensional TS waves and WPs, which may propagate downstream along with the free-stream direction or at a certain angle with respect to it. Carried out in a wind tunnel, the experimental study considers flow over a flat plate, with hot wires as sensors and a loudspeaker and plasma actuators as source generators.
Both numerical and experimental studies demonstrate the robustness of the DUET-based method with respect to the validity of its underlying assumptions. This is especially true in the experimental domain, where these assumptions are more challenging to satisfy, because of sensor positioning and alignment errors, random artifacts and measurement noises. In particular, we demonstrate how DUET can separate sources that coexist over some time–frequency interval, i.e. when the set-up does not fully comply with the source sparsity (WDO) assumption, which is one of DUET's underlying assumptions.
Our novel identification and isolation scheme may be used to provide new insights and perspectives on how transitional flows can be studied. The information gained concerning sources and their mixing parameters may provide essential insights into the physical fluid system, and information on aspects of the flow that can be relevant from control perspectives.
Acknowledgements
The authors wish to thank the following individuals: O. Kan and Y. Shulman, research engineers of the Turbulence Lab of Technion's Faculty of Aerospace Engineering, for their assistance in designing and constructing the experimental set-up; the staff of the Wind Tunnel Complex of Technion's Faculty of Aerospace Engineering, in particular M. Koifman, G. Benski, O. Borochovich, D. Baraki and N. Shefer, for their vital technical support; D. Simon, of Technion's UAV Workshop, for his assistance in manufacturing the leading edge; and D. Greenblatt, of Technion's Faculty of Mechanical Engineering, and D. Ashpis of NASA, Cleveland, Ohio, for their professional advice regarding plasma actuator construction and operation.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Disturbance separation with two sensors (example 2 in § 4.6)
In this appendix we provide details pertaining to the application of DUET for source separation in example 2 of § 4.6. Figures 26(a), 26(d) and 26(g) display the time behaviour of the mixtures over the time interval ![]() $[0.2, 0.6]$ s. The corresponding Fourier transforms are shown in figures 26(b), 26(e) and 26(h), from which it can be seen that each mixture contains the frequencies of all introduced sources. Each TS source has a unique single frequency, whereas the WP spectrum exhibits a typical bell-shaped signature with a maximum at about 90 Hz. The respective spectrograms of the mixtures in the time–frequency domain are shown in figures 26(c), 26(f) and 26(i).
$[0.2, 0.6]$ s. The corresponding Fourier transforms are shown in figures 26(b), 26(e) and 26(h), from which it can be seen that each mixture contains the frequencies of all introduced sources. Each TS source has a unique single frequency, whereas the WP spectrum exhibits a typical bell-shaped signature with a maximum at about 90 Hz. The respective spectrograms of the mixtures in the time–frequency domain are shown in figures 26(c), 26(f) and 26(i).

Figure 26. Time signatures as measured by the three sensors: (a) ![]() $x_1$, (d)
$x_1$, (d) ![]() $x_2$ and (g)
$x_2$ and (g) ![]() $x_3$. Respective Fourier transforms: (b)
$x_3$. Respective Fourier transforms: (b) ![]() $E_{x_1}$, (e)
$E_{x_1}$, (e) ![]() $E_{x_2}$ and (h)
$E_{x_2}$ and (h) ![]() $E_{x_3}$. Respective spectrograms (dB): (c)
$E_{x_3}$. Respective spectrograms (dB): (c) ![]() $|\hat x_1|$, (f)
$|\hat x_1|$, (f) ![]() $|\hat x_2|$ and (i)
$|\hat x_2|$ and (i) ![]() $|\hat x_3|$.
$|\hat x_3|$.
Figure 27 shows the histogram computed using the measurements of sensors 1 and 2. The isometric view of the histogram in figure 27(b) reveals three peaks associated with the three original sources: two TS sources and one WP source. In figure 27(a) we superimpose the mixing-parameter pairs of the TS sources, as computed by LST, over the histogram peak contours. Clearly, the histogram peaks coincide with the mixing parameters of the three LST-computed sources.

Figure 27. A DUET two-dimensional cross power weighted (![]() $p = 1$,
$p = 1$, ![]() $q = 0$) histogram using sensors 1 and 2. (a) Contour plot (black) of the histogram with corresponding true (LST-computed) mixing-parameter pairs for each TS source
$q = 0$) histogram using sensors 1 and 2. (a) Contour plot (black) of the histogram with corresponding true (LST-computed) mixing-parameter pairs for each TS source ![]() $s_2$ (red circle) and
$s_2$ (red circle) and ![]() $s_3$ (magenta circle). (b) Isometric view.
$s_3$ (magenta circle). (b) Isometric view.
The identified mixing parameters, obtained from the histogram peak locations, are used to demix the sources. Figure 28 shows the three DUET-estimated sources. The quality of the separation is manifested by the fact that the signature of each estimated source is uncontaminated by the other two sources.

Figure 28. The DUET estimates of sources using sensors 1 and 2: (a) ![]() $y_1$, (d)
$y_1$, (d) ![]() $y_2$ and (g)
$y_2$ and (g) ![]() $y_3$. Corresponding Fourier transforms: (b)
$y_3$. Corresponding Fourier transforms: (b) ![]() $E_{y_1}$, (e)
$E_{y_1}$, (e) ![]() $E_{y_2}$ and (h)
$E_{y_2}$ and (h) ![]() $E_{y_3}$. Corresponding spectrograms (dB): (c)
$E_{y_3}$. Corresponding spectrograms (dB): (c) ![]() $|\hat {y}_1|$, (f)
$|\hat {y}_1|$, (f) ![]() $|\hat {y}_2|$ and (i)
$|\hat {y}_2|$ and (i) ![]() $|\hat {y}_3|$ dB.
$|\hat {y}_3|$ dB.
Appendix B. Experimental set-up and data processing details
In this appendix we briefly describe the components of the experimental set-up.
B.1. Wind tunnel
The experiments are performed in a closed-loop wind tunnel with a contraction ratio of 5.76:1, a test cross-sectional area of 0.5 m by 0.5 m and a length of 1.37 m. The sidewalls of the test section are made of 10 mm thick transparent Perspex, with an adjustable angle to control the pressure gradient inside the test section. The air temperature is ![]() $20\pm 2\,^\circ$C. The air flow is driven by a vane-axial fan powered by a 15 kW motor, which is capable of generating a free-stream velocity up to 50 m s
$20\pm 2\,^\circ$C. The air flow is driven by a vane-axial fan powered by a 15 kW motor, which is capable of generating a free-stream velocity up to 50 m s![]() $^{-1}$ inside the test section. The tunnel is designed to have low turbulence levels (0.15 % at velocities up to 10 m s
$^{-1}$ inside the test section. The tunnel is designed to have low turbulence levels (0.15 % at velocities up to 10 m s![]() $^{-1}$ for a filtered range of 0.1–500 Hz). These low turbulence levels are achieved by placing corner vanes at each corner of the tunnel, and by positioning a settling chamber upstream of the converging nozzle that contains a honeycomb with a cell diameter of 5 mm, and four screens downstream of it.
$^{-1}$ for a filtered range of 0.1–500 Hz). These low turbulence levels are achieved by placing corner vanes at each corner of the tunnel, and by positioning a settling chamber upstream of the converging nozzle that contains a honeycomb with a cell diameter of 5 mm, and four screens downstream of it.
B.2. Flat plate
The boundary layer is formed along a flat plate made of three, combined, 4 mm thick glass sheets that satisfy a waviness criterion for plate surfaces used for stability experiments: ![]() $\varepsilon /{\lambda _{TS}}<10^{-3}$, where
$\varepsilon /{\lambda _{TS}}<10^{-3}$, where ![]() $\varepsilon$ is the height above the plate and
$\varepsilon$ is the height above the plate and ![]() $\lambda _{TS}$ is the TS wavelength (Saric Reference Saric2008). The leading edge has an asymmetric shape and is designed to minimize the adverse pressure gradient according to Fransson (Reference Fransson2004). The trailing edge is equipped with a flap having an adjustable angle, that enables control of the stagnation line at the leading edge, thereby preventing boundary layer separation there. The plate dimensions are 0.45 m in width and 1.4 m in length. The trailing edge flap is 15 % of the total length of the plate. A filling material (plasticine) is inserted between the various parts (the leading edge, plate and trailing edge flap) and covered by a single layer of Kapton tape in order to avoid junction discontinuities. The plate is mounted on a supporting frame, specially designed to minimize the test section area blockage. The front tip of the plate's leading edge is placed at the beginning of the test section, and the plate's top surface is positioned at mid-height of the test section.
$\lambda _{TS}$ is the TS wavelength (Saric Reference Saric2008). The leading edge has an asymmetric shape and is designed to minimize the adverse pressure gradient according to Fransson (Reference Fransson2004). The trailing edge is equipped with a flap having an adjustable angle, that enables control of the stagnation line at the leading edge, thereby preventing boundary layer separation there. The plate dimensions are 0.45 m in width and 1.4 m in length. The trailing edge flap is 15 % of the total length of the plate. A filling material (plasticine) is inserted between the various parts (the leading edge, plate and trailing edge flap) and covered by a single layer of Kapton tape in order to avoid junction discontinuities. The plate is mounted on a supporting frame, specially designed to minimize the test section area blockage. The front tip of the plate's leading edge is placed at the beginning of the test section, and the plate's top surface is positioned at mid-height of the test section.
B.3. Disturbance generators
SDBD plasma actuators and a loudspeaker are utilized for generation of controlled disturbances. The actuation signals for both are generated with the aid of LabVIEW software. Plasma actuators have been studied and used in a wide range of flow applications. Detailed reviews of plasma actuator physics, experiments and applications are given in Moreau (Reference Moreau2007), Corke et al. (Reference Corke, Post and Orlov2009) and Kriegseis, Simon & Grundmann (Reference Kriegseis, Simon and Grundmann2016).
We use copper tape (66 ![]() $\mathrm {\mu }$m thick and 10 mm wide) as the electrodes of the actuator, a glass sheet (4 mm thick) as the dielectric insulation between the electrodes and Kapton tape for encapsulation of the grounded electrode. The actuation signal is generated by a GBS MiniPuls 2.1 kit that consists of two boards: (1) a full-bridge converter and (2) a transformer cascade (RM14). The assembly can generate high AC voltages with frequencies in the range 5–20 kHz, and amplitudes up to 10 kV (7
$\mathrm {\mu }$m thick and 10 mm wide) as the electrodes of the actuator, a glass sheet (4 mm thick) as the dielectric insulation between the electrodes and Kapton tape for encapsulation of the grounded electrode. The actuation signal is generated by a GBS MiniPuls 2.1 kit that consists of two boards: (1) a full-bridge converter and (2) a transformer cascade (RM14). The assembly can generate high AC voltages with frequencies in the range 5–20 kHz, and amplitudes up to 10 kV (7 ![]() $\textrm {kV}_\textrm {RMS}$). The system internal control allows adjusting the signal's burst frequency in the range 0–400 Hz, and has a duty cycle in the range 0 %–100 %.
$\textrm {kV}_\textrm {RMS}$). The system internal control allows adjusting the signal's burst frequency in the range 0–400 Hz, and has a duty cycle in the range 0 %–100 %.
A single DIBEISI difuzor loudspeaker, having a diameter of 200 mm, is used as an additional disturbance generator. The loudspeaker is placed outside the test section and away from the measuring system to prevent mechanical vibrations. The actuation input signal to the loudspeaker is a superposition of sine waves with maximum amplitudes of 3 V, amplified by a ![]() $-$10 dB gain via a MAX 860 power-amplifier capable of 300 W output. The generated acoustic waves create pressure disturbances that interact with the boundary layer.
$-$10 dB gain via a MAX 860 power-amplifier capable of 300 W output. The generated acoustic waves create pressure disturbances that interact with the boundary layer.
B.4. Sensors and data acquisition system
The velocity of the free stream entering the test section is measured by a Pitot tube connected to an MKS BARATRON model 398HD pressure transducer, mounted on top of the mid-spanwise part of the test section inlet plane. The streamwise velocity (above the plate) is measured with the aid of two hot wires (DANTEC, type 55P11) connected to a hot-wire anemometry system of A. A. Lab Systems. The straight, 5 ![]() $\mathrm {\mu }$m in diameter, tungsten hot-wire probes are kept at an overheat ratio of 1.6, corresponding to a maximal frequency response of 30 kHz. During calibration, each hot wire is placed adjacent to the Pitot tube. The calibration includes seven velocities in the range 0–10 m s
$\mathrm {\mu }$m in diameter, tungsten hot-wire probes are kept at an overheat ratio of 1.6, corresponding to a maximal frequency response of 30 kHz. During calibration, each hot wire is placed adjacent to the Pitot tube. The calibration includes seven velocities in the range 0–10 m s![]() $^{-1}$ at a temperature of 20
$^{-1}$ at a temperature of 20 ![]() $^\circ$C. The hot-wire anemometer and BARATRON pressure transducer data acquisition are controlled using a regular PC and LabVIEW software.
$^\circ$C. The hot-wire anemometer and BARATRON pressure transducer data acquisition are controlled using a regular PC and LabVIEW software.
During the measurement of the disturbance mixtures in the boundary layer, one hot wire is kept stationary, while the other is mounted on a three-axis traversing mechanism, with a resolution of 5 ![]() $\mathrm {\mu }$m in the wall-normal vertical direction and 1 mm in both the streamwise and spanwise directions. The positioning of the probe within the boundary layer at a given downstream station is controlled by the computer that drives the stepping motors through LabVIEW software.
$\mathrm {\mu }$m in the wall-normal vertical direction and 1 mm in both the streamwise and spanwise directions. The positioning of the probe within the boundary layer at a given downstream station is controlled by the computer that drives the stepping motors through LabVIEW software.
Our method requires the use of (at least) three sensors for reconstructing the velocity vectors of the sources. However, in our experiments, laboratory set-up limitations dictated the use of only a pair of hot wires. To circumvent this limitation, we used the following approach. One hot-wire sensor, designated as ‘master sensor 1’, was kept stationary throughout the entire experiment. The experiment was performed two times, where, in the first run, the traversed hot wire was used as ‘slave sensor 2’, in one location, and, in the second run, as ‘slave sensor 3’, in another location. This approach relies on the facts that (1) DUET can be used with only two sensors and (2) the initial phase of the sources in the mixture is irrelevant to our method. We assume that the mixing parameters (particularly the delay of arrival) of each source are the same between the repeated experiments. It should be noted, however, that this assumption can never be ideally realized in practice, so that the use of repeated experiments necessarily adversely affects the method's accuracy.
Appendix C. Signal preprocessing before applying DUET
Prior to applying our DUET-based method to the acquired signals, they are preprocessed according to the following consecutive steps.
(i) Prior to recording the signals, hardware low-pass filtering is applied, so that the filtered signals have a cutoff frequency of 1 kHz. This is done to eliminate the effects of electromagnetic interference, which is generated by the SDBD plasma actuator. The selected cutoff frequency does not detrimentally affect the measurements because the relevant boundary layer frequencies in this study are below 200 Hz.
(ii) Next, the signals are detrended to remove slow variations of the base flow with typical frequencies well below those of the introduced sources. Detrending is performed by subtracting from the signal a smoothed version of it, generated by applying a moving average operator to the measured signal. The smoothing window length of the moving average operator is set to smooth out short-term fluctuations of source mixtures and highlight the longer-term trends of the base flow. Detrending is done to ensure that the DUET-based method does not identify these slow variations as additional sources existing in the flow.
(iii) The detrended signals are then low-pass-filtered to remove artifacts and noise below 1 kHz that result from electrical devices, such as the traverse stepper motor noise and sensor noise, as well as from random flow events or truncation errors of the recorded signals. This procedure is done by applying to the recorded signal a moving average operator with a window length designed to ensure that the signal acquisition sample rate is as short as possible but sufficiently long to remove these artifacts.
(iv) Finally, we make sure that the detrended signals are centred by subtracting their computed means from them. This ensures the removal of the base flow profile effect on symmetric attenuation, which is based on the ratio between the absolute values of the sensor measurements. Therefore, by centring each measured signal, we ensure that the estimated symmetric attenuation would be within the predetermined limits of the DUET histogram, for appropriate source separation.