Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T06:02:29.887Z Has data issue: false hasContentIssue false
  • English
  • Français

Blood flow in small tubes: quantifying the transition to the non-continuum regime

Published online by Cambridge University Press:  28 March 2013

Huan Lei ,
Dmitry A. Fedosov ,
Bruce Caswell  and
George Em Karniadakis
Huan Lei
Affiliation:
Division of Applied Mathematics, Brown University, Providence, RI 02912, USA
Dmitry A. Fedosov
Affiliation:
Institute of Complex Systems and Institute for Advanced Simulation, Forschungszentrum Jülich, 52425 Jülich, Germany
Bruce Caswell
Affiliation:
School of Engineering, Brown University, Providence, RI 02912, USA
George Em Karniadakis*
Affiliation:
Division of Applied Mathematics, Brown University, Providence, RI 02912, USA
*
†Email address for correspondence: george_karniadakis@brown.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In small vessels blood is usually treated as a Newtonian fluid down to diameters of 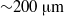${\sim }200~\mathrm{\mu} \mathrm{m} $. We investigate the flow of red blood cell (RBC) suspensions driven through small tubes (diameters 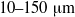$10\text{{\ndash}} 150~\mathrm{\mu} \mathrm{m} $) in the range marking the transition from arterioles and venules to the largest capillary vessels. The results of the simulations combined with previous simulations of uniform shear flow and experimental data show that for diameters less than 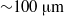${\sim }100~\mathrm{\mu} \mathrm{m} $ the suspension’s stress cannot be described as a continuum, even a heterogeneous one. We employ the dissipative particle dynamics (DPD) model, which has been successfully used to predict human blood bulk viscosity in homogeneous shear flow (Fedosov et al. Proc. Natl Acad. Sci. USA, vol. 108, 2011, pp. 11772–11777). In tube flow the cross-stream stress gradient induces an inhomogeneous distribution of RBCs featuring a centreline cell density peak, and a cell-free layer (CFL) next to the wall. For a neutrally buoyant suspension the imposed linear shear-stress distribution together with the differentiable velocity distribution allow the calculation of the local viscosity across the tube section. The viscosity across the section as a function of the strain rate is found to be essentially independent of tube size for the larger diameters and is determined by the local haematocrit (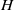$H$) and shear rate. Other RBC properties such as asphericity, deformation, and cell-flow orientation exhibit similar dependence for the larger tube diameters. As the tube size decreases below 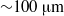${\sim }100~\mathrm{\mu} \mathrm{m} $ in diameter, the viscosity in the central region departs from the large-tube similarity function of the shear rate, since 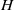$H$ increases significantly towards the centreline. The dependence of shear stress on tube size, in addition to the expected local shear rate and local haematocrit, implies that blood flow in small tubes cannot be described as a heterogeneous continuum. Based on the analysis of the DPD simulations and on available experimental results, we propose a simple velocity-slip model that can be used in conjunction with continuum-based simulations.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Capsule/cell dynamics Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 722 , 10 May 2013 , pp. 214 - 239
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alizadehrad, D., Imai, Y., Nakaaki, K., Ishikawa, T. & Yamaguchi, T. 2012 Quantification of red blood cell deformation at high-hematocrit bloodflow in microvessels. J. Biomech. 45, 2684–2689.Google Scholar
Barbee, J. H. & Cokelet, G. R. 1971 Prediction of blood flow in tubes with diameters as small as $29~\mathrm{\mu} $ . Microvasc. Res. 3, 17–21.CrossRefGoogle Scholar
Bugliarello, G. & Sevilla, J. 1970 Velocity distribution and other characteristics of steady and pulsatile blood flow in fine glass tubes. Biorheology 7, 85–107.CrossRefGoogle ScholarPubMed
Chien, S., Usami, S., Dellenback, R. J., Gregersen, M. I., Nanninga, L. B. & Guest, N. M. 1967 Blood viscosity: influence of erythrocyte aggregation. Science 157, 829–831.Google Scholar
Chien, S., Usami, S., Taylor, H. M., Lundberg, J. L. & Gregersen, M. I. 1966 Effects of hematocrit and plasma proteins on human blood rheology at low shear rates. J. Appl. Physiol. 21, 81–87.CrossRefGoogle ScholarPubMed
Cokelet, G. R. & Goldsmith, H. L. 1991 Decreased hydrodynamic resistance in the two-phase flow of blood through small vertical tubes at low flow rates. Circulat. Res. 68, 1–17.Google Scholar
Discher, D. E., Boal, D. H. & Boey, S. K. 1998 Simulations of the erythrocyte cytoskeleton at large deformation. II. Micropipette aspiration. Biophys. J. 75, 1584–1597.Google Scholar
Dupin, M. M., Halliday, I., Care, C. M., Alboul, L. & Munn, L. L. 2007 Modeling the flow of dense suspensions of deformable particles in three dimensions. Phys. Rev. E 75 (6), 066707.Google Scholar
Eckmann, D. M., Bowers, S., Stecker, M. & Cheung, A. T. 2000 Hematocrit, volume expander, temperature, and shear rate effects on blood viscosity. Anesthesia Analgesia 91, 539–545.Google Scholar
Espanol, P. & Warren, P. 1995 Statistical mechanics of dissipative particle dynamics. Europhys. Lett. 30, 191–196.Google Scholar
Evans, E. A. & Skalak, R. 1980 Mechanics and Thermodynamics of Biomembranes. CRC.Google Scholar
Fahraeus, R. 1929 The suspension stability of the blood. Physiol. Rev. 9, 241–274.CrossRefGoogle Scholar
Fahraeus, R. & Lindqvist, T. 1931 Viscosity of blood in narrow capillary tubes. Am. J. Phys. 96, 562–568.Google Scholar
Fan, X. J., Phan-Thien, N., Chen, S., Wu, X. H. & Ng, T. Y. 2006 Simulating flow of DNA suspension using dissipative particle dynamics. Phys. Fluids 18, 063102.CrossRefGoogle Scholar
Fedosov, D. A., Caswell, B. & Karniadakis, G. E. 2010a A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys. J. 98, 2215–2225.Google Scholar
Fedosov, D. A., Caswell, B. & Karniadakis, G. E. 2010b Steady shear rheometry of dissipative particle dynamics models of polymer fluids in reverse Poiseuille flow. J. Chem. Phys. 132, 144103.Google Scholar
Fedosov, D. A., Caswell, B. & Karniadakis, G. E. 2010c Systematic coarse-graining of spectrin-level red blood cell models. Comput. Meth. Appl. Mech. Engng 199, 1937–1948.Google Scholar
Fedosov, D. A., Caswell, B., Popel, A. S. & Karniadakis, G. E. 2010d Blood flow and cell-free layer in microvessels. Microcirculation 17, 615–628.CrossRefGoogle ScholarPubMed
Fedosov, D. A., Pan, W., Caswell, B., Gompper, G. & Karniadakis, G. E. 2011 Predicting human blood viscosity in silico. Proc. Natl Acad. Sci. USA 108, 11772–11777.Google Scholar
Freund, J. B. & Orescanin, M. M. 2011 Cellular flow in a small blood vessel. J. Fluid Mech. 671, 466–490.CrossRefGoogle Scholar
Gaehtgens, P., Dührssen, C. & Albrecht, K. H. 1980 Motion, deformation, and interaction of blood cells and plasma during flow through narrow capillary tubes. Blood Cells 6, 799–817.Google Scholar
Goldsmith, H. L., Cokelet, G. R. & Gaehtgens, P. 1989 Robin Fahraeus: evolution of his concepts in cardiovascular physiology. Am. J. Phys. 257, H1005–H1015.Google Scholar
Hoogerbrugge, P. J. & Koelman, J. M. V. A. 1992 Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 19, 155–160.CrossRefGoogle Scholar
Kim, S., Long, L. R., Popel, A. S., Intaglietta, M. & Johnson, P. C. 2007 Temporal and spatial variations of cell-free layer width in arterioles. Am. J. Phys. 293, H1526–H1535.Google ScholarPubMed
Lei, H., Caswell, B. & Karniadakis, G. E. 2010 Direct construction of mesoscopic models from microscopic simulations. Phys. Rev. E 81, 026704.Google Scholar
Maeda, N., Suzuki, Y., Tanaka, J. & Tateishi, N. 1996 Erythrocyte flow and elasticity of microvessels evaluated by marginal cell-free layer and flow resistance. Am. J. Phys. 271, H2454–H2461.Google Scholar
Mattice, W. L. & Suter, U. W. 1994 Conformational Theory of Large Molecules: The Rotational Isomeric State Model in Macromolecular Systems. Wiley.Google Scholar
McWhirter, L. J., Noguchi, H. & Gompper, G. 2009 Flow-induced clustering and alignment of vesicles and red blood cells in microcapillaries. Proc. Natl Acad. Sci. USA 106, 6039–6043.CrossRefGoogle ScholarPubMed
Merrill, E. W., Gilliland, E. R., Cokelet, G., Shin, H., Britten, A. & Wells, R. E. 1963 Rheology of human blood, near and at zero flow: effects of temperature and hematocrit level. Biophys. J. 3, 199–213.CrossRefGoogle ScholarPubMed
Merrill, E. W., Gilliland, E. R., Lee, T. S. & Salzman, E. W. 1966 Blood rheology: effect of fibrinogen deduced by addition. Circulat. Res. 18, 437–446.CrossRefGoogle ScholarPubMed
Moyers-Gonzalez, M. A. & Owens, R. G. 2010 Mathematical modelling of the cell-depleted peripheral layer in the steady flow of blood in a tube. Biorheology 47, 39–71.CrossRefGoogle ScholarPubMed
Popel, A. S. & Johnson, P. C. 2005 Microcirculation and hemorheology. Annu. Rev. Fluid Mech. 37, 43–69.Google Scholar
Pries, A. R., Ley, K., Claassen, M. & Gaehtgens, P. 1989 Red cell distribution at microvascular bifurcations. Microvasc. Res. 38, 81–101.Google Scholar
Pries, A. R., Neuhaus, D. & Gaehtgens, P. 1992 Blood viscosity in tube flow: dependence on diameter and hematocrit. Am. J. Phys. 263, H1770–H1778.Google Scholar
Reinke, W., Gaehtgens, P. & Johnson, P. C. 1987 Blood viscosity in small tubes: effect of shear rate, aggregation, and sedimentation. Am. J. Phys. 253, H540–H547.Google Scholar
Sharan, M. & Popel, A. S. 2001 A two-phase model for flow of blood in narrow tubes with increased effective viscosity near the wall. Biorheology 38, 415–428.Google Scholar
Skalak, R., Keller, S. R. & Secomb, T. W. 1981 Mechanics of blood flow. Trans. ASME: J. Biomech. Engng 103, 102–115.Google Scholar
Spalding, D. B. 1961 A simple formula for the ‘law of the wall’. Trans. ASME: J. Appl. Mech. 28, 455–458.Google Scholar