Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-13T23:38:15.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Bouncing on thin air: how squeeze forces in the air film during non-wetting droplet bouncing lead to momentum transfer and dissipation

Published online by Cambridge University Press:  13 July 2015

Jolet de Ruiter ,
Rudy Lagraauw ,
Frieder Mugele  and
Dirk van den Ende
Jolet de Ruiter
Affiliation:
Physics of Complex Fluids, MESA+ Institute for Nanotechnology, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Rudy Lagraauw
Affiliation:
Physics of Complex Fluids, MESA+ Institute for Nanotechnology, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Frieder Mugele
Affiliation:
Physics of Complex Fluids, MESA+ Institute for Nanotechnology, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Dirk van den Ende*
Affiliation:
Physics of Complex Fluids, MESA+ Institute for Nanotechnology, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
*
†Email address for correspondence: h.t.m.vandenende@utwente.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

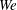Millimetre-sized droplets are able to bounce multiple times on flat solid substrates irrespective of their wettability, provided that a micrometre-thick air layer is sustained below the droplet, limiting $\mathit{We}$ to 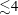${\lesssim}4$. We study the energy conversion during a bounce series by analysing the droplet motion and its shape (decomposed into eigenmodes). Internal modes are excited during the bounce, yet the viscous dissipation associated with the in-flight oscillations accounts for less than 20 % of the total energy loss. This suggests a significant contribution from the bouncing process itself, despite the continuous presence of a lubricating air film below the droplet. To study the role of this air film we visualize it using reflection interference microscopy. We quantify its thickness (typically a few micrometres) with sub-millisecond time resolution and 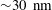${\sim}30~\text{nm}$ height resolution. Our measurements reveal strong asymmetry in the air film shape between the spreading and receding phases of the bouncing process. This asymmetry is crucial for effective momentum reversal of the droplet: lubrication theory shows that the dissipative force is repulsive throughout each bounce, even near lift-off, which leads to a high restitution coefficient. After multiple bounces the droplet eventually hovers on the air film, while continuously experiencing a lift force to sustain its weight. Only after a long time does the droplet finally wet the substrate. The observed bounce mechanism can be described with a single oscillation mode model that successfully captures the asymmetry of the air film evolution.

JFM classification

Drops and Bubbles: Drops Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 531 - 567
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Massachusetts Institute of Technology, Department of Mechanical Engineering, 77 Massachusetts Avenue, Cambridge, MA 02139, USA.

References

Antonini, C., Bernagozzi, I., Jung, S., Poulikakos, D. & Marengo, M. 2013 Water drops dancing on ice: how sublimation leads to drop rebound. Phys. Rev. Lett. 111, 014501.CrossRefGoogle ScholarPubMed
Arayanarakool, R., Shui, L. L., van den Berg, A. & Eijkel, J. C. T. 2011 A new method of UV-patternable hydrophobization of micro- and nanofluidic networks. Lab on a Chip 11, 4260–4266.Google Scholar
Becker, E., Hiller, W. & Kowalewski, T. 1991 Experimental and theoretical investigation of large-amplitude oscillations of liquid droplets. J. Fluid Mech. 231, 189–210.Google Scholar
Biance, A.-L., Chevy, F., Clanet, C., Lagubeau, G. & Quéré, D. 2006 On the elasticity of an inertial liquid shock. J. Fluid Mech. 554, 47–66.Google Scholar
Bird, J. C., Dhiman, R., Kwon, H.-M. & Varanasi, K. K. 2013 Reducing the contact time of a bouncing drop. Nature 503, 385–388.Google Scholar
Bouwhuis, W., van der Veen, R. C. A., Tran, T., Keij, D. L., Winkels, K. G., Peters, I. R., van der Meer, D., Sun, C., Snoeijer, J. H. & Lohse, D. 2012 Maximal air bubble entrainment at liquid-drop impact. Phys. Rev. Lett. 109, 264501.Google Scholar
Bouwhuis, W., Winkels, K. G., Peters, I. R., Brunet, P., van der Meer, D. & Snoeijer, J. H. 2013 Oscillating and star-shaped drops levitated by an airflow. Phys. Rev. E 88, 023017.Google Scholar
Caswell, T. A. 2014 Dynamics of the vapor layer below a Leidenfrost drop. Phys. Rev. E 90, 013014.Google Scholar
Chandra, S. & Avedisian, C. 1991 On the collision of a droplet with a solid surface. Proc. R. Soc. Lond. A 432, 13–41.Google Scholar
Chesters, A. K. 1991 The modeling of coalescence processes in fluid liquid dispersion: a review of current understanding. Chem. Engng Res. Des. 69, 259–270.Google Scholar
Chevy, F., Chepelianskii, A., Quéré, D. & Raphael, E. 2012 Liquid Hertz contact: softness of weakly deformed drops on non-wetting substrates. Europhys. Lett. 100, 54002.Google Scholar
Couder, Y., Fort, E., Gautier, C. H. & Boudaoud, A. 2005 From bouncing to floating: noncoalescence of drops on a fluid bath. Phys. Rev. Lett. 94, 177801.Google Scholar
Driscoll, M. M. & Nagel, S. R. 2011 Ultrafast interference imaging of air in splashing dynamics. Phys. Rev. Lett. 107, 154502.Google Scholar
Duchemin, L. & Josserand, C. 2011 Curvature singularity and film-skating during drop impact. Phys. Fluids 23, 091701.Google Scholar
Duchemin, L. & Josserand, C. 2012 Rarefied gas correction for the bubble entrapment singularity in drop impacts. C. R. Méc. 340, 797–803.Google Scholar
Gilet, T. & Bush, J. W. 2009 The fluid trampoline: droplets bouncing on a soap film. J. Fluid Mech. 625, 167–203.Google Scholar
Gilet, T., Terwagne, D., Vandewalle, N. & Dorbolo, S. 2008 Dynamics of a bouncing droplet onto a vertically vibrated interface. Phys. Rev. Lett. 100, 167802.Google Scholar
Hicks, P. D. & Purvis, R. 2010 Air cushioning and bubble entrapment in three-dimensional droplet impacts. J. Fluid Mech. 649, 135–163.CrossRefGoogle Scholar
Hicks, P. D. & Purvis, R. 2013 Liquid–solid impacts with compressible gas cushioning. J. Fluid Mech. 735, 120–149.Google Scholar
Klaseboer, E., Manica, R. & Chan, D. Y. 2014 Universal behavior of the initial stage of drop impact. Phys. Rev. Lett. 113, 194501.Google Scholar
Kolinski, J., Mahadevan, L. & Rubinstein, S. 2014a Drops can bounce from perfectly hydrophilic surfaces. Europhys. Lett. 108, 24001.Google Scholar
Kolinski, J. M., Mahadevan, L. & Rubinstein, S. M. 2014b Lift-off instability during the impact of a drop on a solid surface. Phys. Rev. Lett. 112, 134501.Google Scholar
Kolinski, J. M., Rubinstein, S. M., Mandre, S., Brenner, M. P., Weitz, D. A. & Mahadevan, L. 2012 Skating on a film of air: drops impacting on a surface. Phys. Rev. Lett. 108, 074503.Google Scholar
Liu, Y., Moevius, L., Xu, X., Qian, T., Yeomans, J. M. & Wang, Z. 2014 Pancake bouncing on superhydrophobic surfaces. Nat. Phys. 10, 515–519.CrossRefGoogle ScholarPubMed
Mahadevan, L. & Pomeau, Y. 1999 Rolling droplets. Phys. Fluids 11, 2449–2453.Google Scholar
Mandre, S. & Brenner, M. P. 2012 The mechanism of a splash on a dry solid surface. J. Fluid Mech. 690, 148–172.Google Scholar
Mandre, S., Mani, M. & Brenner, M. P. 2009 Precursors to splashing of liquid droplets on a solid surface. Phys. Rev. Lett. 102, 134502.Google Scholar
Mani, M., Mandre, S. & Brenner, M. P. 2010 Events before droplet splashing on a solid surface. J. Fluid Mech. 647, 163–185.Google Scholar
Miller, C. & Scriven, L. 1968 The oscillations of a fluid droplet immersed in another fluid. J. Fluid Mech. 32, 417–435.Google Scholar
Moláček, J. & Bush, J. W. 2012 A quasi-static model of drop impact. Phys. Fluids 24, 127103.Google Scholar
Oh, J. M., Ko, S. H. & Kang, K. H. 2008 Shape oscillation of a drop in AC electrowetting. Langmuir 24, 8379–8386.Google Scholar
Oh, J., Legendre, D. & Mugele, F. 2012 Shaken not stirred: on internal flow patterns in oscillating sessile drops. Europhys. Lett. 98, 34003.Google Scholar
Okumura, K., Chevy, F., Richard, D., Quéré, D. & Clanet, C. 2003 Water spring: a model for bouncing drops. Europhys. Lett. 62, 237–243.CrossRefGoogle Scholar
Richard, D., Clanet, C. & Quéré, D. 2002 Surface phenomena: contact time of a bouncing drop. Nature 417, 811.CrossRefGoogle Scholar
Richard, D. & Quéré, D. 2000 Bouncing water drops. Europhys. Lett. 50, 769–775.Google Scholar
de Ruiter, J., Lagraauw, R., van den Ende, D. & Mugele, F. 2015a Wettability-independent bouncing on flat surfaces mediated by thin air films. Nat. Phys. 11, 48–53.CrossRefGoogle Scholar
de Ruiter, J., Mugele, F. & van den Ende, D. 2015b Air cushioning in droplet impact. Part I. Dynamics of thin films studied by dual wavelength reflection interference microscopy. Phys. Fluids 27, 012104.Google Scholar
de Ruiter, J., Oh, J. M., van den Ende, D. & Mugele, F. 2012 Dynamics of collapse of air films in drop impact. Phys. Rev. Lett. 108, 074505.Google Scholar
de Ruiter, J., van den Ende, D. & Mugele, F. 2015c Air cushioning in droplet impact. Part II. Experimental characterization of the air film evolution. Phys. Fluids 27, 012105.Google Scholar
Smith, F. T., Li, L. & Wu, G. X. 2003 Air cushioning with a lubrication/inviscid balance. J. Fluid Mech. 482, 291–318.Google Scholar
Terwagne, D., Ludewig, F., Vandewalle, N. & Dorbolo, S. 2013 The role of the droplet deformations in the bouncing droplet dynamics. Phys. Fluids 25, 122101.Google Scholar
Terwagne, D., Vandewalle, N. & Dorbolo, S. 2007 Lifetime of a bouncing droplet. Phys. Rev. E 76, 056311.Google ScholarPubMed
Tran, T., Staat, H. J. J., Prosperetti, A., Sun, C. & Lohse, D. 2012 Drop impact on superheated surfaces. Phys. Rev. Lett. 108, 036101.Google Scholar
Tsougeni, K., Vourdas, N., Tserepi, A., Gogolides, E. & Cardinaud, C. 2009 Mechanisms of oxygen plasma nanotexturing of organic polymer surfaces: from stable super hydrophilic to super hydrophobic surfaces. Langmuir 25, 11748–11759.Google Scholar
van der Veen, R. C., Tran, T., Lohse, D. & Sun, C. 2012 Direct measurements of air layer profiles under impacting droplets using high-speed color interferometry. Phys. Rev. E 85, 026315.Google Scholar
Yarin, A. 2006 Drop impact dynamics: splashing, spreading, receding, bouncing …. Annu. Rev. Fluid Mech. 38, 159–192.Google Scholar