Article contents
Boundary layer fluctuations in turbulent Rayleigh–Bénard convection
Published online by Cambridge University Press: 13 February 2018
Abstract
We report a combined experimental and numerical study of the effect of boundary layer (BL) fluctuations on the scaling properties of the mean temperature profile 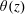 $\unicode[STIX]{x1D703}(z)$ and temperature variance profile
$\unicode[STIX]{x1D703}(z)$ and temperature variance profile 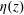 $\unicode[STIX]{x1D702}(z)$ in turbulent Rayleigh–Bénard convection in a thin disk cell and an upright cylinder of aspect ratio unity. Two scaling regions are found with increasing distance
$\unicode[STIX]{x1D702}(z)$ in turbulent Rayleigh–Bénard convection in a thin disk cell and an upright cylinder of aspect ratio unity. Two scaling regions are found with increasing distance  $z$ away from the bottom conducting plate. In the BL region, the measured
$z$ away from the bottom conducting plate. In the BL region, the measured 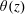 $\unicode[STIX]{x1D703}(z)$ and
$\unicode[STIX]{x1D703}(z)$ and 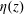 $\unicode[STIX]{x1D702}(z)$ are found to have the scaling forms
$\unicode[STIX]{x1D702}(z)$ are found to have the scaling forms 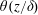 $\unicode[STIX]{x1D703}(z/\unicode[STIX]{x1D6FF})$ and
$\unicode[STIX]{x1D703}(z/\unicode[STIX]{x1D6FF})$ and 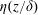 $\unicode[STIX]{x1D702}(z/\unicode[STIX]{x1D6FF})$ , respectively, with varying thermal BL thickness
$\unicode[STIX]{x1D702}(z/\unicode[STIX]{x1D6FF})$ , respectively, with varying thermal BL thickness 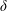 $\unicode[STIX]{x1D6FF}$ . The functional forms of the measured
$\unicode[STIX]{x1D6FF}$ . The functional forms of the measured 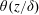 $\unicode[STIX]{x1D703}(z/\unicode[STIX]{x1D6FF})$ and
$\unicode[STIX]{x1D703}(z/\unicode[STIX]{x1D6FF})$ and  $\unicode[STIX]{x1D702}(z/\unicode[STIX]{x1D6FF})$ in the two convection cells agree well with the recently derived BL equations by Shishkina et al. (Phys. Rev. Lett., vol. 114, 2015, 114302) and by Wang et al. (Phys. Rev. Fluids, vol. 1, 2016, 082301). In the mixing zone outside the BL region, the measured
$\unicode[STIX]{x1D702}(z/\unicode[STIX]{x1D6FF})$ in the two convection cells agree well with the recently derived BL equations by Shishkina et al. (Phys. Rev. Lett., vol. 114, 2015, 114302) and by Wang et al. (Phys. Rev. Fluids, vol. 1, 2016, 082301). In the mixing zone outside the BL region, the measured 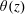 $\unicode[STIX]{x1D703}(z)$ remains approximately constant, whereas the measured
$\unicode[STIX]{x1D703}(z)$ remains approximately constant, whereas the measured 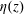 $\unicode[STIX]{x1D702}(z)$ is found to scale with the cell height
$\unicode[STIX]{x1D702}(z)$ is found to scale with the cell height  $H$ in the two convection cells and follows a power law,
$H$ in the two convection cells and follows a power law, 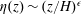 $\unicode[STIX]{x1D702}(z)\sim (z/H)^{\unicode[STIX]{x1D716}}$ , with the obtained values of
$\unicode[STIX]{x1D702}(z)\sim (z/H)^{\unicode[STIX]{x1D716}}$ , with the obtained values of  $\unicode[STIX]{x1D716}$ being close to
$\unicode[STIX]{x1D716}$ being close to 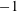 $-1$ . Based on the experimental and numerical findings, we derive a new equation for
$-1$ . Based on the experimental and numerical findings, we derive a new equation for 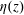 $\unicode[STIX]{x1D702}(z)$ in the mixing zone, which has a power-law solution in good agreement with the experimental and numerical results. Our work demonstrates that the effect of BL fluctuations can be adequately described by the velocity–temperature correlation functions and the new BL equations capture the essential physics.
$\unicode[STIX]{x1D702}(z)$ in the mixing zone, which has a power-law solution in good agreement with the experimental and numerical results. Our work demonstrates that the effect of BL fluctuations can be adequately described by the velocity–temperature correlation functions and the new BL equations capture the essential physics.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 25
- Cited by

