Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-30T21:56:00.191Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary layers in Helmholtz flows

Published online by Cambridge University Press:  11 November 2019

Madeleine Rose Moore Open the ORCID record for Madeleine Rose Moore [Opens in a new window] ,
R. Cimpeanu Open the ORCID record for R. Cimpeanu [Opens in a new window] ,
H. Ockendon ,
J. R. Ockendon  and
J. M. Oliver
Madeleine Rose Moore*
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, OxfordOX2 6GG, UK
R. Cimpeanu
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, OxfordOX2 6GG, UK Mathematical Institute, Zeeman Building, University of Warwick, CoventryCV4 7AL, UK
H. Ockendon
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, OxfordOX2 6GG, UK
J. R. Ockendon
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, OxfordOX2 6GG, UK
J. M. Oliver
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, OxfordOX2 6GG, UK
*
†Email address for correspondence: moorem@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

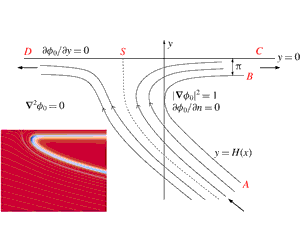
Recent comparisons between classical Wagner theory for the impact of two liquid droplets and direct numerical simulations in Cimpeanu & Moore (J. Fluid Mech., vol. 856, 2018, pp. 764–796) show that, in some regimes, the inviscid theory over-predicts the thickness of the root of the splash jet that forms in the impact, while also struggling to predict the angle at which the jet is emitted. The effect of capillary and viscous perturbations to Helmholtz flows was investigated in a previous study, see Moore et al. (J. Fluid Mech., vol. 742, 2014, R1). However, the paper in question ignored a term in the second-order perturbation analysis, which needs to be included in order to predict the displacement of the inviscid free boundary to lowest order. In this paper, we derive a singular integro-differential equation for the free-surface perturbations caused by viscosity in Helmholtz flows and discuss its application both in the context of Wagner theory and more generally. In particular, viscosity can induce non-monotonic behaviour in the free boundary profiles near points of maximum curvature.

JFM classification

Boundary Layers: Boundary Layers Interfacial Flows (free surface): Interfacial Flows (free surface)
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 882 , 10 January 2020 , A19
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Article last updated 07 March 2023

References

Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Cimpeanu, R. & Moore, M. R. 2018 Early-time jet formation in liquid–liquid impact problems: theory and simulations. J. Fluid Mech. 856, 764–796.Google Scholar
Hooper, A. P. & Boyd, W. G. C. 1983 Shear-flow instability at the interface between two viscous fluids. J. Fluid Mech. 128, 507–528.Google Scholar
Howison, S. D., Ockendon, J. R. & Wilson, S. K. 1991 Incompressible water-entry problems at small deadrise angles. J. Fluid Mech. 222, 215–230.Google Scholar
Milne-Thomson, L. M. 1996 Theoretical Hydrodynamics. Dover.Google Scholar
Moore, M. R., Ockendon, H., Ockendon, J. R. & Oliver, J. M. 2014 Capillary and viscous perturbations to Helmholtz flows. J. Fluid Mech. 742, R1.Google Scholar
Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 190, 572–600.Google Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228, 5838–5866.Google Scholar
Purvis, R. & Smith, F. T. 2005 Droplet impact on water layers: post-impact analysis and computations. Phil. Trans. R. Soc. Lond. A 363, 1209–1221.Google Scholar
Wagner, H. 1932 Über Stoß- und Gleitvorgänge an der Oberfläche von Flüssigkeiten. Z. Angew. Math. Mech. 12, 193–215.Google Scholar