Hostname: page-component-7dd5485656-kp629 Total loading time: 0 Render date: 2025-10-31T10:17:34.392Z Has data issue: false hasContentIssue false
  • English
  • Français

Breaking electrolyte symmetry in induced-charge electro-osmosis

Published online by Cambridge University Press:  27 October 2020

Aditya S. Khair Open the ORCID record for Aditya S. Khair [Opens in a new window]  and
Bhavya Balu
Aditya S. Khair*
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Bhavya Balu
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
*
†Email address for correspondence: akhair@andrew.cmu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

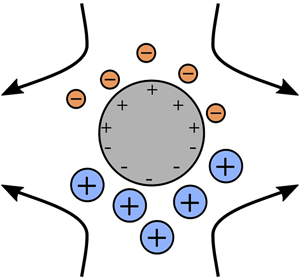
Induced-charge electro-osmotic (ICEO) flow caused by an alternating electric field applied around an infinitely long, ideally polarizable, uncharged circular cylinder in a binary electrolyte with unequal cation and anion diffusion coefficients is analysed. The thin-Debye-layer and weak-field approximations are invoked to compute the time-averaged, or rectified, quadrupolar ICEO flow around the cylinder. The inequality of ionic diffusion coefficients leads to transient ion concentration gradients, or concentration polarization, in the electroneutral bulk electrolyte outside the Debye layer. Consequently, the electric potential in the bulk is non-harmonic. Further, the concentration polarization alters the electro-osmotic slip at the surface of the cylinder and generates body forces in the bulk, both of which affect the rectified ICEO flow. Predictions for the strength of the rectified flow for varying ratio of ionic diffusion coefficients are in reasonable agreement with available experimental data. Our work highlights that an inequality in ionic diffusion coefficients – which all electrolytes possess to some extent – is an important factor in modelling ICEO flows.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 905 , 25 December 2020 , A20
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Canpolat, C., Qian, S. & Beskok, A. 2013 Micro-PIV measurements of induced-charge electro-osmosis around a metal rod. Microfluid Nanofluid 14, 153–162.CrossRefGoogle Scholar
Chew, W. C & Sen, P. N. 1982 Dielectric enhancement due to electrochemical double layer: thin double layer approximation. J. Chem. Phys. 77, 4683–4693.CrossRefGoogle Scholar
DeLacey, E. H. B. & White, L. R. 1982 The polarization impedance of an ideally polarizable plane electrode. J. Chem. Soc. Faraday Trans. 78, 457–479.CrossRefGoogle Scholar
Dukhin, S. S. 1993 Non-equilibrium electric surface phenomena. Adv. Colloid Interface Sci. 44, 1–134.CrossRefGoogle Scholar
Feng, H., Huang, Y., Wong, T. N. & Duan, F. 2018 Electrolyte effect in induced charge electroosmosis. Soft Matt. 13, 4864–4870.CrossRefGoogle Scholar
Gamayunov, N. I., Murtsovkin, V. A. & Dukhin, A. S. 1986 Pair interactions of particles in electric field. 1. Features of hydrodynamic interaction of polarized particles. Colloid J. USSR 48, 233–239.Google Scholar
Gamayunov, N. I., Mantrov, G. I. & Murtsovkin, V. A. 1992 Study of flows induced in the vicinity of conducting particles by an external electric-field. Colloid J. USSR 54, 20–23.Google Scholar
Gangwal, S., Cayre, O. J., Bazant, M. Z. & Velev, O. D. 2008 Induced-charge electrophoresis of metallodielectric particles. Phys. Rev. Lett. 100, 058302.CrossRefGoogle ScholarPubMed
García-Sánchez, P., Ramos, A., González, A., Green, N. G. & Morgan, H. 2009 Flow reversal in traveling-wave electrokinetics: an analysis of forces due to ionic concentration gradients. Langmuir 25, 4988–4997.CrossRefGoogle ScholarPubMed
García-Sánchez, P., Loucaides, N. G. & Ramos, A. 2017 Pumping of electrolytes by electrical forces induced on the diffusion layer: a weakly nonlinear analysis. Phys. Rev. E 95, 022802.CrossRefGoogle ScholarPubMed
González, A., Ramos, A., García-Sánchez, P. & Castellanos, A. 2010 Effect of the combined action of Faradaic currents and mobility differences in ac electro-osmosis. Phys. Rev. E 81, 016320.CrossRefGoogle ScholarPubMed
Hashemi Amrei, S. M. H., Bukosky, S. C., Rader, S. P., Ristenpart, W. D. & Miller, G. H. 2018 Oscillating electric fields in liquids create a long-range steady field. Phys. Rev. Lett. 121, 185504.CrossRefGoogle ScholarPubMed
Hashemi Amrei, S. M. H., Miller, G. H. & Ristenpart, W. D. 2020 Asymmetric rectified electric fields generate flows that can dominate induced-charge electrokinetics. Phys. Rev. Fluids 5, 013702.CrossRefGoogle Scholar
Khair, A. S. & Squires, T. M. 2008 Fundamental aspects of concentration polarization arising from nonuniform electrokinetic transport. Phys. Fluids 20, 087102.CrossRefGoogle Scholar
Levitan, J. A., Devasenathipathy, S., Studer, V., Ben, Y., Thorsen, T., Squires, T. M. & Bazant, M. Z. 2005 Experimental observation of induced-charge electro-osmosis around a metal wire in a microchannel. Colloids Surf. A 267, 122–132.CrossRefGoogle Scholar
Olesen, L. H., Bazant, M. Z. & Bruus, H. 2010 Strongly nonlinear dynamics of electrolytes in large ac voltages. Phys. Rev. E 82, 011501.CrossRefGoogle Scholar
Paustian, J. S., Pascall, A., Wilson, N. M & Squires, T. M. 2014 Induced charge electroosmosis micropumps using arrays of Janus micropillars. Lab on a Chip 14, 3300–3312.CrossRefGoogle ScholarPubMed
Peng, C., Lazo, I., Shiyanovskii, S. V. & Lavrentovich, O. D. 2014 Induced-charge electro-osmosis around metal and Janus spheres in water: patterns of flow and breaking symmetries. Phys. Rev. E 90, 051002.CrossRefGoogle ScholarPubMed
Ramos, A., Morgan, H., Green, N. G. & Castellanos, A. 1999 AC electric-field-induced fluid flow in microelectrodes. J. Colloid Interface Sci. 217, 420–422.CrossRefGoogle ScholarPubMed
Saville, D. A. 1977 Electrokinetic effects with small particles. Annu. Rev. Fluid Mech. 9, 321–337.CrossRefGoogle Scholar
Schnitzer, O. & Yariv, E. 2012 Induced-charge electro-osmosis beyond weak fields. Phys. Rev. E 86, 061506.CrossRefGoogle ScholarPubMed
Shilov, V. N. & Dukhin, S. S. 1970 Theory of polarization of the diffuse part of a thin double layer at a spherical particle in an alternating electric field. Colloid J. USSR 32, 117–123.Google Scholar
Squires, T. M. & Bazant, M. Z. 2004 a Induced-charge electrokinetic phenomena: theory and microfluidic applications. Phys. Rev. Lett. 92, 066101.Google Scholar
Squires, T. M. & Bazant, M. Z. 2004 b Induced-charge electro-osmosis. J. Fluid Mech. 509, 217–252.CrossRefGoogle Scholar
Squires, T. M. & Bazant, M. Z. 2006 Breaking symmetries in induced-charge electro-osmosis and electrophoresis. J. Fluid Mech. 560, 65–101.CrossRefGoogle Scholar
Squires, T. M. & Bazant, M. Z. 2010 Induced-charge electrokinetic phenomena. Curr. Opin. Colloid Interface Sci. 15, 203–213.Google Scholar
Vanýsek, P. 2012 Ionic conductivity and diffusion at infinite dilution. In CRC Handbook of Chemistry and Physics, 97th edn (ed. Haynes, W. H.). CRC Press.Google Scholar