Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T07:14:44.000Z Has data issue: false hasContentIssue false
  • English
  • Français

Carbon dioxide dissolution in structural and stratigraphic traps

Published online by Cambridge University Press:  06 November 2013

M. L. Szulczewski ,
M. A. Hesse  and
R. Juanes
M. L. Szulczewski
Affiliation:
Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
M. A. Hesse
Affiliation:
Department of Geological Sciences and Institute for Computational Engineering and Sciences, University of Texas at Austin, Austin, TX 78712, USA
R. Juanes*
Affiliation:
Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: juanes@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The geologic sequestration of carbon dioxide ( CO2) in structural and stratigraphic traps is a viable option to reduce anthropogenic emissions. While dissolution of the CO2 stored in these traps reduces the long-term leakage risk, the dissolution process remains poorly understood in systems that reflect the appropriate subsurface geometry. Here, we study dissolution in a porous layer that exhibits a feature relevant for CO2 storage in structural and stratigraphic traps: a finite CO2 source along the top boundary that extends only part way into the layer. This feature represents the finite extent of the interface between free-phase CO2 pooled in a trap and the underlying brine. Using theory and simulations, we describe the dissolution mechanisms in this system for a wide range of times and Rayleigh numbers, and classify the behaviour into seven regimes. For each regime, we quantify the dissolution flux numerically and model it analytically, with the goal of providing simple expressions to estimate the dissolution rate in real systems. We find that, at late times, the dissolution flux decreases relative to early times as the flow of unsaturated water to the CO2 source becomes constrained by a lateral exchange flow though the reservoir. 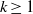Application of the models to several representative reservoirs indicates that dissolution is strongly affected by the reservoir properties; however, we find that reservoirs with high permeabilities ($k\geq 1$ Darcy) that are tens of metres thick and several kilometres wide could potentially dissolve hundreds of megatons of CO2 in tens of years.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 736 , 10 December 2013 , pp. 287 - 315
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ascher, U. M., Ruuth, S. J. & Spiteri, R. J. 1997 Implicit–explicit Runge–Kutta methods for time-dependent partial differential equations. Appl. Numer. Maths 25, 151–167.Google Scholar
Backhaus, S., Turitsyn, K. & Ecke, R. E. 2011 Convective instability and mass transport of diffusion layers in a Hele-Shaw geometry. Phys. Rev. Lett. 106, 104501.Google Scholar
Bear, J. 1972 Dynamics of Fluids in Porous Media. Elsevier, reprinted with corrections by Dover, 1988.Google Scholar
Benson, S. M. & Cole, D. R. 2008 ${\mathrm{CO} }_{2} $ sequestration in deep sedimentary formations. Elements 4 (5), 325–331.CrossRefGoogle Scholar
Cheng, P. & Chang, I. 1976 Buoyancy induced flows in a saturated porous medium adjacent to impermeable horizontal surfaces. Intl J. Heat Mass Transfer 19, 1267–1272.Google Scholar
Chiaramonte, L., Zoback, M. D., Friedmann, J. & Stamp, V. 2008 Seal integrity and feasibility of ${\mathrm{CO} }_{2} $ sequestration in the Teapot Dome EOR pilot: geomechanical site characterization. Environ. Geol. 54 (8), 1667–1675.CrossRefGoogle Scholar
Crank, J. 1980 The Mathematics of Diffusion. Oxford University Press.Google Scholar
De Josselin De Jong, G. 1981 The simultaneous flow of fresh and salt water in aquifers of large horizontal extension determined by shear flow and vortex theory. Proc. Euromech. 143, 75–82.Google Scholar
Elder, J. W. 1967 Transient convection in a porous medium. J. Fluid Mech. 27 (3), 609–623.Google Scholar
Ennis-King, J., Preston, I. & Paterson, L. 2005 Onset of convection in anisotropic porous media subject to a rapid change in boundary conditions. Phys. Fluids 17, 084107.Google Scholar
Grasso, J. R. 1992 Mechanics of seismic instabilities induced by the recovery of hydrocarbons. Pure Appl. Geophys. 139 (3/4), 507–534.CrossRefGoogle Scholar
Gunter, W. D., Bachu, S. & Benson, S. 2004 The role of hydrogeological and geochemical trapping in sedimentary basins for secure geological storage of carbon dioxide. In Geological Storage of Carbon Dioxide (ed. Baines, S. J. & Worden, R. H.), Special Publications, vol. 233, pp. 129–145. Geological Society.Google Scholar
Hassanzadeh, H., Pooladi-Darvish, M. & Keith, D. W. 2007 Scaling behaviour of convective mixing, with application to geological storage of ${\mathrm{CO} }_{2} $ . AIChE J. 53 (5), 1121–1131.CrossRefGoogle Scholar
Hesse, M. A. 2008 Mathematical modelling and multiscale simulation for ${\mathrm{CO} }_{2} $ storage in saline aquifers. PhD thesis, Stanford University, Department of Energy Resources Engineering.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.Google Scholar
Hidalgo, J. J., Fe, J., Cueto-Felgueroso, L. & Juanes, R. 2012 Scaling of convective mixing in porous media. Phys. Rev. Lett. 109, 264503.Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.Google Scholar
IPCC, 2005 Special Report on Carbon Dioxide Capture and Storage (ed. B. Metz et al.) Cambridge University Press.Google Scholar
Kneafsey, T. J. & Pruess, K. 2010 Laboratory flow experiments for visualizing carbon dioxide-induced, density-driven brine convection. Transp. Porous Med. 82, 123–139.Google Scholar
Lackner, K. S. 2003 A guide to ${\mathrm{CO} }_{2} $ sequestration. Science 300 (5626), 1677–1678.Google Scholar
Lambert, J. D. 1991 Numerical Methods for Ordinary Differential Systems: The Initial Value Problem. Wiley.Google Scholar
LeVeque, R. J. 2002 Finite Volume Methods for Hyperbolic Problems. Cambridge University Press.CrossRefGoogle Scholar
MacMinn, C. W. & Juanes, R. 2013 Buoyant currents arrested by convective dissolution. Geophys. Res. Lett. 40 (10), 2017–2022.Google Scholar
Mathias, S. A., Hardisty, P. E., Trudell, M. R. & Zimmerman, R. W. 2009 Screening and selection of sites for ${\mathrm{CO} }_{2} $ sequestration based on pressure buildup. Intl J. Greenh. Gas Control 3, 577–585.Google Scholar
Michael, K., Golab, A., Shulakova, V., Ennis-King, J., Allinson, G., Sharma, S. & Aiken, T. 2010 Geological storage of ${\mathrm{CO} }_{2} $ in saline aquifers: a review of the experience from existing storage operations. Intl J. Greenh. Gas Control 4, 659–667.Google Scholar
Mito, S., Xue, Z. & Sato, T. 2013 Effect of formation water composition on predicting ${\mathrm{CO} }_{2} $ behaviour: a case study at the Nagaoka post-injection monitoring site. Appl. Geochem. 30, 33–40.Google Scholar
Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, H. A. & Huppert, H. E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, L22404.CrossRefGoogle Scholar
Nield, D. A. & Bejan, A. 2013 Convection in Porous Media, 4th edn. Springer.Google Scholar
Orr, F. M. Jr. 2009 Onshore geologic storage of ${\mathrm{CO} }_{2} $ . Science 325, 1656–1658.CrossRefGoogle Scholar
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewskia, M. J. & Zhang, K. 2010 High-resolution simulation and characterization of density-driven flow in ${\mathrm{CO} }_{2} $ storage in saline aquifers. Adv. Water Resour. 33 (4), 443–455.Google Scholar
Rapaka, S., Chen, S., Pawar, R., Stauffer, P. & Zhang, D. 2008 Non-modal growth of perturbations in density-driven convection in porous media. J. Fluid Mech. 609, 285–303.CrossRefGoogle Scholar
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M. Jr. 2006 Onset of convection in a gravitationally unstable, diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.CrossRefGoogle Scholar
Rutqvist, J. & Tsang, C. 2002 A study of caprock hydromechanical changes associated with ${\mathrm{CO} }_{2} $ -injection into a brine formation. Environ. Geol. 42, 296–305.Google Scholar
Schrag, D. P. 2007 Preparing to capture carbon. Science 315, 812–813.Google Scholar
Slim, A. C., Bandi, M. M., Miller, J. C. & Mahadevan, L. 2013 Dissolution-driven convection in a Hele-Shaw cell. Phys. Fluids 25, 024101.Google Scholar
Slim, A. C. & Ramakrishnan, T. S. 2010 Onset and cessation of time-dependent, dissolution-driven convection in porous media. Phys. Fluids 22, 124103.CrossRefGoogle Scholar
Strang, G. 2007 Computational Science and Engineering. Wellesley–Cambridge Press.Google Scholar
Szulczewski, M. L. & Juanes, R. 2013 The evolution of miscible gravity currents in horizontal porous layers. J. Fluid Mech. 719, 82–96.CrossRefGoogle Scholar
Szulczewski, M. L., MacMinn, C. W., Herzog, H. J. & Juanes, R. 2012 Lifetime of carbon capture and storage as a climate-change mitigation technology. Proc. Natl Acad. Sci. USA 109 (14), 5185–5189.CrossRefGoogle ScholarPubMed
Underschultz, J., Boreham, C., Dance, T., Stalker, L., Freifeld, B., Kirste, D. & Ennis-King, J. 2011 ${\mathrm{CO} }_{2} $ storage in a depleted gas field: an overview of the CO2CRC Otway Project and initial results. Intl J. Greenh. Gas Control 5, 922–932.CrossRefGoogle Scholar
US Energy Information Administration, US Department of Energy 2009 Emissions of greenhouse gases in the United States 2008. Report no. DOE/EIA-0573(2008). http://www.eia.gov/oiaf/1605/ggrpt/pdf/0573(2008).pdf.Google Scholar
Wooding, R. A., Tyler, S. W. & White, I. 1997a Convection in groundwater below an evaporating salt lake. Part 1. Onset of instability. Water Resour. Res. 33 (6), 1199–1217.CrossRefGoogle Scholar
Wooding, R. A., Tyler, S. W. & White, I. 1997b Convection in groundwater below an evaporating salt lake. Part 2. Evolution of fingers or plumes. Water Resour. Res. 33 (6), 1219–1228.Google Scholar
Xu, X., Chen, S. & Zhang, D. 2006 Convective stability analysis of the long-term storage of carbon dioxide in deep saline aquifers. Adv. Water Resour. 29, 397–407.CrossRefGoogle Scholar