Article contents
Characteristics of the turbulent non-turbulent interface in a spatially evolving turbulent mixing layer
Published online by Cambridge University Press: 28 April 2020
Abstract
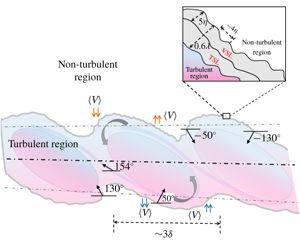
The highly convoluted interface separating the turbulent and non-turbulent regions in a turbulent mixing layer is experimentally investigated using the particle image velocimetry (PIV) technique. The mixing layer was generated using a fine screen/mesh in one half of the test section of a low-speed wind tunnel. The PIV data, which were acquired with high spatial resolution in the self-similar regime of the flow, allow us to identify the turbulent/non-turbulent interface (TNTI) using a suitable threshold value of the absolute spanwise vorticity,  $|\unicode[STIX]{x1D714}_{z}|$. The threshold values for the top and bottom interfaces of the mixing layer are found to be different, and the probability density function (PDF) of the interface position for both the interfaces is found to follow the Gaussian distribution. Interestingly, the PDF of the interface orientation reveals two clear peaks, and this is attributed to the sustained large-scale motions in a mixing layer, compared to the other free-shear flows, as is also substantiated by further analyses such as the linear stochastic estimation and the conditional analysis of the transverse velocity profile. The linear stochastic analysis also shows the presence of large vorticity structures of the order of the Taylor microscale at the mean TNTI location in a mixing layer. Furthermore, the present work reveals that, using the spanwise component of vorticity alone, we can experimentally identify and estimate the thickness of the viscous superlayer from the conditional profiles of the diffusion term and the correlation coefficient of the dissipation and the diffusion terms in the enstropy transport equation. The present value of the viscous superlayer thickness of
$|\unicode[STIX]{x1D714}_{z}|$. The threshold values for the top and bottom interfaces of the mixing layer are found to be different, and the probability density function (PDF) of the interface position for both the interfaces is found to follow the Gaussian distribution. Interestingly, the PDF of the interface orientation reveals two clear peaks, and this is attributed to the sustained large-scale motions in a mixing layer, compared to the other free-shear flows, as is also substantiated by further analyses such as the linear stochastic estimation and the conditional analysis of the transverse velocity profile. The linear stochastic analysis also shows the presence of large vorticity structures of the order of the Taylor microscale at the mean TNTI location in a mixing layer. Furthermore, the present work reveals that, using the spanwise component of vorticity alone, we can experimentally identify and estimate the thickness of the viscous superlayer from the conditional profiles of the diffusion term and the correlation coefficient of the dissipation and the diffusion terms in the enstropy transport equation. The present value of the viscous superlayer thickness of  $5\unicode[STIX]{x1D702}$–
$5\unicode[STIX]{x1D702}$– $6\unicode[STIX]{x1D702}$ (where
$6\unicode[STIX]{x1D702}$ (where  $\unicode[STIX]{x1D702}$ is the Kolmogorov length scale) compares well with the values reported in the literature for other shear flows. Although both the interfaces are found to behave like a fractal with a dimension of 1.3 in two dimensions, one can find dominant length scales of the order of the thickness of the viscous superlayer, the thickness of the TNTI and the width of the mixing layer from the pre-multiplied power spectra of the autocorrelation functions of the interface curvature, the normal velocity and the interface position, along the TNTI, respectively. In addition, we find that the TNTI characteristics do not show significant dependence on the velocity ratios and
$\unicode[STIX]{x1D702}$ is the Kolmogorov length scale) compares well with the values reported in the literature for other shear flows. Although both the interfaces are found to behave like a fractal with a dimension of 1.3 in two dimensions, one can find dominant length scales of the order of the thickness of the viscous superlayer, the thickness of the TNTI and the width of the mixing layer from the pre-multiplied power spectra of the autocorrelation functions of the interface curvature, the normal velocity and the interface position, along the TNTI, respectively. In addition, we find that the TNTI characteristics do not show significant dependence on the velocity ratios and  $Re_{\unicode[STIX]{x1D706}}$ considered in the present study. Furthermore, the conditional transverse velocity profiles indicate that the entrainment characteristics for the upper and lower TNTIs may be asymmetric in nature.
$Re_{\unicode[STIX]{x1D706}}$ considered in the present study. Furthermore, the conditional transverse velocity profiles indicate that the entrainment characteristics for the upper and lower TNTIs may be asymmetric in nature.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 29
- Cited by


