1. Introduction
Fundamental research on microorganisms’ swimming in general, and ciliary propulsion in particular, is of great practical importance. It has led to the development of microrobots (Nelson, Kaliakatsos & Abbott Reference Nelson, Kaliakatsos and Abbott2010; Wu et al. Reference Wu, Chen, Mukasa, Pak and Gao2020) that are employed in a wide range of biological and biomedical applications (Wang et al. Reference Wang2022) such as drug delivery systems (Gao et al. Reference Gao, Kagan, Pak, Clawson, Campuzano, Chuluun-Erdene, Fullerton, Zhang, Lauga and Wang2012; Li et al. Reference Li, de Avila, Gao, Zhang and Wang2017; Tsang et al. Reference Tsang, Demir, Ding and Pak2020; Wu et al. Reference Wu, Chen, Mukasa, Pak and Gao2020; Zhang et al. Reference Zhang, Li, Gao, Fan, Pang, Li, Wu, Xie and He2021). Lighthill's seminal work on ciliary propulsion in a Newtonian fluid (Lighthill Reference Lighthill1952) spearheaded many modern studies on the swimming of ciliated microorganisms. The pioneering study remains the reference to assess the performance metrics of ciliated microorganisms in a variety of environments including heterogeneous media (Leshansky Reference Leshansky2009; Nganguia & Pak Reference Nganguia and Pak2018) and complex fluids (Pak et al. Reference Pak, Zhu, Brandt and Lauga2012; Datt et al. Reference Datt, Zhu, Elfring and Pak2015; Pietrzyk et al. Reference Pietrzyk, Nganguia, Datt, Zhu, Elfring and Pak2019). A common feature between Lighthill and the investigations that followed is the assumption of a background uniform flow. However, many biological systems live in dynamic fluid environments that are subject to non-uniform flows such as small pathogens in blood vessels (Uppaluri et al. Reference Uppaluri, Heddergott, Stellamanns, Herminghaus, Zottl, Stark, Engstler and Pfohl2012), spermatozoa swimming through cervical mucus and vaginal fluid (Rutllant, Lopez-Bejar & Lopez-Gatius Reference Rutllant, Lopez-Bejar and Lopez-Gatius2005; Riffell & Zimmer Reference Riffell and Zimmer2007; Zimmer & Riffell Reference Zimmer and Riffell2011; Denissenko et al. Reference Denissenko, Kantsler, Smith and Kirkman-Brown2012), among others.
Focusing specifically on Poiseuille flows ubiquitous in the biological microcirculation, experiments dating back to the 1960s have explored its effect on the dynamics of a suspension of particles (Goldsmith & Mason Reference Goldsmith and Mason1961; Segré & Silberberg Reference Segré and Silberberg1961). Later, Kessler investigated the influence of Poiseuille flows on the directed locomotion of algal cells (Kessler Reference Kessler1985) whereas, much more recently, other investigators have reported Poiseuille flows’ effects on the dynamics, orientations and trajectories of biological microorganisms (Zottl & Stark Reference Zottl and Stark2012; Choudhary et al. Reference Choudhary, Paul, Ruhle and Stark2022; Omori et al. Reference Omori, Kikuchi, Schmitz, Pavlovic, Chuang and Ishikawa2022; Walker et al. Reference Walker, Ishimoto, Moreau, Gaffney and Dalwadi2022), artificial microswimmers (Acemoglu & Yesilyurt Reference Acemoglu and Yesilyurt2015) and vesicles (Danker, Vlahovska & Misbah Reference Danker, Vlahovska and Misbah2009; Agarwal & Biros Reference Agarwal and Biros2020).
Zottl & Stark (Reference Zottl and Stark2012) have investigated the influence of a Poiseuille flow on the swinging and tumbling motion of microswimmers in a channel by reducing the problem to a dynamical system for the position and orientation of the swimmer. Using the squirmer model, they found that hydrodynamic interactions between the swimmer and the channel's walls play an important role in stabilising the upstream motion of the swimmer. Notably, they assumed that the swimmer propelled with the velocity ![]() $\boldsymbol {v}=(2B_1/3)\boldsymbol {e}$ of a squirmer in a quiescent flow, where
$\boldsymbol {v}=(2B_1/3)\boldsymbol {e}$ of a squirmer in a quiescent flow, where ![]() $\boldsymbol {e}$ is the swimmer's orientation. The same assumption appears to have been made by Choudhary et al. (Reference Choudhary, Paul, Ruhle and Stark2022) in their analysis of the effects of inertia on the motion of a channel-confined squirmer in a Poiseuille flow. In this study, they showed that inertia and the type of squirmer (neutral pusher/puller) play a critical role in determining the stability of the squirmer's dynamics. The importance of the orientation and motility of swimmers in Poiseuille flows was brought to light by Omori et al. (Reference Omori, Kikuchi, Schmitz, Pavlovic, Chuang and Ishikawa2022) who, through experiments and simulations, investigated the precise mechanism behind the rheotactic behaviour of the shape-changing Chlamydomonas reinhardtii. In their study, the authors assume a time-dependent swimming velocity to account for change in the velocity due to the swimmer's deformation and orientation namely the background flow. To demonstrate the critical role of cell motility on the trajectory and migration of the microorganism, they conduct experiments on motile vs non-motile cells. Their findings revealed that given an initial position off the centreline of the background flow, only motile cells were able to adjust their strokes in order to continuously migrate towards the centreline. The critical role cell motility plays in ciliates’ motion was also investigated by Marumo, Yamagishi & Yajima (Reference Marumo, Yamagishi and Yajima2021) using three-dimensional tracking experiments of free-swimming Tetrahymena. In their study, the authors reported that the non-motile cells, while rotating along their symmetry axis, remain on a straight path from their initial position.
$\boldsymbol {e}$ is the swimmer's orientation. The same assumption appears to have been made by Choudhary et al. (Reference Choudhary, Paul, Ruhle and Stark2022) in their analysis of the effects of inertia on the motion of a channel-confined squirmer in a Poiseuille flow. In this study, they showed that inertia and the type of squirmer (neutral pusher/puller) play a critical role in determining the stability of the squirmer's dynamics. The importance of the orientation and motility of swimmers in Poiseuille flows was brought to light by Omori et al. (Reference Omori, Kikuchi, Schmitz, Pavlovic, Chuang and Ishikawa2022) who, through experiments and simulations, investigated the precise mechanism behind the rheotactic behaviour of the shape-changing Chlamydomonas reinhardtii. In their study, the authors assume a time-dependent swimming velocity to account for change in the velocity due to the swimmer's deformation and orientation namely the background flow. To demonstrate the critical role of cell motility on the trajectory and migration of the microorganism, they conduct experiments on motile vs non-motile cells. Their findings revealed that given an initial position off the centreline of the background flow, only motile cells were able to adjust their strokes in order to continuously migrate towards the centreline. The critical role cell motility plays in ciliates’ motion was also investigated by Marumo, Yamagishi & Yajima (Reference Marumo, Yamagishi and Yajima2021) using three-dimensional tracking experiments of free-swimming Tetrahymena. In their study, the authors reported that the non-motile cells, while rotating along their symmetry axis, remain on a straight path from their initial position.
These studies illustrate the growing interest on the dynamics of swimming microorganisms in Poiseuille flow, focusing on the influence of motility, orientation and shape on the trajectory and motion of the swimmers. However, the assumption of the swimmer propelling at the same velocity it would in a quiescent flow may not hold in a Poiseuille flow, especially since Poiseuille flows introduce hydrodynamic features that significantly affect motions such as vortices (Zottl & Stark Reference Zottl and Stark2012). Moreover, existing studies did not provide information on performance metrics that are critical for the design of artificial microswimmers, such as the work done by swimmers locomoting in Poiseuille flows. These observations reveal that a systematic study of the influence of the Poiseuille flow on the propulsion of biological microorganisms, to derive swimming characteristics and performance metrics akin to those obtained for propulsion in uniform flows (Lighthill Reference Lighthill1952; Blake Reference Blake1971), is lacking.
A Poiseuille flow is obtained by superimposing a uniform flow and a paraboloidal flow, so investigating the influence of paraboloidal flows on the propulsion of microorganisms represents the first key step towards a complete understanding of the influence of Poiseuille flows on microorganisms’ propulsion. Note that, in terms of singularities commonly identified in hydrodynamic studies, a uniform flow past a sphere consists of a Stokeslet and potential dipole at the sphere's centre (Lamb Reference Lamb1945; Happel & Brenner Reference Happel and Brenner1973). On the other hand, for a paraboloidal flow, one needs a Stokeslet, potential dipole, Stokes quadrupole and potential octupole (Chwang & Wu Reference Chwang and Wu1975; Palaniappan & Daripa Reference Palaniappan and Daripa2000). The effects of uniform flows on microorganisms’ propulsion have been disseminated extensively. However, while the influence of paraboloidal flows on spheres (Chwang & Wu Reference Chwang and Wu1975) and droplets (Palaniappan & Daripa Reference Palaniappan and Daripa2000, Reference Palaniappan and Daripa2005) has been studied, to the best of the authors' knowledge its pivotal effects on the performance metrics and swimming characteristics of microorganisms have yet to be explored. The present study addresses this gap in knowledge.
Our paper is organised as follows. We first consider the axisymmetric case in § 2, where the microswimmer is aligned on the centreline of the background flow. After formulating the problem and solving the governing equations, we discuss the various performance metrics including the propulsion speed, power dissipation and swimming efficiency. In § 3 we then analyse the most general case that accounts for the position and orientation of the microswimmer off the centreline of the background flow. Finally, we conclude with few remarks on the implication of our work in § 4.
2. Propulsion along the centreline
We first consider the case of an axisymmetric unbounded paraboloidal flow of strength ![]() $\tilde {U}_p$ whose stream function is given by
$\tilde {U}_p$ whose stream function is given by ![]() $\tilde {\psi }_\infty = \tilde {U}_p r^4\sin ^4\theta /4$ (Jeong Reference Jeong2019) where the
$\tilde {\psi }_\infty = \tilde {U}_p r^4\sin ^4\theta /4$ (Jeong Reference Jeong2019) where the ![]() $(\;\tilde {}\;)$ denotes dimensional variables. The corresponding flow field becomes
$(\;\tilde {}\;)$ denotes dimensional variables. The corresponding flow field becomes
 \begin{equation} \tilde{\boldsymbol{u}}_\infty = \left\langle \frac{1}{r^2\sin\theta}\frac{\partial\tilde{\psi}_\infty}{\partial\theta}, - \frac{1}{r\sin\theta}\frac{\partial\tilde{\psi}_\infty}{\partial r} \right\rangle = \tilde{U}_p\left\langle r^2\sin^2\cos\theta, -r^2\sin^3\theta \right\rangle. \end{equation}
\begin{equation} \tilde{\boldsymbol{u}}_\infty = \left\langle \frac{1}{r^2\sin\theta}\frac{\partial\tilde{\psi}_\infty}{\partial\theta}, - \frac{1}{r\sin\theta}\frac{\partial\tilde{\psi}_\infty}{\partial r} \right\rangle = \tilde{U}_p\left\langle r^2\sin^2\cos\theta, -r^2\sin^3\theta \right\rangle. \end{equation}The microswimmer is modelled as a squirmer with surface velocity (Lighthill Reference Lighthill1952; Blake Reference Blake1971; Pedley Reference Pedley2016)
 \begin{equation} \tilde{\boldsymbol{u}}_{sq} = \sum^\infty_{n=1}A_n P_n(\cos\theta)\boldsymbol{e}_r + \sum^\infty_{n=1}B_nV_n(\cos\theta)\boldsymbol{e}_\theta, \end{equation}
\begin{equation} \tilde{\boldsymbol{u}}_{sq} = \sum^\infty_{n=1}A_n P_n(\cos\theta)\boldsymbol{e}_r + \sum^\infty_{n=1}B_nV_n(\cos\theta)\boldsymbol{e}_\theta, \end{equation}
where ![]() $A_n$ and
$A_n$ and ![]() $B_n$ are the radial and tangential swimming modes, respectively,
$B_n$ are the radial and tangential swimming modes, respectively, ![]() $P_n(\cos \theta )$ are the Legendre polynomials,
$P_n(\cos \theta )$ are the Legendre polynomials, ![]() $V_n(\cos \theta ) = -2/[n(n+1)] P^1_n(\cos \theta )$ and
$V_n(\cos \theta ) = -2/[n(n+1)] P^1_n(\cos \theta )$ and ![]() $P^1_n(\cos \theta )$ are the associated Legendre polynomials. The squirmer translates with velocity
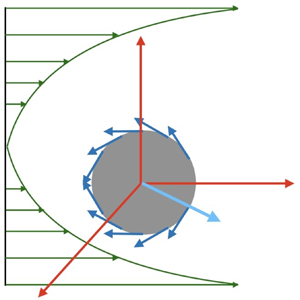
$P^1_n(\cos \theta )$ are the associated Legendre polynomials. The squirmer translates with velocity ![]() $\tilde {U}_s$ and is placed at the centreline of the paraboloidal flow (figure 1). Moreover, we consider the problem in the laboratory frame of reference where the origin of the coordinate system is taken to be at the centre of the squirmer with the parabolic flow evaluated at the origin. In this configuration, the squirmer is translating in a fluid that is quiescent in the far-field (Schonberg & Hinch Reference Schonberg and Hinch1989; Asmolov Reference Asmolov1999; Hood, Lee & Roper Reference Hood, Lee and Roper2015).
$\tilde {U}_s$ and is placed at the centreline of the paraboloidal flow (figure 1). Moreover, we consider the problem in the laboratory frame of reference where the origin of the coordinate system is taken to be at the centre of the squirmer with the parabolic flow evaluated at the origin. In this configuration, the squirmer is translating in a fluid that is quiescent in the far-field (Schonberg & Hinch Reference Schonberg and Hinch1989; Asmolov Reference Asmolov1999; Hood, Lee & Roper Reference Hood, Lee and Roper2015).

Figure 1. A squirmer with surface velocity ![]() $\boldsymbol {u}_{sq}$ propelling with velocity
$\boldsymbol {u}_{sq}$ propelling with velocity ![]() $U_s$ in an unbounded paraboloidal flow with velocity strength
$U_s$ in an unbounded paraboloidal flow with velocity strength ![]() $U_p$. The squirmer is positioned at the centre of the background flow profile, translating along the
$U_p$. The squirmer is positioned at the centre of the background flow profile, translating along the ![]() $\boldsymbol {e}_z$ direction.
$\boldsymbol {e}_z$ direction.
All equations governing the problem are scaled using the squirmer's radius ![]() $a$ for length, the first swimming mode
$a$ for length, the first swimming mode ![]() $B_1$ for velocity, and the ratio
$B_1$ for velocity, and the ratio ![]() $\mu B_1/a$ for pressure (where
$\mu B_1/a$ for pressure (where ![]() $\mu$ is the viscosity of the fluid). Note that in the case of a radial squirmer,
$\mu$ is the viscosity of the fluid). Note that in the case of a radial squirmer, ![]() $A_1$ is used in place of
$A_1$ is used in place of ![]() $B_1$. Given the size of the microswimmer, inertial effects can be omitted and the flow field is governed by the incompressible Stokes equation
$B_1$. Given the size of the microswimmer, inertial effects can be omitted and the flow field is governed by the incompressible Stokes equation
where ![]() $p$ and
$p$ and ![]() $\boldsymbol {u}$ are the pressure and velocity fields of the fluid, respectively. The dimensionless squirmer's surface velocity
$\boldsymbol {u}$ are the pressure and velocity fields of the fluid, respectively. The dimensionless squirmer's surface velocity
 \begin{equation} \boldsymbol{u}_{sq} = \sum^\infty_{n=1}\alpha_n P_n(\cos\theta)\boldsymbol{e}_r + \sum^\infty_{n=1}\beta_nV_n(\cos\theta)\boldsymbol{e}_\theta. \end{equation}
\begin{equation} \boldsymbol{u}_{sq} = \sum^\infty_{n=1}\alpha_n P_n(\cos\theta)\boldsymbol{e}_r + \sum^\infty_{n=1}\beta_nV_n(\cos\theta)\boldsymbol{e}_\theta. \end{equation}
For a radial squirmer (![]() $\beta _n=0$),
$\beta _n=0$), ![]() $\alpha _n=A_n/A_1$ whereas
$\alpha _n=A_n/A_1$ whereas ![]() $\beta _n=B_n/B_1$ for a tangential squirmer (
$\beta _n=B_n/B_1$ for a tangential squirmer (![]() $\alpha _n=0$). Note that the parameters
$\alpha _n=0$). Note that the parameters ![]() $B_1$,
$B_1$, ![]() $B_2$ and
$B_2$ and ![]() $B_3$ are associated with a Stokeslet, a stresslet and a Stokes quadrupole, respectively (Pak & Lauga Reference Pak and Lauga2014). Physically, the
$B_3$ are associated with a Stokeslet, a stresslet and a Stokes quadrupole, respectively (Pak & Lauga Reference Pak and Lauga2014). Physically, the ![]() $B_1$ mode determines the propulsion speed while the
$B_1$ mode determines the propulsion speed while the ![]() $B_2$ mode dominates the far-field flow induced by the swimmer and, typically, captures the swimmer's typologies (neutral, pusher, puller). For this reason, many previous studies have neglected modes beyond
$B_2$ mode dominates the far-field flow induced by the swimmer and, typically, captures the swimmer's typologies (neutral, pusher, puller). For this reason, many previous studies have neglected modes beyond ![]() $n=2$ (Zhu, Lauga & Brandt Reference Zhu, Lauga and Brandt2012; Chisholm et al. Reference Chisholm, Legendre, Lauga and Khair2016; Li, Lauga & Ardekani Reference Li, Lauga and Ardekani2021; Thery, Maab & Lauga Reference Thery, Maab and Lauga2023). The velocity field in the far-field is
$n=2$ (Zhu, Lauga & Brandt Reference Zhu, Lauga and Brandt2012; Chisholm et al. Reference Chisholm, Legendre, Lauga and Khair2016; Li, Lauga & Ardekani Reference Li, Lauga and Ardekani2021; Thery, Maab & Lauga Reference Thery, Maab and Lauga2023). The velocity field in the far-field is
and
on the surface of the squirmer where, after some algebraic manipulations, the dimensionless spatially varying paraboloidal flow can be expressed in the form
with ![]() $U_p = \tilde {U}_p/B_1$ (see Appendix A for details of the derivation). We deduce from (2.7) that the paraboloidal flow will affect the flow field up to order
$U_p = \tilde {U}_p/B_1$ (see Appendix A for details of the derivation). We deduce from (2.7) that the paraboloidal flow will affect the flow field up to order ![]() $n=3$. Thus, while previous studies in uniform flows have justifiably omitted swimming modes
$n=3$. Thus, while previous studies in uniform flows have justifiably omitted swimming modes ![]() $B_{n\geq 3}$, here we consider a three-mode squirmer to fully characterise the effect of paraboloidal flows on swimming.
$B_{n\geq 3}$, here we consider a three-mode squirmer to fully characterise the effect of paraboloidal flows on swimming.
We use Lamb's general solution for the incompressible Stokes equation (Lamb Reference Lamb1945; Happel & Brenner Reference Happel and Brenner1973)
 $$\begin{gather} u_r = \sum^\infty_{n=0}\left(O_n r^{n+1} + Q_n r^{n-1} + \frac{R_n}{r^n} + \frac{S_n}{r^{n+2}}\right) P_n\left(\cos\theta\right), \end{gather}$$
$$\begin{gather} u_r = \sum^\infty_{n=0}\left(O_n r^{n+1} + Q_n r^{n-1} + \frac{R_n}{r^n} + \frac{S_n}{r^{n+2}}\right) P_n\left(\cos\theta\right), \end{gather}$$ $$\begin{gather}u_\theta = \sum^\infty_{n=1}\left(-\frac{n+3}{2}O_n r^{n+1} - \frac{n+1}{2}Q_n r^{n-1} + \frac{n-2}{2}\frac{R_n}{r^n} + \frac{n}{2}\frac{S_n}{r^{n+2}}\right) V_n\left(\cos\theta\right) \end{gather}$$
$$\begin{gather}u_\theta = \sum^\infty_{n=1}\left(-\frac{n+3}{2}O_n r^{n+1} - \frac{n+1}{2}Q_n r^{n-1} + \frac{n-2}{2}\frac{R_n}{r^n} + \frac{n}{2}\frac{S_n}{r^{n+2}}\right) V_n\left(\cos\theta\right) \end{gather}$$
and the boundary conditions to determine the exact flow and pressure fields. The coefficients ![]() $O_n, Q_n, R_n, S_n$ in the general solution are expressed in terms of the propulsion speed
$O_n, Q_n, R_n, S_n$ in the general solution are expressed in terms of the propulsion speed ![]() $U_s$ that, in turn, is obtained by applying the force-free condition on the surface of the squirmer
$U_s$ that, in turn, is obtained by applying the force-free condition on the surface of the squirmer ![]() $S$
$S$ ![]() $(r=1)$
$(r=1)$
where ![]() $\boldsymbol {\sigma }=-p\boldsymbol{\mathsf{I}} + \boldsymbol {\nabla }\boldsymbol {u}+(\boldsymbol {\nabla }\boldsymbol {u})^{\rm T}$,
$\boldsymbol {\sigma }=-p\boldsymbol{\mathsf{I}} + \boldsymbol {\nabla }\boldsymbol {u}+(\boldsymbol {\nabla }\boldsymbol {u})^{\rm T}$, ![]() $\boldsymbol{\mathsf{I}}$ is the identity tensor and
$\boldsymbol{\mathsf{I}}$ is the identity tensor and ![]() $\boldsymbol {n} = \boldsymbol {e}_r$ is the unit outward normal vector. In spherical coordinates the swimming direction
$\boldsymbol {n} = \boldsymbol {e}_r$ is the unit outward normal vector. In spherical coordinates the swimming direction ![]() $\boldsymbol {e}_z=\cos \theta \boldsymbol {e}_r-\sin \theta \boldsymbol {e}_\theta$, and (2.10) reduces to
$\boldsymbol {e}_z=\cos \theta \boldsymbol {e}_r-\sin \theta \boldsymbol {e}_\theta$, and (2.10) reduces to
After lengthy calculations, (2.11) yields the propulsion speed
Equation (2.12) contrasts with the propulsion speed ![]() $\tilde {U}_{uniform}=(2B_1-A_1)/3$ of a spherical squirmer in a uniform flow (Lighthill Reference Lighthill1952; Blake Reference Blake1971). However, the speed remains independent of higher swimming modes
$\tilde {U}_{uniform}=(2B_1-A_1)/3$ of a spherical squirmer in a uniform flow (Lighthill Reference Lighthill1952; Blake Reference Blake1971). However, the speed remains independent of higher swimming modes ![]() $A_{n\geq 2}$ and
$A_{n\geq 2}$ and ![]() $B_{n\geq 2}$. In keeping with previous studies, in the rest of our analysis we only consider the flow field generated by a squirmer with purely tangential surface velocity. The value
$B_{n\geq 2}$. In keeping with previous studies, in the rest of our analysis we only consider the flow field generated by a squirmer with purely tangential surface velocity. The value ![]() $U_p=-1$ corresponds to the propulsion-free case, when the background flow is tuned to negate the first swimming mode
$U_p=-1$ corresponds to the propulsion-free case, when the background flow is tuned to negate the first swimming mode ![]() $B_1$. This configuration is equivalent to the pumping problem (Pak & Lauga Reference Pak and Lauga2014), when the squirmer is held fixed and the flow field is generated solely as a result of interaction between the background flow and the surface velocity.
$B_1$. This configuration is equivalent to the pumping problem (Pak & Lauga Reference Pak and Lauga2014), when the squirmer is held fixed and the flow field is generated solely as a result of interaction between the background flow and the surface velocity.
Substituting ![]() $U_s=2(1+U_p)/3$ and the coefficients
$U_s=2(1+U_p)/3$ and the coefficients ![]() $O_n, Q_n, R_n, S_n$ (
$O_n, Q_n, R_n, S_n$ (![]() $n\leq 3$) into the solutions, the flow field
$n\leq 3$) into the solutions, the flow field ![]() $\boldsymbol {u}=\langle u_r, u_\theta \rangle$ and pressure are obtained as
$\boldsymbol {u}=\langle u_r, u_\theta \rangle$ and pressure are obtained as
 \begin{align} u_r &= \frac{2 \cos\theta }{3 r^3}-\frac{\beta_2 \left(r^2-1\right) (3 \cos2 \theta+1)}{4 r^4}\nonumber\\ &\quad+\beta_3 \left[\frac{\cos \theta (5 \cos2 \theta -1)}{4 r^5}-\frac{\cos \theta (5 \cos2 \theta-1)}{4 r^3}\right] \nonumber\\ &\quad + U_p \frac{\left[3-r^2+3\left(7r^2-5\right)\cos2\theta\right]}{12r^5}\cos\theta, \end{align}
\begin{align} u_r &= \frac{2 \cos\theta }{3 r^3}-\frac{\beta_2 \left(r^2-1\right) (3 \cos2 \theta+1)}{4 r^4}\nonumber\\ &\quad+\beta_3 \left[\frac{\cos \theta (5 \cos2 \theta -1)}{4 r^5}-\frac{\cos \theta (5 \cos2 \theta-1)}{4 r^3}\right] \nonumber\\ &\quad + U_p \frac{\left[3-r^2+3\left(7r^2-5\right)\cos2\theta\right]}{12r^5}\cos\theta, \end{align} \begin{align} u_\theta &= \frac{\sin \theta }{3 r^3} + \frac{\beta_2 \sin \theta \cos\theta }{r^4} -\frac{\beta_3 \left(r^2-3\right) \sin\theta (5 \cos2 \theta +3)}{16 r^5} \nonumber\\ &\quad + U_p \frac{\left[{-}27+19r^2+3\left(7r^2-15\right)\cos2\theta\right]}{48r^5}\sin\theta, \end{align}
\begin{align} u_\theta &= \frac{\sin \theta }{3 r^3} + \frac{\beta_2 \sin \theta \cos\theta }{r^4} -\frac{\beta_3 \left(r^2-3\right) \sin\theta (5 \cos2 \theta +3)}{16 r^5} \nonumber\\ &\quad + U_p \frac{\left[{-}27+19r^2+3\left(7r^2-15\right)\cos2\theta\right]}{48r^5}\sin\theta, \end{align}
Note that in the absence of a background flow (![]() $U_p=0$), the velocity field reduces to that of a squirmer in a quiescent fluid (Lighthill Reference Lighthill1952; Blake Reference Blake1971). The velocity field can also be expressed in the form
$U_p=0$), the velocity field reduces to that of a squirmer in a quiescent fluid (Lighthill Reference Lighthill1952; Blake Reference Blake1971). The velocity field can also be expressed in the form ![]() $\boldsymbol {u}=\langle \partial \psi /\partial \theta /(r^2\sin \theta ),-\partial \psi /\partial r/(r\sin \theta ) \rangle$ where the stream function
$\boldsymbol {u}=\langle \partial \psi /\partial \theta /(r^2\sin \theta ),-\partial \psi /\partial r/(r\sin \theta ) \rangle$ where the stream function
 \begin{align} \psi &= \frac{\sin ^2\theta}{3 r} -\frac{\beta_2 \left(r^2-1\right) \sin ^2\theta \cos \theta}{2 r^2}+\frac{\beta_3 \sin ^2\theta \left[{-}15 \left(r^2-1\right) \cos2 \theta -9 r^2+9\right]}{48 r^3} \nonumber\\ &\quad + U_p \frac{ \sin ^2\theta \left[3 \left(7 r^2-5\right) \cos 2 \theta +19 r^2-9\right]}{48 r^3}. \end{align}
\begin{align} \psi &= \frac{\sin ^2\theta}{3 r} -\frac{\beta_2 \left(r^2-1\right) \sin ^2\theta \cos \theta}{2 r^2}+\frac{\beta_3 \sin ^2\theta \left[{-}15 \left(r^2-1\right) \cos2 \theta -9 r^2+9\right]}{48 r^3} \nonumber\\ &\quad + U_p \frac{ \sin ^2\theta \left[3 \left(7 r^2-5\right) \cos 2 \theta +19 r^2-9\right]}{48 r^3}. \end{align}
To validate our results, we employed physics-informed neural networks (PINNs) to approximate the velocity field for ![]() $U_p=0$, and the propulsion speed
$U_p=0$, and the propulsion speed ![]() $U_s$ for various values of the background flow's maximum velocity (see Appendix B for details). Recall again that paraboloidal flows only affect the first and third terms in Lamb's general solution. Therefore, for
$U_s$ for various values of the background flow's maximum velocity (see Appendix B for details). Recall again that paraboloidal flows only affect the first and third terms in Lamb's general solution. Therefore, for ![]() $n=2$ and
$n=2$ and ![]() $n\geq 4$, the velocity fields generated as a result of squirming in a paraboloidal flow and quiescent fluid are identical.
$n\geq 4$, the velocity fields generated as a result of squirming in a paraboloidal flow and quiescent fluid are identical.
2.1. Flow field
The squirmer propels against the direction of the background flow. Thus, propulsion is along the positive (negative) ![]() $z$ direction when the background flow is directed towards the negative (positive)
$z$ direction when the background flow is directed towards the negative (positive) ![]() $z$ direction (
$z$ direction (![]() $U_p<0$) [(
$U_p<0$) [(![]() $U_p>0$)]. The flow field informs us on the types of hydrodynamic interactions between squirmers and other organisms/particles one can expect. We consider three cases to analyse the flow fields:
$U_p>0$)]. The flow field informs us on the types of hydrodynamic interactions between squirmers and other organisms/particles one can expect. We consider three cases to analyse the flow fields: ![]() $U_p=-2$,
$U_p=-2$, ![]() $U_p=-1$ (no propulsion) and
$U_p=-1$ (no propulsion) and ![]() $U_p=1$. Figure 2 shows the velocity magnitude and streamlines for a neutral squirmer (figure 2a–d) and a pusher with
$U_p=1$. Figure 2 shows the velocity magnitude and streamlines for a neutral squirmer (figure 2a–d) and a pusher with ![]() $\beta _2=-1$ (figure 2e–h). In a quiescent flow (figure 2a), neutral squirmers generate currents that advect particles in front of the swimmer away from the swimmer, whereas particles on the back of the swimmer are pulled towards the swimmer. This dynamics contrasts with that observed in a paraboloidal flow, as illustrated in figures 2(b)–2(d). In these cases, the situation is reversed: particles are drawn towards the swimmer at the front and driven away from its back. This behaviour is consistent across magnitudes of the background flow, including in the absence of propulsion when the flow cancels out the propulsion generated by the squirmer's surface velocity (
$\beta _2=-1$ (figure 2e–h). In a quiescent flow (figure 2a), neutral squirmers generate currents that advect particles in front of the swimmer away from the swimmer, whereas particles on the back of the swimmer are pulled towards the swimmer. This dynamics contrasts with that observed in a paraboloidal flow, as illustrated in figures 2(b)–2(d). In these cases, the situation is reversed: particles are drawn towards the swimmer at the front and driven away from its back. This behaviour is consistent across magnitudes of the background flow, including in the absence of propulsion when the flow cancels out the propulsion generated by the squirmer's surface velocity (![]() $\hat {U}_p=B_1$). For pushers in a quiescent flow (figure 2e), particles are advected away from the swimmer both at the front and back, unless they are at the immediate vicinity of the swimmer's back, in which case the particles are pulled towards the swimmer. This overall dynamic is also observed in paraboloidal flows and across magnitudes of the background flow (figure 2f–h). The flow fields generated by three-mode squirmers show interesting and non-trivial variations that depend on the strength of the third mode
$\hat {U}_p=B_1$). For pushers in a quiescent flow (figure 2e), particles are advected away from the swimmer both at the front and back, unless they are at the immediate vicinity of the swimmer's back, in which case the particles are pulled towards the swimmer. This overall dynamic is also observed in paraboloidal flows and across magnitudes of the background flow (figure 2f–h). The flow fields generated by three-mode squirmers show interesting and non-trivial variations that depend on the strength of the third mode ![]() $\beta _3$. This, in turn, has important implications on the hydrodynamic interactions experienced at the front and back of a three-mode squirmer. Figure 3 shows the velocity magnitude and streamlines for a three-mode squirmer with (figure 3a,b)
$\beta _3$. This, in turn, has important implications on the hydrodynamic interactions experienced at the front and back of a three-mode squirmer. Figure 3 shows the velocity magnitude and streamlines for a three-mode squirmer with (figure 3a,b) ![]() $\beta _3=-1$ and (figure 3c–f)
$\beta _3=-1$ and (figure 3c–f) ![]() $\beta _3=-20$. At
$\beta _3=-20$. At ![]() $\beta _3=-1$ in a uniform flow (figure 3a,c), the interaction dynamics is similar to that of a neutral squirmer: particles are repulsed at the front of the swimmer and attracted at the back. The dynamics is reversed in a paraboloidal flow (figure 3b,d), where this time particles move towards the swimmer's front whereas they are being advected away from its back. The flow field generated by the squirmer becomes nearly identical in uniform flows compared with paraboloidal flows when the magnitude of the swimming mode is increased. Figures 3(e) and 3(f) show the microvortices that are generated during the squirmer's motion. Although their features are similar, the velocity fields of the squirmers differ in their orientation. As a result, while the squirmer repels (draws in) particles at their front (back) in a quiescent fluid, it behaves in the opposite manner in a paraboloidal flow by pulling in (advecting away) particles at its front (back).
$\beta _3=-1$ in a uniform flow (figure 3a,c), the interaction dynamics is similar to that of a neutral squirmer: particles are repulsed at the front of the swimmer and attracted at the back. The dynamics is reversed in a paraboloidal flow (figure 3b,d), where this time particles move towards the swimmer's front whereas they are being advected away from its back. The flow field generated by the squirmer becomes nearly identical in uniform flows compared with paraboloidal flows when the magnitude of the swimming mode is increased. Figures 3(e) and 3(f) show the microvortices that are generated during the squirmer's motion. Although their features are similar, the velocity fields of the squirmers differ in their orientation. As a result, while the squirmer repels (draws in) particles at their front (back) in a quiescent fluid, it behaves in the opposite manner in a paraboloidal flow by pulling in (advecting away) particles at its front (back).

Figure 2. Velocity magnitude and streamlines for (a–d) a neutral squirmer (![]() $\beta _2=0,\beta _3=0$) and (e–h) a pusher (
$\beta _2=0,\beta _3=0$) and (e–h) a pusher (![]() $\beta _2=-1,\beta _3=0$) in a uniform flow (a,e) and in a paraboloidal flow with
$\beta _2=-1,\beta _3=0$) in a uniform flow (a,e) and in a paraboloidal flow with ![]() $U_p=-2$ (b,f),
$U_p=-2$ (b,f), ![]() $U_p=-1$ (c,g) and
$U_p=-1$ (c,g) and ![]() $U_p=1$ (d,h). The streamlines extending through the axis of symmetry
$U_p=1$ (d,h). The streamlines extending through the axis of symmetry ![]() $x=0$ in (e,f,h) denote a separatrix: flow is directed towards the swimmer in the vicinity of the latter, and away from the swimmer in the far field. This is represented by the arrows. The colour bar represents the magnitude of the velocity field.
$x=0$ in (e,f,h) denote a separatrix: flow is directed towards the swimmer in the vicinity of the latter, and away from the swimmer in the far field. This is represented by the arrows. The colour bar represents the magnitude of the velocity field.

Figure 3. Velocity magnitude and streamlines for a three-mode squirmer with (a–d) ![]() $\beta _2=0,\beta _3=-1$ and (e,f)
$\beta _2=0,\beta _3=-1$ and (e,f) ![]() $\beta _2=0,\beta _3=-20$ in a uniform flow (a,c,e) and in a paraboloidal flow with
$\beta _2=0,\beta _3=-20$ in a uniform flow (a,c,e) and in a paraboloidal flow with ![]() $U_p=-2$ (b) and
$U_p=-2$ (b) and ![]() $U_p=1$ (d,f). The colour bar represents the magnitude of the velocity field. The (
$U_p=1$ (d,f). The colour bar represents the magnitude of the velocity field. The (![]() $\star$) symbols on either side of the squirmer in (b,f) denote the location of stagnation points, given by (2.17).
$\star$) symbols on either side of the squirmer in (b,f) denote the location of stagnation points, given by (2.17).
An interesting feature that also influences hydrodynamic interactions are vortices (or eddies). They have been reported for pushers and pullers with rotational velocities near a wall or flat plate (Drescher et al. Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009; Poddar, Bandopadhyay & Chakraborty Reference Poddar, Bandopadhyay and Chakraborty2020) and in the feeding patterns of starfish (Gilpin, Prakash & Prakash Reference Gilpin, Prakash and Prakash2017). In unbounded domains, these microvortices appear to be a signature of three-mode squirmers with large ![]() $\beta _3$ in both uniform flows (see Gilpin et al. (Reference Gilpin, Prakash and Prakash2017) and figure 3e) and paraboloidal flows (figure 3f).
$\beta _3$ in both uniform flows (see Gilpin et al. (Reference Gilpin, Prakash and Prakash2017) and figure 3e) and paraboloidal flows (figure 3f).
Moreover, while microvortices are not present for three-mode squirmers in quiescent fluids with relatively small ![]() $\beta _3$, their presence in paraboloidal flows shows a dependence on the strength of the background flow. Specifically, microvortices are only observed for three-mode squirmers with small
$\beta _3$, their presence in paraboloidal flows shows a dependence on the strength of the background flow. Specifically, microvortices are only observed for three-mode squirmers with small ![]() $\beta _3$ and
$\beta _3$ and ![]() $U_p<0$, as illustrated in figure 3(b). The existence of vortical regions in the flow field of neutral squirmers and pushers present yet another significant difference between propulsion in uniform flows vs paraboloidal flows. Indeed, the microvortices in figure 2(b,c) for neutral squirmers and figure 2(f) for pushers are a direct consequence of the paraboloidal flows. These flows introduce a Stokes quadrupole in the near-field, resulting in flow patterns similar to those generated by three-mode squirmers with small
$U_p<0$, as illustrated in figure 3(b). The existence of vortical regions in the flow field of neutral squirmers and pushers present yet another significant difference between propulsion in uniform flows vs paraboloidal flows. Indeed, the microvortices in figure 2(b,c) for neutral squirmers and figure 2(f) for pushers are a direct consequence of the paraboloidal flows. These flows introduce a Stokes quadrupole in the near-field, resulting in flow patterns similar to those generated by three-mode squirmers with small ![]() $\beta _3$ and
$\beta _3$ and ![]() $U_p<0$ (figure 3b) or more generally with large
$U_p<0$ (figure 3b) or more generally with large ![]() $\beta _3$ (figure 3f). Here we note that the flow field in a uniform flow has zero vorticity, whereas in a paraboloidal flow the vorticity
$\beta _3$ (figure 3f). Here we note that the flow field in a uniform flow has zero vorticity, whereas in a paraboloidal flow the vorticity ![]() $\boldsymbol {\nabla }\times \boldsymbol {u}\neq \boldsymbol {0}$. We further remark that vortices, like flow reversals, often point to stagnation points
$\boldsymbol {\nabla }\times \boldsymbol {u}\neq \boldsymbol {0}$. We further remark that vortices, like flow reversals, often point to stagnation points ![]() $(x^*, z^*) = (r_s\sin \theta,r_s\cos \theta )$ in the flow. For three-mode squirmers with
$(x^*, z^*) = (r_s\sin \theta,r_s\cos \theta )$ in the flow. For three-mode squirmers with ![]() $\beta _2=0$, figure 3(b,e,f) indicates that stagnation points exist along the
$\beta _2=0$, figure 3(b,e,f) indicates that stagnation points exist along the ![]() $x$-axis (
$x$-axis (![]() $\theta ={\rm \pi} /2$), where
$\theta ={\rm \pi} /2$), where ![]() $u_r=0$. After setting
$u_r=0$. After setting ![]() $u_\theta =0$, the stagnation points are found to depend on the magnitude of the
$u_\theta =0$, the stagnation points are found to depend on the magnitude of the ![]() $\beta _3$ mode and on the strength of the background flow. The radius
$\beta _3$ mode and on the strength of the background flow. The radius ![]() $r_s$ is given by
$r_s$ is given by
 \begin{equation} r_s ={\pm} 3\sqrt{\frac{\beta_3-U_p}{8+3\beta_3-U_p}}, \end{equation}
\begin{equation} r_s ={\pm} 3\sqrt{\frac{\beta_3-U_p}{8+3\beta_3-U_p}}, \end{equation}
and the stagnation points are represented by the ![]() $\star$ symbols in figures 3(b) and 3(f).
$\star$ symbols in figures 3(b) and 3(f).
2.2. Power dissipation and swimming efficiency
In this section, we discuss the work done by the squirmer and its efficiency. The power dissipation is given by ![]() $\mathcal {P}=-\int _S\boldsymbol {\sigma }\boldsymbol {\cdot }\boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {n}\,{\rm d}S$. In spherical coordinates,
$\mathcal {P}=-\int _S\boldsymbol {\sigma }\boldsymbol {\cdot }\boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {n}\,{\rm d}S$. In spherical coordinates, ![]() $\mathcal {P}$ is expressed as
$\mathcal {P}$ is expressed as
Note that for the axisymmetric motion considered here, ![]() $\sigma _{r\phi }=0$,
$\sigma _{r\phi }=0$, ![]() $u_\phi =0$. After some calculations, we obtain
$u_\phi =0$. After some calculations, we obtain
Equation (2.19) contrasts with the power dissipation ![]() $\mathcal {P}_{uniform} = 8{\rm \pi} (2+\beta _2^2+\beta _3^2/2)/3$ of a squirmer in a uniform flow (Lighthill Reference Lighthill1952; Blake Reference Blake1971). Moreover, we observe that the power dissipation varies not only as a function of the swimming modes, but also as a function of the background flow's strength. For a neutral squirmer (
$\mathcal {P}_{uniform} = 8{\rm \pi} (2+\beta _2^2+\beta _3^2/2)/3$ of a squirmer in a uniform flow (Lighthill Reference Lighthill1952; Blake Reference Blake1971). Moreover, we observe that the power dissipation varies not only as a function of the swimming modes, but also as a function of the background flow's strength. For a neutral squirmer (![]() $\beta _2=\beta _3=0$) with
$\beta _2=\beta _3=0$) with ![]() $U_p=0$, we recover
$U_p=0$, we recover ![]() $\mathcal {P}_{uniform}=16{\rm \pi} /3$. When
$\mathcal {P}_{uniform}=16{\rm \pi} /3$. When ![]() $U_p<-16/7$ or
$U_p<-16/7$ or ![]() $U_p>0$, a neutral squirmer in a paraboloidal flow expends more energy compared with its counterpart in a uniform flow. However, swimming in a paraboloidal flow becomes more beneficial for the squirmer provided
$U_p>0$, a neutral squirmer in a paraboloidal flow expends more energy compared with its counterpart in a uniform flow. However, swimming in a paraboloidal flow becomes more beneficial for the squirmer provided ![]() $U_p\in (-16/7,0)$. We can similarly compare the power dissipation for pushers/pullers (
$U_p\in (-16/7,0)$. We can similarly compare the power dissipation for pushers/pullers (![]() $\beta _3=0$) in paraboloidal flows relative to their work in uniform flows. Figure 4(a) shows the paraboloidal-to-uniform ratio
$\beta _3=0$) in paraboloidal flows relative to their work in uniform flows. Figure 4(a) shows the paraboloidal-to-uniform ratio ![]() $\varepsilon =\mathcal {P}/\mathcal {P}_{uniform}$ for a range of
$\varepsilon =\mathcal {P}/\mathcal {P}_{uniform}$ for a range of ![]() $\beta _2$ values with flow strength
$\beta _2$ values with flow strength ![]() $U_p=-3$ (solid),
$U_p=-3$ (solid), ![]() $U_p=-2$ (dashed) and
$U_p=-2$ (dashed) and ![]() $U_p=1$ (dash-dotted). As expected from the analysis of the neutral squirmer, pushers/pullers always expend less energy compared with their counterparts in uniform flows for
$U_p=1$ (dash-dotted). As expected from the analysis of the neutral squirmer, pushers/pullers always expend less energy compared with their counterparts in uniform flows for ![]() $U_p=-2$.
$U_p=-2$.

Figure 4. Paraboloidal-to-uniform ratios of (a) power dissipation and (b) swimming efficiency as a function of the ![]() $\beta _2$ swimming mode for various strengths of the paraboloidal background flow
$\beta _2$ swimming mode for various strengths of the paraboloidal background flow ![]() $U_p$.
$U_p$.
Before discussing three-mode squirmers, we analyse the efficiency for two-mode squirmers. The swimming efficiency ![]() $\eta = F_DU_s/\mathcal {P}$ (Lighthill Reference Lighthill1952), where
$\eta = F_DU_s/\mathcal {P}$ (Lighthill Reference Lighthill1952), where ![]() $F_D=F_D^p+F_D^s = 4{\rm \pi} U_p+6{\rm \pi} U_s$ is the force required to drag a rigid sphere at the swimming speed in the same fluid medium. Here,
$F_D=F_D^p+F_D^s = 4{\rm \pi} U_p+6{\rm \pi} U_s$ is the force required to drag a rigid sphere at the swimming speed in the same fluid medium. Here, ![]() $F_D^p$ alone is the drag force experienced by a rigid sphere in a paraboloidal flow (Chwang & Wu Reference Chwang and Wu1975) while
$F_D^p$ alone is the drag force experienced by a rigid sphere in a paraboloidal flow (Chwang & Wu Reference Chwang and Wu1975) while ![]() $F_D^s$ is the Stokes drag in the absence of a paraboloidal background flow. After some simplification, the efficiency is given by
$F_D^s$ is the Stokes drag in the absence of a paraboloidal background flow. After some simplification, the efficiency is given by
Figure 4(b) shows the ratio ![]() $\nu =\eta /\eta _{uniform}$ for the flow strengths in figure 4(a). In this case, the efficiency of a swimmer in a uniform flow is given by
$\nu =\eta /\eta _{uniform}$ for the flow strengths in figure 4(a). In this case, the efficiency of a swimmer in a uniform flow is given by ![]() $\eta _{uniform} = 1/(2+\beta _2^2+\beta _3^2/2)$ (Lighthill Reference Lighthill1952; Blake Reference Blake1971). We conclude from the results that all two-mode squirmers in paraboloidal flows experience a gain in swimming efficiency (
$\eta _{uniform} = 1/(2+\beta _2^2+\beta _3^2/2)$ (Lighthill Reference Lighthill1952; Blake Reference Blake1971). We conclude from the results that all two-mode squirmers in paraboloidal flows experience a gain in swimming efficiency (![]() $\nu >1$), except for
$\nu >1$), except for ![]() $U_p=-1/2,-1$. For
$U_p=-1/2,-1$. For ![]() $U_p=-1$ the efficiency is zero since the squirmer does not propel (
$U_p=-1$ the efficiency is zero since the squirmer does not propel (![]() $U_s=0$). On the other hand, efficiency is also zero when
$U_s=0$). On the other hand, efficiency is also zero when ![]() $U_p=-1/2$ (the drag forces
$U_p=-1/2$ (the drag forces ![]() $F_D^p$ and
$F_D^p$ and ![]() $F_D^s$ cancel each other out).
$F_D^s$ cancel each other out).
In the case of a three-mode squirmer, we produce the ![]() $\beta _2-\beta _3$ parameter space (figure 5) to determine the conditions under which the addition of the third swimming mode may yield behaviour distinct from that of a two-mode squirmer. In this analysis, we consider
$\beta _2-\beta _3$ parameter space (figure 5) to determine the conditions under which the addition of the third swimming mode may yield behaviour distinct from that of a two-mode squirmer. In this analysis, we consider ![]() $U_p=-2$. On one hand, figure 5(a) shows that squirmers in a paraboloidal flow expend more energy when
$U_p=-2$. On one hand, figure 5(a) shows that squirmers in a paraboloidal flow expend more energy when ![]() $\beta _3\gtrapprox 0.5$. On the other hand, while the ratio
$\beta _3\gtrapprox 0.5$. On the other hand, while the ratio ![]() $\varepsilon$ may vary depending on
$\varepsilon$ may vary depending on ![]() $\beta _3$, figure 5(b) shows that
$\beta _3$, figure 5(b) shows that ![]() $\nu >1$ for a three-mode squirmer. Thus, despite
$\nu >1$ for a three-mode squirmer. Thus, despite ![]() $\varepsilon$ being greater than unity, the three-mode squirmer is always a more efficient swimmer in paraboloidal flows compared with uniform flows.
$\varepsilon$ being greater than unity, the three-mode squirmer is always a more efficient swimmer in paraboloidal flows compared with uniform flows.

Figure 5. Parameter space of ![]() $(\beta _2,\beta _3)$ for the paraboloidal-to-uniform ratios of power dissipation (a) and efficiency (b) for a three-mode squirmer with
$(\beta _2,\beta _3)$ for the paraboloidal-to-uniform ratios of power dissipation (a) and efficiency (b) for a three-mode squirmer with ![]() $U_p=-2$. The intersection of the vertical lines correspond to the combination
$U_p=-2$. The intersection of the vertical lines correspond to the combination ![]() $(\beta _2,\beta _3)$ at which a two-mode squirmer in a paraboloidal is a more ideal swimmer than a three-mode squirmer in a uniform flow.
$(\beta _2,\beta _3)$ at which a two-mode squirmer in a paraboloidal is a more ideal swimmer than a three-mode squirmer in a uniform flow.
The parameter spaces in figure 5 are subdivided into distinct spheroidal-shaped ‘holes’ or ‘sinks’, especially in the regions ![]() $\beta _3<0.5$ for the swimming efficiency (figure 5b). The smallest of these sinks
$\beta _3<0.5$ for the swimming efficiency (figure 5b). The smallest of these sinks ![]() $\mathcal {S}$ contains the combinations
$\mathcal {S}$ contains the combinations ![]() $(\beta _2,\beta _3)$ that minimise power dissipation and maximise swimming efficiency. The location of the epicentre of
$(\beta _2,\beta _3)$ that minimise power dissipation and maximise swimming efficiency. The location of the epicentre of ![]() $\mathcal {S}$ is
$\mathcal {S}$ is ![]() $(0,38U_p/35)$, as illustrated by the intersection of the dashed lines in figure 5. The case
$(0,38U_p/35)$, as illustrated by the intersection of the dashed lines in figure 5. The case ![]() $\beta _3=38U_p/35$ corresponds to the non-zero value that eliminates the expression
$\beta _3=38U_p/35$ corresponds to the non-zero value that eliminates the expression ![]() $35\beta _3^2-38U_p\beta _3$ in (2.19) and (2.20). In other words, at this value a three-mode squirmer in a paraboloidal flow expends the same energy and swims as efficiently as a two-mode squirmer subject to the same background flow. This suggests that squirmers in paraboloidal flows may be able to take advantage of the background flow to lower their rate of work and become more efficient swimmers. In terms of artificial microswimmers, our findings raise the possibility of novel design principles for microrobots that take advantage of specific properties of the background flow to reduce their work.
$35\beta _3^2-38U_p\beta _3$ in (2.19) and (2.20). In other words, at this value a three-mode squirmer in a paraboloidal flow expends the same energy and swims as efficiently as a two-mode squirmer subject to the same background flow. This suggests that squirmers in paraboloidal flows may be able to take advantage of the background flow to lower their rate of work and become more efficient swimmers. In terms of artificial microswimmers, our findings raise the possibility of novel design principles for microrobots that take advantage of specific properties of the background flow to reduce their work.
To conclude this section, we discuss the potential biological relevance of these results. The first swimming mode ![]() $B_1$ can be approximated using
$B_1$ can be approximated using ![]() $B_1=3\tilde {U}_s/2$ where
$B_1=3\tilde {U}_s/2$ where ![]() $\tilde {U}_s$ is obtained from experimental measurements of the velocity of various microorganisms including ciliates (Rodrigues, Lisicki & Lauga Reference Rodrigues, Lisicki and Lauga2021). Values of the
$\tilde {U}_s$ is obtained from experimental measurements of the velocity of various microorganisms including ciliates (Rodrigues, Lisicki & Lauga Reference Rodrigues, Lisicki and Lauga2021). Values of the ![]() $\beta _2=B_2/B_1$ swimming modes have been estimated previously for artificial and biological swimmers (Evans et al. Reference Evans, Ishikawa, Yamaguchi and Lauga2011). In general, they range from
$\beta _2=B_2/B_1$ swimming modes have been estimated previously for artificial and biological swimmers (Evans et al. Reference Evans, Ishikawa, Yamaguchi and Lauga2011). In general, they range from ![]() $-1$ ( Escherichia coli Drescher et al. Reference Drescher, Dunkel, Cisneros, Ganguly and Goldstein2011), to
$-1$ ( Escherichia coli Drescher et al. Reference Drescher, Dunkel, Cisneros, Ganguly and Goldstein2011), to ![]() $\approx$0 (Volvox Short et al. (Reference Short, Solari, Ganguly, Powers, Kessler and Goldstein2006) and artificially created squirmers such as autonomous vesicles Miura et al. (Reference Miura, Oosawa, Sakai, Syundou, Ban and Shioi2010) or squirming droplets Thutupalli, Seemann & Herminghaus Reference Thutupalli, Seemann and Herminghaus2011), to 1 (Chlamydomonas Pedley & Kessler Reference Pedley and Kessler1990). This range of
$\approx$0 (Volvox Short et al. (Reference Short, Solari, Ganguly, Powers, Kessler and Goldstein2006) and artificially created squirmers such as autonomous vesicles Miura et al. (Reference Miura, Oosawa, Sakai, Syundou, Ban and Shioi2010) or squirming droplets Thutupalli, Seemann & Herminghaus Reference Thutupalli, Seemann and Herminghaus2011), to 1 (Chlamydomonas Pedley & Kessler Reference Pedley and Kessler1990). This range of ![]() $\beta _2$ values lies squarely in the region of least power expenditure and greatest efficiency found in figure 5. Biological microorganisms naturally strive to optimise their motion, and our results capture this behaviour. To the best of the authors’ knowledge, measurements of higher swimming modes have not been performed on biological microorganisms. Moreover, higher modes lead to greater energy expenditure and less efficient swimming. Our results, however, raise the possibility of designing still-efficient artificial microswimmers. Specifically, the later can be built by accounting for the properties of the background flow such that adding a third swimming mode with
$\beta _2$ values lies squarely in the region of least power expenditure and greatest efficiency found in figure 5. Biological microorganisms naturally strive to optimise their motion, and our results capture this behaviour. To the best of the authors’ knowledge, measurements of higher swimming modes have not been performed on biological microorganisms. Moreover, higher modes lead to greater energy expenditure and less efficient swimming. Our results, however, raise the possibility of designing still-efficient artificial microswimmers. Specifically, the later can be built by accounting for the properties of the background flow such that adding a third swimming mode with ![]() $B_3\approx \tilde {U}_p$ does not increase (decrease) the power dissipation (swimming efficiency) of the microswimmer compared with a swimmer with only the first two modes. In addition to minimising work, the carefully added swimming gait could serve other purposes such as aiding in the transport of cargo (Ouyang et al. Reference Ouyang, Lin, Lin, Yu and Phan-Thien2023).
$B_3\approx \tilde {U}_p$ does not increase (decrease) the power dissipation (swimming efficiency) of the microswimmer compared with a swimmer with only the first two modes. In addition to minimising work, the carefully added swimming gait could serve other purposes such as aiding in the transport of cargo (Ouyang et al. Reference Ouyang, Lin, Lin, Yu and Phan-Thien2023).
3. A note on the propulsion of an off-centred squirmer
Results presented in § 2 apply to the propulsion of a squirmer located on the centreline of the paraboloidal flow, in which case the swimmer can only propel along the background flow direction ![]() $\boldsymbol {e}_z$. For completeness, we now consider the case of a squirmer that is positioned off the centreline of the background flow. The latter is located at a distance
$\boldsymbol {e}_z$. For completeness, we now consider the case of a squirmer that is positioned off the centreline of the background flow. The latter is located at a distance ![]() $(x_0,y_0)$ from the origin (figure 6). We specifically focus on determining the translational and rotational velocities of the squirmer in this general case.
$(x_0,y_0)$ from the origin (figure 6). We specifically focus on determining the translational and rotational velocities of the squirmer in this general case.

Figure 6. A squirmer with radius ![]() $a$ and surface velocity
$a$ and surface velocity ![]() $\boldsymbol {u}_{sq}$ off the centreline of a paraboloidal flow located a distance
$\boldsymbol {u}_{sq}$ off the centreline of a paraboloidal flow located a distance ![]() $(x_0,y_0)$ from the origin.
$(x_0,y_0)$ from the origin.
The paraboloidal flow in Cartesian coordinates is given by (Chwang & Wu Reference Chwang and Wu1975)
Expanding the quadrating terms and simplifying yields the paraboloidal flow in spherical coordinates
where ![]() $\dot {\gamma }_1=2x_0$ and
$\dot {\gamma }_1=2x_0$ and ![]() $\dot {\gamma }_2=2y_0$ are local shear rates and
$\dot {\gamma }_2=2y_0$ are local shear rates and ![]() $\varGamma =x_0^2+y_0^2$. Equation (3.2) reveals that in addition to the paraboloidal flow
$\varGamma =x_0^2+y_0^2$. Equation (3.2) reveals that in addition to the paraboloidal flow ![]() $\bar {U}_{p}r^2\sin ^2\theta \boldsymbol {e}_z$, the off-centred squirmer experiences a linear shear flow
$\bar {U}_{p}r^2\sin ^2\theta \boldsymbol {e}_z$, the off-centred squirmer experiences a linear shear flow ![]() $-\bar {U}_{p}r\sin \theta (\dot {\gamma }_1\cos \phi + \dot {\gamma }_1\sin \phi ) \boldsymbol {e}_z$ and a uniform flow
$-\bar {U}_{p}r\sin \theta (\dot {\gamma }_1\cos \phi + \dot {\gamma }_1\sin \phi ) \boldsymbol {e}_z$ and a uniform flow ![]() $\bar {U}_{p}\varGamma \boldsymbol {e}_z$ (Chwang & Wu Reference Chwang and Wu1975; Hanna & Vlahovska Reference Hanna and Vlahovska2010). We observe immediately that positioning the squirmer off the centreline of the background flow introduces a rotational motion in the azimuthal direction
$\bar {U}_{p}\varGamma \boldsymbol {e}_z$ (Chwang & Wu Reference Chwang and Wu1975; Hanna & Vlahovska Reference Hanna and Vlahovska2010). We observe immediately that positioning the squirmer off the centreline of the background flow introduces a rotational motion in the azimuthal direction ![]() $\boldsymbol {e}_\phi$ that results from the linear shear flow. The boundary conditions in the laboratory frame become
$\boldsymbol {e}_\phi$ that results from the linear shear flow. The boundary conditions in the laboratory frame become
where ![]() $\boldsymbol {x}_s = a\boldsymbol {e}_r$ and
$\boldsymbol {x}_s = a\boldsymbol {e}_r$ and ![]() $\hat {\boldsymbol {\varOmega }}_s = \hat {\varOmega }_s\boldsymbol {e}_k$ is the rotational velocity of the squirmer obtained by imposing the torque-free condition
$\hat {\boldsymbol {\varOmega }}_s = \hat {\varOmega }_s\boldsymbol {e}_k$ is the rotational velocity of the squirmer obtained by imposing the torque-free condition
As in § 2, the translational velocity ![]() $\hat {\boldsymbol {U}}_s = \hat {U}_s\boldsymbol {e}_k$ is obtained using the force-free condition (2.10). The index
$\hat {\boldsymbol {U}}_s = \hat {U}_s\boldsymbol {e}_k$ is obtained using the force-free condition (2.10). The index ![]() $k$ denotes the coordinates
$k$ denotes the coordinates ![]() $x,y,z$, so the translational and rotational velocities can occur in any direction. The generalised surface velocity
$x,y,z$, so the translational and rotational velocities can occur in any direction. The generalised surface velocity ![]() $\hat {\boldsymbol {u}}_{sq}$ for the purely tangential squirming motion is given by (Pak & Lauga Reference Pak and Lauga2014)
$\hat {\boldsymbol {u}}_{sq}$ for the purely tangential squirming motion is given by (Pak & Lauga Reference Pak and Lauga2014)
 \begin{align} u_{sq,\theta} &= \sum^\infty_{n=1} \sum^n_{m=0} \left[ -\frac{2\sin\theta P^{m'}_n}{na^{n+2}}\left( B_{mn}\cos m\phi + \hat{B}_{mn} \sin m\phi \right) \right. \nonumber\\ &\quad +\left. \frac{m P^m_n}{a^{n+1}\sin\theta} \left( \hat{C}_{mn}\cos m\phi - C_{mn} \sin m\phi \right) \right] \end{align}
\begin{align} u_{sq,\theta} &= \sum^\infty_{n=1} \sum^n_{m=0} \left[ -\frac{2\sin\theta P^{m'}_n}{na^{n+2}}\left( B_{mn}\cos m\phi + \hat{B}_{mn} \sin m\phi \right) \right. \nonumber\\ &\quad +\left. \frac{m P^m_n}{a^{n+1}\sin\theta} \left( \hat{C}_{mn}\cos m\phi - C_{mn} \sin m\phi \right) \right] \end{align} \begin{align} u_{sq,\phi} &= \sum^\infty_{n=1} \sum^n_{m=0} \left[ \frac{2m P^{m}_n}{na^{n+2}\sin\theta}\left( \hat{B}_{mn}\cos m\phi - B_{mn} \sin m\phi \right) \right. \nonumber\\ &\quad +\left. \frac{\sin\theta P^{m'}_n}{a^{n+1}} \left( C_{mn}\cos m\phi + \hat{C}_{mn} \sin m\phi \right) \right], \end{align}
\begin{align} u_{sq,\phi} &= \sum^\infty_{n=1} \sum^n_{m=0} \left[ \frac{2m P^{m}_n}{na^{n+2}\sin\theta}\left( \hat{B}_{mn}\cos m\phi - B_{mn} \sin m\phi \right) \right. \nonumber\\ &\quad +\left. \frac{\sin\theta P^{m'}_n}{a^{n+1}} \left( C_{mn}\cos m\phi + \hat{C}_{mn} \sin m\phi \right) \right], \end{align}
where ![]() $P^m_n = P^m_n(\cos \theta )$ are the associated Legendre polynomials and
$P^m_n = P^m_n(\cos \theta )$ are the associated Legendre polynomials and ![]() $B_{mn}$,
$B_{mn}$, ![]() $\hat {B}_{mn}$,
$\hat {B}_{mn}$, ![]() $C_{mn}$ and
$C_{mn}$ and ![]() $\hat {C}_{mn}$ are the squirming modes.
$\hat {C}_{mn}$ are the squirming modes.
We use Lamb's general solution for exterior problems (Pak & Lauga Reference Pak and Lauga2014) and apply the boundary conditions to obtain the velocity field ![]() $\boldsymbol {u}=\langle u_r,u_\theta,u_\phi \rangle$ for the general squirming motion of a three-mode squirmer (up to squirming modes
$\boldsymbol {u}=\langle u_r,u_\theta,u_\phi \rangle$ for the general squirming motion of a three-mode squirmer (up to squirming modes ![]() $B_{03}$ and
$B_{03}$ and ![]() $C_{03}$) in paraboloidal flows. The components of the velocity field are given by (C5)–(C7) in Appendix C. After applying the force- and torque-free conditions ((2.10) and (3.5)), lengthy calculations yield the translational and rotational velocities
$C_{03}$) in paraboloidal flows. The components of the velocity field are given by (C5)–(C7) in Appendix C. After applying the force- and torque-free conditions ((2.10) and (3.5)), lengthy calculations yield the translational and rotational velocities
The translational velocity due to purely tangential surface velocity in (2.12) is recovered by using a simple rescaling ![]() $B_{01}=-a^3B_1/2$,
$B_{01}=-a^3B_1/2$, ![]() $\bar {U}_p = U_p/a^2$ and setting
$\bar {U}_p = U_p/a^2$ and setting ![]() $\varGamma =0$,
$\varGamma =0$, ![]() $B_{11}=\hat {B}_{11}=0$. Moreover, in the absence of a paraboloidal flow (
$B_{11}=\hat {B}_{11}=0$. Moreover, in the absence of a paraboloidal flow (![]() $\bar {U}_p=0$) the translational and rotational velocities agree with the results obtained using the reciprocal theorem (Pak & Lauga Reference Pak and Lauga2014). Note that the propulsion of the off-centred squirmer becomes restricted to the
$\bar {U}_p=0$) the translational and rotational velocities agree with the results obtained using the reciprocal theorem (Pak & Lauga Reference Pak and Lauga2014). Note that the propulsion of the off-centred squirmer becomes restricted to the ![]() $x-y$ plane when the strength of the paraboloidal flow
$x-y$ plane when the strength of the paraboloidal flow ![]() $\bar {U}_p = 4 B_{01}/a^3(2a^2+3\varGamma )$.
$\bar {U}_p = 4 B_{01}/a^3(2a^2+3\varGamma )$.
The power dissipation is calculated using (2.18), and can be expressed in terms of contributions from the quiescent and background flows: ![]() $\mathcal {P} = \mathcal {P}_{uniform} + \mathcal {P}_{\bar {U}_p}$. In this case,
$\mathcal {P} = \mathcal {P}_{uniform} + \mathcal {P}_{\bar {U}_p}$. In this case, ![]() $\mathcal {P}_{uniform}$ is the expression obtained by Pak & Lauga (Reference Pak and Lauga2014) for a non-axisymmetric squirmer (equation (77) in their paper) whereas
$\mathcal {P}_{uniform}$ is the expression obtained by Pak & Lauga (Reference Pak and Lauga2014) for a non-axisymmetric squirmer (equation (77) in their paper) whereas ![]() $\mathcal {P}_{\bar {U}_p}$ is given by
$\mathcal {P}_{\bar {U}_p}$ is given by
 \begin{align} \mathcal{P}_{\bar{U}_p} &= {\rm \pi}\mu \left\{ -\frac{4}{105} \left[ 224B_{01} + \frac{72}{a^2}B_{03} - \frac{252}{a^2}\left( \dot{\gamma}_1 B_{12}+\dot{\gamma}_2\hat{B}_{12} \right) \right] \bar{U}_p\right. \nonumber\\ &\quad +\left. \frac{4 a^3}{105}\left[41a^2 + 42\left(\dot{\gamma}_1^2+\dot{\gamma}_2^2\right) \right] \bar{U}_p^2 \right\}. \end{align}
\begin{align} \mathcal{P}_{\bar{U}_p} &= {\rm \pi}\mu \left\{ -\frac{4}{105} \left[ 224B_{01} + \frac{72}{a^2}B_{03} - \frac{252}{a^2}\left( \dot{\gamma}_1 B_{12}+\dot{\gamma}_2\hat{B}_{12} \right) \right] \bar{U}_p\right. \nonumber\\ &\quad +\left. \frac{4 a^3}{105}\left[41a^2 + 42\left(\dot{\gamma}_1^2+\dot{\gamma}_2^2\right) \right] \bar{U}_p^2 \right\}. \end{align}
Equation (3.11) shows that the power dissipation depends explicitly on the linear shear flow, generated as a result of the position of the squirmer relative to the paraboloidal flow's centreline. This result contrasts with (3.9) and (3.10) that do not depend on the local shear rates ![]() $\dot {\gamma }_1$ or
$\dot {\gamma }_1$ or ![]() $\dot {\gamma }_2$, and suggest that the linear shear flow does not influence the translational and rotational velocities of the squirmer. In terms of the dependence on shear flow, our conclusion about the translational velocity is akin to the result obtained by Pak, Feng & Stone (Reference Pak, Feng and Stone2014) in the case of a surfactant-covered drop in a Poiseuille flow.
$\dot {\gamma }_2$, and suggest that the linear shear flow does not influence the translational and rotational velocities of the squirmer. In terms of the dependence on shear flow, our conclusion about the translational velocity is akin to the result obtained by Pak, Feng & Stone (Reference Pak, Feng and Stone2014) in the case of a surfactant-covered drop in a Poiseuille flow.
4. Concluding remarks
In this paper, we have investigated the propulsion of a spherical ciliated microorganism, represented by a squirmer, in a paraboloidal flow. First, we considered the axisymmetric problem. We have obtained exact analytical solutions of the propulsion speed, power dissipation, swimming efficiency, flow and pressure fields, and contrasted our results with those of Lighthill, the long-standing benchmark for microswimming studies in uniform flows. We have found that while the propulsion speed ![]() $U_s=2(1+U_p)/3$ only depends on the first swimming mode (as it does for propulsion in uniform flows first reported by Lighthill Reference Lighthill1952; Blake Reference Blake1971), it is now influenced by the strength of the background flow. The dependence on the maximum velocity of the paraboloidal flow played a significant role in the amount of work being experienced by the squirmer. However, although we have determined the range of flow strength that minimises work, we have shown that squirmers in paraboloidal flows are always more efficient compared with squirmers in uniform flows. We then considered the more general, non-axisymmetric problem of a squirmer off the centreline of the background flow. In this framework, the shear-induced orientation and rotation of the squirmer now enter the problem. We have determined that the translational and rotational velocities of the squirmer are independent of the linear shear flow induced by the background flow. However, the linear shear-flow plays a role in the velocity field generated by the squirmer.
$U_s=2(1+U_p)/3$ only depends on the first swimming mode (as it does for propulsion in uniform flows first reported by Lighthill Reference Lighthill1952; Blake Reference Blake1971), it is now influenced by the strength of the background flow. The dependence on the maximum velocity of the paraboloidal flow played a significant role in the amount of work being experienced by the squirmer. However, although we have determined the range of flow strength that minimises work, we have shown that squirmers in paraboloidal flows are always more efficient compared with squirmers in uniform flows. We then considered the more general, non-axisymmetric problem of a squirmer off the centreline of the background flow. In this framework, the shear-induced orientation and rotation of the squirmer now enter the problem. We have determined that the translational and rotational velocities of the squirmer are independent of the linear shear flow induced by the background flow. However, the linear shear-flow plays a role in the velocity field generated by the squirmer.
Since paraboloidal flows are a critical component of Poiseuille flow, our findings provide metrics for future studies of microswimming in this biologically relevant non-uniform flow. Specifically, critical questions to be addressed include: How will propulsion in complex fluids compare with locomotion in Newtonian fluids? What gains in performance metrics will particle geometry yield compared with spherical swimmers? How will swimming with a cage (Reigh & Lauga Reference Reigh and Lauga2017; Reigh et al. Reference Reigh, Zhu, Gallaire and Lauga2017) be affected in a paraboloidal flow? Our results also have significant implications on various biological processes that depend on the flow fields generated by microswimmers, including feeding (Magar, Goto & Pedley Reference Magar, Goto and Pedley2003; Ishikawa et al. Reference Ishikawa, Kajiki, Imai and Omori2016; Gilpin et al. Reference Gilpin, Prakash and Prakash2017) and hydrodynamic interactions (Jabbarzadeh & Fu Reference Jabbarzadeh and Fu2018).
Funding
H.N. gratefully acknowledges funding support from the National Science Foundation grant no. 2211633, and from a Jess and Mildred Fisher Endowed Professor of Mathematics from the Fisher College of Science and Mathematics at Towson University. H.N. and D.P. thank the anonymous reviewers who provided pertinent suggestions and comments on our submission.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Paraboloidal background flow
Here we outline the derivation of the paraboloidal background flow in (2.7). Using the stream function formulation ![]() $\psi _\infty = U_p r^4\sin ^4\theta /4$, the background velocity is given by
$\psi _\infty = U_p r^4\sin ^4\theta /4$, the background velocity is given by
The Legendre and associated Legendre polynomials
 \begin{equation} \left.\begin{gathered} P_1 = \cos\theta ,\\ P_2 = \tfrac{1}{2}\left(3\cos^2\theta-1\right), \\ P_3 = \tfrac{1}{2}\left(5\cos^3\theta-3\cos\theta\right) ,\\ P^1_1 ={-}\sin\theta, \\ P^1_2 ={-}3\cos\theta\sin\theta ,\\ P^1_3 ={-}6\sin\theta + \tfrac{15}{2}\sin^3\theta ,\\ P^2_2 = 3\sin^2\theta. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} P_1 = \cos\theta ,\\ P_2 = \tfrac{1}{2}\left(3\cos^2\theta-1\right), \\ P_3 = \tfrac{1}{2}\left(5\cos^3\theta-3\cos\theta\right) ,\\ P^1_1 ={-}\sin\theta, \\ P^1_2 ={-}3\cos\theta\sin\theta ,\\ P^1_3 ={-}6\sin\theta + \tfrac{15}{2}\sin^3\theta ,\\ P^2_2 = 3\sin^2\theta. \end{gathered}\right\} \end{equation}
After some algebraic manipulations, ![]() $P_3$ is used to obtain
$P_3$ is used to obtain ![]() $\cos \theta \sin ^2\theta = 2(P_1-P_3)/5$. Similarly,
$\cos \theta \sin ^2\theta = 2(P_1-P_3)/5$. Similarly, ![]() $P^1_3$ is used to obtain
$P^1_3$ is used to obtain ![]() $\sin ^3\theta = 2(P^1_3-6P^1_1)/15$. Substituting
$\sin ^3\theta = 2(P^1_3-6P^1_1)/15$. Substituting ![]() $\cos \theta \sin ^2\theta$ and
$\cos \theta \sin ^2\theta$ and ![]() $\sin ^3\theta$ into (A1) yields
$\sin ^3\theta$ into (A1) yields
For completeness, we provide the derivatives of the Legendre and associated Legendre polynomials. Note that the derivatives are obtained with respect ![]() $x$, where
$x$, where ![]() $P^m_n\equiv P^m_n(x)$, followed by the substitution
$P^m_n\equiv P^m_n(x)$, followed by the substitution ![]() $x=\cos \theta$:
$x=\cos \theta$:
 \begin{equation} \left.\begin{gathered} P_1' = 1 ,\\ P_2' = 3\cos\theta ,\\ P_3' = \tfrac{3}{2}\left(5\cos^2\theta-1\right) ,\\ P^{1'}_1 = \dfrac{\cos\theta}{\sin\theta}, \\ P^{1'}_2 = \dfrac{3\cos^2\theta}{\sin\theta} - 3\sin\theta ,\\ P^{2'}_2 ={-}6\cos\theta. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} P_1' = 1 ,\\ P_2' = 3\cos\theta ,\\ P_3' = \tfrac{3}{2}\left(5\cos^2\theta-1\right) ,\\ P^{1'}_1 = \dfrac{\cos\theta}{\sin\theta}, \\ P^{1'}_2 = \dfrac{3\cos^2\theta}{\sin\theta} - 3\sin\theta ,\\ P^{2'}_2 ={-}6\cos\theta. \end{gathered}\right\} \end{equation}Appendix B. Validation using PINNs
To validate our analytical results, we simulate the propulsion of a pusher with ![]() $\beta _2=-1$ using a PINN. The problem is implemented in DeepXDE (a Python library for scientific machine learning Lu et al. Reference Lu, Meng, Mao and Karniadakis2021) with a Tensorflow backend (Abadi et al. Reference Abadi2015). We employ a feed-forward neural network consisting of an input layer with two nodes, three hidden layers with 100 nodes per layer and an output layer with three nodes. We use the Adam optimiser and the hyperbolic tangent as the activation function. The learning rate is gradually lowered using a learning rate scheduler, from an initial value of
$\beta _2=-1$ using a PINN. The problem is implemented in DeepXDE (a Python library for scientific machine learning Lu et al. Reference Lu, Meng, Mao and Karniadakis2021) with a Tensorflow backend (Abadi et al. Reference Abadi2015). We employ a feed-forward neural network consisting of an input layer with two nodes, three hidden layers with 100 nodes per layer and an output layer with three nodes. We use the Adam optimiser and the hyperbolic tangent as the activation function. The learning rate is gradually lowered using a learning rate scheduler, from an initial value of ![]() $\nu =3\times 10^{-3}$. A total of 1000 and 300 training points were used inside the computational domain and on the domain's boundaries, respectively. We perform the computations in the domain
$\nu =3\times 10^{-3}$. A total of 1000 and 300 training points were used inside the computational domain and on the domain's boundaries, respectively. We perform the computations in the domain ![]() $[r,\theta ]=[1,10]\times [0,{\rm \pi} ]$. Figure 7 shows comparisons of the velocity magnitude
$[r,\theta ]=[1,10]\times [0,{\rm \pi} ]$. Figure 7 shows comparisons of the velocity magnitude ![]() $\|\boldsymbol {u}\| = \sqrt {u_r^2+u_\theta ^2}$ as a function of the radius for the flow in the back (
$\|\boldsymbol {u}\| = \sqrt {u_r^2+u_\theta ^2}$ as a function of the radius for the flow in the back (![]() $\theta ={\rm \pi}$, figure 7a) and side (
$\theta ={\rm \pi}$, figure 7a) and side (![]() $\theta ={\rm \pi} /2$, figure 7b) of a pusher (
$\theta ={\rm \pi} /2$, figure 7b) of a pusher (![]() $\beta _2=-1$). In both panels, the simulations show good agreement with the analytical solution. The convergence of the PINN simulations towards the propulsion speed is shown in figure 7(c) as a function of the number of iterations for various values of the strength of the background paraboloidal flow.
$\beta _2=-1$). In both panels, the simulations show good agreement with the analytical solution. The convergence of the PINN simulations towards the propulsion speed is shown in figure 7(c) as a function of the number of iterations for various values of the strength of the background paraboloidal flow.

Figure 7. (a,b) Magnitude of the axisymmetric velocity ![]() $\|\boldsymbol {u}\| = \sqrt {u_r^2+u_\theta ^2}$ as a function of the radius
$\|\boldsymbol {u}\| = \sqrt {u_r^2+u_\theta ^2}$ as a function of the radius ![]() $r$ for a pusher with
$r$ for a pusher with ![]() $\beta _2=-1$. The flow decay is shown at the back of the squirmer
$\beta _2=-1$. The flow decay is shown at the back of the squirmer ![]() $\theta ={\rm \pi}$ (a) and at the side of the swimmer
$\theta ={\rm \pi}$ (a) and at the side of the swimmer ![]() $\theta ={\rm \pi} /2$ (b). In (c), the convergence of the propulsion speed predicted by the PINN simulations is shown as a function of the number of iterations. The curves are colour-coded to denote different values of the paraboloidal flow's strength
$\theta ={\rm \pi} /2$ (b). In (c), the convergence of the propulsion speed predicted by the PINN simulations is shown as a function of the number of iterations. The curves are colour-coded to denote different values of the paraboloidal flow's strength ![]() $U_p$. The dash-dotted horizontal lines represent the value of the exact propulsion speed, obtained from (2.12).
$U_p$. The dash-dotted horizontal lines represent the value of the exact propulsion speed, obtained from (2.12).
Appendix C. Derivation of the coefficients in the velocity field
Here we provide an outline of the derivation of the coefficients in the velocity field of the general squirming motion. Lamb's general solution for three-dimensional exterior problems, which satisfies (3.4), is given by (Pak & Lauga Reference Pak and Lauga2014)
 \begin{align} u_r &= \sum^\infty_{n=1} \sum^n_{m=0} \frac{(n+1) P^m_n}{2(2n-1)\mu r^{n+2}}\left\{ \left[ D_{mn}r^2 - 2E_{mn}(2n-1)\mu\right]\cos m\phi \right. \nonumber\\ &\quad \left. + \left[ \hat{D}_{mn}r^2 - 2\hat{E}_{mn}(2n-1)\mu\right]\sin m\phi \right\} \end{align}
\begin{align} u_r &= \sum^\infty_{n=1} \sum^n_{m=0} \frac{(n+1) P^m_n}{2(2n-1)\mu r^{n+2}}\left\{ \left[ D_{mn}r^2 - 2E_{mn}(2n-1)\mu\right]\cos m\phi \right. \nonumber\\ &\quad \left. + \left[ \hat{D}_{mn}r^2 - 2\hat{E}_{mn}(2n-1)\mu\right]\sin m\phi \right\} \end{align} \begin{align} u_\theta &= \sum^\infty_{n=1} \sum^n_{m=0} \frac{1}{2r^n\sin\theta} \left\{ \sin^2\theta P^{m'}_n \left[ \frac{n-2}{n(2n-1)\mu} \left( D_{mn}\cos m\phi + \hat{D}_{mn} \sin m\phi \right) \right. \right. \nonumber\\ &\quad -\left. \left.\frac{2}{r^2}\left( E_{mn}\cos m\phi + \hat{E}_{mn} \sin m\phi \right) \right] + \frac{2m}{r}P^m_n \left( \hat{F}_{mn}\cos m\phi - F_{mn} \sin m\phi \right) \right\} \end{align}
\begin{align} u_\theta &= \sum^\infty_{n=1} \sum^n_{m=0} \frac{1}{2r^n\sin\theta} \left\{ \sin^2\theta P^{m'}_n \left[ \frac{n-2}{n(2n-1)\mu} \left( D_{mn}\cos m\phi + \hat{D}_{mn} \sin m\phi \right) \right. \right. \nonumber\\ &\quad -\left. \left.\frac{2}{r^2}\left( E_{mn}\cos m\phi + \hat{E}_{mn} \sin m\phi \right) \right] + \frac{2m}{r}P^m_n \left( \hat{F}_{mn}\cos m\phi - F_{mn} \sin m\phi \right) \right\} \end{align} \begin{align} u_\phi &= \sum^\infty_{n=1} \sum^n_{m=0} \frac{1}{2r^n\sin\theta} \left\{ m P^{m}_n \left[ \frac{n-2}{n(2n-1)\mu} \left( -\hat{D}_{mn}\cos m\phi + D_{mn} \sin m\phi \right) \right. \right. \nonumber\\ &\quad -\left. \left.\frac{2}{r^2}\left( -\hat{E}_{mn}\cos m\phi + E_{mn} \sin m\phi \right) \right] + \frac{2}{r}\sin^2\theta P^{m'}_n \left( F_{mn}\cos m\phi + \hat{F}_{mn} \sin m\phi \right) \right\} . \end{align}
\begin{align} u_\phi &= \sum^\infty_{n=1} \sum^n_{m=0} \frac{1}{2r^n\sin\theta} \left\{ m P^{m}_n \left[ \frac{n-2}{n(2n-1)\mu} \left( -\hat{D}_{mn}\cos m\phi + D_{mn} \sin m\phi \right) \right. \right. \nonumber\\ &\quad -\left. \left.\frac{2}{r^2}\left( -\hat{E}_{mn}\cos m\phi + E_{mn} \sin m\phi \right) \right] + \frac{2}{r}\sin^2\theta P^{m'}_n \left( F_{mn}\cos m\phi + \hat{F}_{mn} \sin m\phi \right) \right\} . \end{align}
Translation and rotation can occur in any of the ![]() $\boldsymbol {e}_x$,
$\boldsymbol {e}_x$, ![]() $\boldsymbol {e}_y$ and
$\boldsymbol {e}_y$ and ![]() $\boldsymbol {e}_z$, where
$\boldsymbol {e}_z$, where
 \begin{equation} \left.\begin{gathered} \boldsymbol{e}_x=\sin\theta\cos\phi\boldsymbol{e}_r + \cos\theta\cos\phi\boldsymbol{e}_\theta-\sin\phi\boldsymbol{e}_\phi, \\ \boldsymbol{e}_y=\sin\theta\sin\phi\boldsymbol{e}_r + \cos\theta\sin\phi\boldsymbol{e}_\theta+\cos\phi\boldsymbol{e}_\phi, \\ \boldsymbol{e}_z=\cos\theta\boldsymbol{e}_r-\sin\theta\boldsymbol{e}_\theta. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \boldsymbol{e}_x=\sin\theta\cos\phi\boldsymbol{e}_r + \cos\theta\cos\phi\boldsymbol{e}_\theta-\sin\phi\boldsymbol{e}_\phi, \\ \boldsymbol{e}_y=\sin\theta\sin\phi\boldsymbol{e}_r + \cos\theta\sin\phi\boldsymbol{e}_\theta+\cos\phi\boldsymbol{e}_\phi, \\ \boldsymbol{e}_z=\cos\theta\boldsymbol{e}_r-\sin\theta\boldsymbol{e}_\theta. \end{gathered}\right\} \end{equation}
These unit vectors suggest that the velocity fields in these directions will differ only for indices ![]() $mn=01$,
$mn=01$, ![]() $11$ whereas the linear shear flow involves index
$11$ whereas the linear shear flow involves index ![]() $12$. The corresponding flow field and pressure for a three-mode squirmer are given by
$12$. The corresponding flow field and pressure for a three-mode squirmer are given by
 \begin{align} u_r &= \frac{1}{\mu r^3}\left\{ P_1 \left( D_{01}r^2-2E_{01}\mu\right) \right.\nonumber\\ &\quad +\left. P^1_1 \left[ \left(D_{11}r^2-2E_{11}\mu\right) \cos\phi+\left(\hat{D}_{11}r^2-2\hat{E}_{11}\mu\right)\sin\phi\right]\right\} \nonumber\\ &\quad + \frac{1}{2\mu r^4}\left\{ P_2 \left( D_{02}r^2-6E_{02}\mu\right) \right. \nonumber\\ &\quad +\left. P^1_2 \left[ \left(D_{12}r^2-6E_{12}\mu\right)\cos\phi+\left(\hat{D}_{12}r^2-6\hat{E}_{12}\mu\right)\sin\phi\right] \right. \nonumber\\ &\quad +\left. P^2_2 \left[ \left(D_{22}r^2-6E_{22}\mu\right)\cos2\phi+\left(\hat{D}_{22}r^2-6\hat{E}_{22}\mu\right)\sin2\phi\right] \right\} \nonumber\\ &\quad + \frac{2}{5\mu r^5} P_3 \left( D_{03}r^2-10E_{03}\mu\right), \end{align}
\begin{align} u_r &= \frac{1}{\mu r^3}\left\{ P_1 \left( D_{01}r^2-2E_{01}\mu\right) \right.\nonumber\\ &\quad +\left. P^1_1 \left[ \left(D_{11}r^2-2E_{11}\mu\right) \cos\phi+\left(\hat{D}_{11}r^2-2\hat{E}_{11}\mu\right)\sin\phi\right]\right\} \nonumber\\ &\quad + \frac{1}{2\mu r^4}\left\{ P_2 \left( D_{02}r^2-6E_{02}\mu\right) \right. \nonumber\\ &\quad +\left. P^1_2 \left[ \left(D_{12}r^2-6E_{12}\mu\right)\cos\phi+\left(\hat{D}_{12}r^2-6\hat{E}_{12}\mu\right)\sin\phi\right] \right. \nonumber\\ &\quad +\left. P^2_2 \left[ \left(D_{22}r^2-6E_{22}\mu\right)\cos2\phi+\left(\hat{D}_{22}r^2-6\hat{E}_{22}\mu\right)\sin2\phi\right] \right\} \nonumber\\ &\quad + \frac{2}{5\mu r^5} P_3 \left( D_{03}r^2-10E_{03}\mu\right), \end{align} \begin{align} u_\theta &= \frac{1}{2r\sin\theta} \left\{ \sin^2\theta P_1'\left(-\frac{1}{\mu}D_{01}-\frac{2}{r^2}E_{01}\right) \right. \nonumber\\ &\quad +\left. \sin^2\theta P^{1'}_1\left[ -\frac{1}{\mu}\left(D_{11}\cos\phi+\hat{D}_{11}\sin\phi\right) - \frac{2}{r^2}\left(E_{11}\cos\phi+\hat{E}_{11}\sin\phi\right) \right] \right. \nonumber\\ &\quad +\left. \frac{2}{r}P^1_1\left(\hat{F}_{11}\cos\phi-F_{11}\sin\phi\right) \right\} + \frac{1}{2r^2\sin\theta} \left\{ -\frac{2\sin^2\theta P_2'}{r^2}E_{02} \right. \nonumber\\ &\quad -\left.\frac{2\sin^2\theta P^{1'}_2}{r^2}\left(E_{12}\cos\phi+\hat{E}_{12}\sin\phi\right) + \frac{2}{r}P^1_2\left(\hat{F}_{12}\cos\phi-F_{12}\sin\phi\right) \right. \nonumber\\ &\quad -\left.\frac{2\sin^2\theta P^{2'}_2}{r^2}\left(E_{22}\cos2\phi+\hat{E}_{22}\sin2\phi\right) + \frac{4}{r}P^2_2\left(\hat{F}_{22}\cos2\phi-F_{22}\sin2\phi\right) \right\} \nonumber\\ &\quad + \frac{1}{2r^3\sin\theta} \sin^2\theta P_3' \left(\frac{1}{15\mu}D_{03}-\frac{2}{r^2}E_{03} \right), \end{align}
\begin{align} u_\theta &= \frac{1}{2r\sin\theta} \left\{ \sin^2\theta P_1'\left(-\frac{1}{\mu}D_{01}-\frac{2}{r^2}E_{01}\right) \right. \nonumber\\ &\quad +\left. \sin^2\theta P^{1'}_1\left[ -\frac{1}{\mu}\left(D_{11}\cos\phi+\hat{D}_{11}\sin\phi\right) - \frac{2}{r^2}\left(E_{11}\cos\phi+\hat{E}_{11}\sin\phi\right) \right] \right. \nonumber\\ &\quad +\left. \frac{2}{r}P^1_1\left(\hat{F}_{11}\cos\phi-F_{11}\sin\phi\right) \right\} + \frac{1}{2r^2\sin\theta} \left\{ -\frac{2\sin^2\theta P_2'}{r^2}E_{02} \right. \nonumber\\ &\quad -\left.\frac{2\sin^2\theta P^{1'}_2}{r^2}\left(E_{12}\cos\phi+\hat{E}_{12}\sin\phi\right) + \frac{2}{r}P^1_2\left(\hat{F}_{12}\cos\phi-F_{12}\sin\phi\right) \right. \nonumber\\ &\quad -\left.\frac{2\sin^2\theta P^{2'}_2}{r^2}\left(E_{22}\cos2\phi+\hat{E}_{22}\sin2\phi\right) + \frac{4}{r}P^2_2\left(\hat{F}_{22}\cos2\phi-F_{22}\sin2\phi\right) \right\} \nonumber\\ &\quad + \frac{1}{2r^3\sin\theta} \sin^2\theta P_3' \left(\frac{1}{15\mu}D_{03}-\frac{2}{r^2}E_{03} \right), \end{align} \begin{align} u_\phi &= \frac{1}{2r\sin\theta}\left\{ \frac{2 \sin^2\theta P_1' }{r} F_{01} \right. \nonumber\\ &\quad +\left. P^1_1\left[ -\frac{1}{\mu}\left(-\hat{D}_{11}\cos\phi+D_{11}\sin\phi\right) - \frac{2}{r^2}\left(-\hat{E}_{11}\cos\phi+E_{11}\sin\phi\right) \right] \right. \nonumber\\ &\quad +\left. \frac{2\sin^2\theta P^{1'}_1}{r^2}\left(F_{11}\cos\phi+\hat{F}_{11}\sin\phi\right) \right\} + \frac{1}{2r^2\sin\theta} \left\{ \frac{2\sin^2\theta P_2'}{r} F_{02} \right. \nonumber\\ &\quad -\left. \frac{2P^1_2}{r^2}\left(-\hat{E}_{12}\cos\phi+E_{12}\sin\phi\right) + \frac{2\sin^2\theta P^{1'}_2}{r}\left(F_{12}\cos\phi+\hat{F}_{12}\sin\phi\right) \right. \nonumber\\ &\quad -\left. \frac{4P^2_2}{r^2}\left(-\hat{E}_{22}\cos2\phi+E_{22}\sin2\phi\right) + \frac{2\sin^2\theta P^{2'}_2}{r}\left(F_{22}\cos2\phi+\hat{F}_{22}\sin2\phi\right) \right\} \nonumber\\ &\quad + \frac{1}{2r^3\sin\theta} \frac{2\sin^2\theta P_3'}{r} F_{03}, \end{align}
\begin{align} u_\phi &= \frac{1}{2r\sin\theta}\left\{ \frac{2 \sin^2\theta P_1' }{r} F_{01} \right. \nonumber\\ &\quad +\left. P^1_1\left[ -\frac{1}{\mu}\left(-\hat{D}_{11}\cos\phi+D_{11}\sin\phi\right) - \frac{2}{r^2}\left(-\hat{E}_{11}\cos\phi+E_{11}\sin\phi\right) \right] \right. \nonumber\\ &\quad +\left. \frac{2\sin^2\theta P^{1'}_1}{r^2}\left(F_{11}\cos\phi+\hat{F}_{11}\sin\phi\right) \right\} + \frac{1}{2r^2\sin\theta} \left\{ \frac{2\sin^2\theta P_2'}{r} F_{02} \right. \nonumber\\ &\quad -\left. \frac{2P^1_2}{r^2}\left(-\hat{E}_{12}\cos\phi+E_{12}\sin\phi\right) + \frac{2\sin^2\theta P^{1'}_2}{r}\left(F_{12}\cos\phi+\hat{F}_{12}\sin\phi\right) \right. \nonumber\\ &\quad -\left. \frac{4P^2_2}{r^2}\left(-\hat{E}_{22}\cos2\phi+E_{22}\sin2\phi\right) + \frac{2\sin^2\theta P^{2'}_2}{r}\left(F_{22}\cos2\phi+\hat{F}_{22}\sin2\phi\right) \right\} \nonumber\\ &\quad + \frac{1}{2r^3\sin\theta} \frac{2\sin^2\theta P_3'}{r} F_{03}, \end{align}and
 \begin{align} p &= \frac{1}{8 \mu r^5} \left\{r \cot \theta \left(\sin \theta \left(8 D_{01} r^2+3 D_{03}\right)-2 \cos \phi (3D_{12} r+4 \hat{F}_{11} \mu (2 r-1)) \right. \right. \nonumber\\ &\left. \left.\quad -\,2 \sin \phi (3 \hat{D}_{12} r+4 F_{11} \mu -8 F_{11} \mu r)\right)+r \left(6 D_{02} r \cos 2 \theta \right. \right. \nonumber\\ &\left. \left.\quad+\,\cos 3 \theta \csc \theta (5 D_{03} \sin \theta +6 D_{12} r \cos \phi+6 \hat{D}_{12} r \sin \phi \right. \right. \nonumber\\ &\left. \left.\quad -\,8 F_{11} \mu \sin \phi +8 \hat{F}_{11} \mu \cos \phi )-8 r \sin \theta (D_{11} r \cos \phi +\hat{D}_{11} r \sin \phi \right. \right. \nonumber\\ &\left. \left.\quad +\,3 D_{22} \sin \theta \cos 2 \phi)\right) +2 D_{02} r^2 +12 \sin 2 \phi \left(\cos 2 \theta \left(\hat{D}_{22} r^2+4 \hat{E}_{12} \mu +5 \hat{E}_{22} \mu \right) \right. \right. \nonumber\\ &\left. \left.\quad -\,\hat{D}_{22} r^2+4 \hat{E}_{12} \mu +3 \hat{E}_{22} \mu \right) \right\}. \end{align}
\begin{align} p &= \frac{1}{8 \mu r^5} \left\{r \cot \theta \left(\sin \theta \left(8 D_{01} r^2+3 D_{03}\right)-2 \cos \phi (3D_{12} r+4 \hat{F}_{11} \mu (2 r-1)) \right. \right. \nonumber\\ &\left. \left.\quad -\,2 \sin \phi (3 \hat{D}_{12} r+4 F_{11} \mu -8 F_{11} \mu r)\right)+r \left(6 D_{02} r \cos 2 \theta \right. \right. \nonumber\\ &\left. \left.\quad+\,\cos 3 \theta \csc \theta (5 D_{03} \sin \theta +6 D_{12} r \cos \phi+6 \hat{D}_{12} r \sin \phi \right. \right. \nonumber\\ &\left. \left.\quad -\,8 F_{11} \mu \sin \phi +8 \hat{F}_{11} \mu \cos \phi )-8 r \sin \theta (D_{11} r \cos \phi +\hat{D}_{11} r \sin \phi \right. \right. \nonumber\\ &\left. \left.\quad +\,3 D_{22} \sin \theta \cos 2 \phi)\right) +2 D_{02} r^2 +12 \sin 2 \phi \left(\cos 2 \theta \left(\hat{D}_{22} r^2+4 \hat{E}_{12} \mu +5 \hat{E}_{22} \mu \right) \right. \right. \nonumber\\ &\left. \left.\quad -\,\hat{D}_{22} r^2+4 \hat{E}_{12} \mu +3 \hat{E}_{22} \mu \right) \right\}. \end{align}
The unknown coefficients ![]() $D_{mn},\hat {D}_{mn},E_{mn},\hat {E}_{mn},F_{mn},\hat {F}_{mn}$ are obtained by satisfying the boundary condition given by (3.3) and are provided in tables 1 and 2. The coefficients
$D_{mn},\hat {D}_{mn},E_{mn},\hat {E}_{mn},F_{mn},\hat {F}_{mn}$ are obtained by satisfying the boundary condition given by (3.3) and are provided in tables 1 and 2. The coefficients ![]() $\triangledown$,
$\triangledown$, ![]() $\triangledown ^*$,
$\triangledown ^*$, ![]() $\triangle$,
$\triangle$, ![]() $\triangle^*$ in table 1 are given by
$\triangle^*$ in table 1 are given by
Table 1. Coefficients of the flow field for ![]() $m=0$. The
$m=0$. The ![]() $-$ denotes a coefficient that remains the same across directions. The coefficients represented by
$-$ denotes a coefficient that remains the same across directions. The coefficients represented by ![]() $\triangledown,\bigtriangledown ^*,\triangle,\triangle ^*$ are expressed in terms of the translational velocity and/or maximum velocity of the background flow ((C9)–(C11a,b)).
$\triangledown,\bigtriangledown ^*,\triangle,\triangle ^*$ are expressed in terms of the translational velocity and/or maximum velocity of the background flow ((C9)–(C11a,b)).

Table 2. Coefficients of the flow field for ![]() $m=1$. The
$m=1$. The ![]() $-$ denotes a coefficient that remains the same across directions.
$-$ denotes a coefficient that remains the same across directions.

The translational and rotational velocities are obtained from the force- and torque-free conditions along each direction. Specifically, in spherical coordinates, the force- and torque-free conditions in the ![]() $\boldsymbol {e}_x$ direction are
$\boldsymbol {e}_x$ direction are
the force- and torque-free conditions in the ![]() $\boldsymbol {e}_y$ direction are
$\boldsymbol {e}_y$ direction are
and the force- and torque-free conditions in the ![]() $\boldsymbol {e}_z$ direction are
$\boldsymbol {e}_z$ direction are