Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T08:15:01.698Z Has data issue: false hasContentIssue false
  • English
  • Français

Circulation conservation and vortex breakup in magnetohydrodynamics at low magnetic Prandtl number

Published online by Cambridge University Press:  15 October 2018

D. G. Dritschel Open the ORCID record for D. G. Dritschel [Opens in a new window] ,
P. H. Diamond  and
S. M. Tobias
D. G. Dritschel
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
P. H. Diamond
Affiliation:
Center for Astrophysics and Space Sciences, University of California, San Diego, La Jolla, CA 92093, USA Department of Physics, University of California, San Diego, La Jolla, CA 92093, USA Center for Fusion Sciences, Southwestern Institute of Physics, Chengdu, Sichuan 610041, PR China
S. M. Tobias*
Affiliation:
Department of Applied Mathematics, University of Leeds, Leeds LS2 9JT, UK
*
†Email address for correspondence: smt@maths.leeds.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we examine the role of weak magnetic fields in breaking Kelvin’s circulation theorem and in vortex breakup in two-dimensional magnetohydrodynamics for the physically important case of a fluid with low magnetic Prandtl number (low 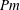$Pm$). We consider three canonical inviscid solutions for the purely hydrodynamical problem, namely a Gaussian vortex, a circular vortex patch and an elliptical vortex patch. We examine how magnetic fields lead to an initial loss of circulation 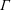$\unicode[STIX]{x1D6E4}$ and attempt to derive scaling laws for the loss of circulation as a function of field strength and diffusion as measured by two non-dimensional parameters. We show that for all cases the loss of circulation depends on the integrated effects of the Lorentz force, with the patch cases leading to significantly greater circulation loss. For the case of the elliptical vortex, the loss of circulation depends on the total area swept out by the rotating vortex, and so this leads to more efficient circulation loss than for a circular vortex.

JFM classification

Vortex Flows: Contour dynamics MHD and Electrohydrodynamics: MHD and Electrohydrodynamics Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 857 , 25 December 2018 , pp. 38 - 60
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bajer, K., Bassom, A. P. & Gilbert, A. D. 2001 Accelerated diffusion in the centre of a vortex. J. Fluid Mech. 437, 395–411.Google Scholar
Banerjee, D. & Pandit, R. 2014 Statistics of the inverse-cascade regime in two-dimensional magnetohydrodynamic turbulence. Phys. Rev. E 90 (1), 013018.Google Scholar
Baty, H. & Keppens, R. 2002 Interplay between Kelvin–Helmholtz and current-driven instabilities in jets. Astrophys. J. 580, 800–814.Google Scholar
Buffett, B. 2014 Geomagnetic fluctuations reveal stable stratification at the top of the Earth’s core. Nature 507, 484–487.Google Scholar
Cao, C., Wu, J. & Yuan, B.2017 The 2D incompressible magnetohydrodynamics equations with only magnetic diffusion. arXiv:1306.3629 [math.AP].Google Scholar
Cattaneo, F. 1994 On the effects of a weak magnetic field on turbulent transport. Astrophys. J. 434, 200–205.Google Scholar
Cattaneo, F. & Vainshtein, S. I. 1991 Suppression of turbulent transport by a weak magnetic field. Astrophys. J. Lett. 376, L21–L24.Google Scholar
Christensen, U. R. & Wicht, J. 2008 Models of magnetic field generation in partly stable planetary cores: applications to Mercury and Saturn. Icarus 196, 16–34.Google Scholar
Dormy, E. & Soward, A. M. 2007 Mathematical Aspects of Natural Dynamos. CRC Press/Taylor & Francis.Google Scholar
Dritschel, D. G. & Fontane, J. 2010 The combined Lagrangian advection method. J. Comput. Phys. 229, 5408–5417.Google Scholar
Dritschel, D. G. & McIntyre, M. E. 2008 Multiple jets as PV staircases: the Phillips effect and the resilience of eddy-transport barriers. J. Atmos. Sci. 65, 855–874.Google Scholar
Dritschel, D. G. & Tobias, S. M. 2012 Two-dimensional magnetohydrodynamic turbulence in the small magnetic Prandtl number limit. J. Fluid Mech. 703, 85–98.Google Scholar
Frank, A., Jones, T. W., Ryu, D. & Gaalaas, J. B. 1996 The magnetohydrodynamic Kelvin–Helmholtz instability: a two-dimensional numerical study. Astrophys. J. 460, 777–793.Google Scholar
Gilbert, A. D., Mason, J. & Tobias, S. M. 2016 Flux expulsion with dynamics. J. Fluid Mech. 791, 568–588.Google Scholar
Gilman, P. A. 2000 Magnetohydrodynamic ‘shallow water’ equations for the solar tachocline. Astrophys. J. Lett. 544, L79–L82.Google Scholar
Gruzinov, A. V. & Diamond, P. H. 1994 Self-consistent theory of mean-field electrodynamics. Phys. Rev. Lett. 72 (11), 1651–1653.Google Scholar
Gubbins, D. & Davies, C. J. 2013 The stratified layer at the core–mantle boundary caused by barodiffusion of oxygen, sulphur and silicon. Phys. Earth Planet. Inter. 215, 21–28.Google Scholar
Hughes, D. W., Rosner, R. & Weiss, N. O. 2012 The Solar Tachocline. Cambridge University Press.Google Scholar
Jones, T. W., Gaalaas, J. B., Ryu, D. & Frank, A. 1997 The MHD Kelvin–Helmholtz instability. II. The roles of weak and oblique fields in planar flows. Astrophys. J. 482, 230–244.Google Scholar
Keating, S. R., Silvers, L. J. & Diamond, P. H. 2008 On cross-phase and the quenching of the turbulent diffusion of magnetic fields in two dimensions. Astrophys. J. 678 (2), L137–L140.Google Scholar
Kondić, T., Hughes, D. W. & Tobias, S. M. 2016 The decay of a weak large-scale magnetic field in two-dimensional turbulence. Astrophys. J. 823, 111.Google Scholar
Love, A. E. H. 1893 On the stability of certain vortex motions. Proc. Lond. Math. Soc. 35, 18.Google Scholar
Mak, J., Griffiths, S. D. & Hughes, D. W. 2017 Vortex disruption by magnetohydrodynamic feedback. Phys. Rev. Fluids 2, 113701.Google Scholar
Miesch, M. S. & Gilman, P. A. 2004 Thin-shell magnetohydrodynamic equations for the solar tachocline. Solar Phys. 220, 287–305.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. p. 353. Cambridge University Press.Google Scholar
Moffatt, H. K. 1983 Transport effects associated with turbulence with particular attention to the influence of helicity. Rep. Prog. Phys. 46, 621–623.Google Scholar
Moffatt, H. K. & Kamkar, H. 1983 The time-scale associated with flux expulsion. In Stellar and Planetary Magnetism. Proceedings of the Workshop Held 25–29 August 1980, Budapest, Hungary (ed. Soward, A. M.), p. 91. Gordon and Breach Science Publishers.Google Scholar
Palotti, M. L., Heitsch, F., Zweibel, E. G. & Huang, Y.-M. 2008 Evolution of unmagnetized and magnetized shear layers. Astrophys. J. 678, 234–244.Google Scholar
Pouquet, A. 1978 On two-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 88, 1–16.Google Scholar
Rüdiger, G., Kitchatinov, L. L. & Hollerbach, R. 2013 Magnetic Processes in Astrophysics: Theory, Simulations, Experiments. Wiley.Google Scholar
Seshasayanan, K. & Alexakis, A. 2016 Critical behavior in the inverse to forward energy transition in two-dimensional magnetohydrodynamic flow. Phys. Rev. E 93 (1), 013104.Google Scholar
Seshasayanan, K., Benavides, S. J. & Alexakis, A. 2014 On the edge of an inverse cascade. Phys. Rev. E 90 (5), 051003.Google Scholar
Stevenson, D. J. 2003 Planetary magnetic fields. Earth Planet. Sci. Lett. 208, 1–11.Google Scholar
Tobias, S. M. 2005 The solar tachocline: formation, stability and its role in the solar dynamo. In Fluid Dynamics and Dynamos in Astrophysics and Geophysics (ed. Soward, A. M., Jones, C. A., Hughes, D. W. & Weiss, N. O.), pp. 193–233.Google Scholar
Tobias, S. 2010 The solar tachocline: a study in stably stratified MHD turbulence. In IUTAM Symposium on Turbulence in the Atmosphere and Oceans, pp. 169–179. Springer.Google Scholar
Tobias, S. M., Cattaneo, F. & Boldyrev, S. 2013 MHD Dynamos and Turbulence, pp. 351–404.Google Scholar
Tobias, S. M., Diamond, P. H. & Hughes, D. W. 2007 𝛽-plane magnetohydrodynamic turbulence in the solar tachocline. Astrophys. J. Lett. 667, L113–L116.Google Scholar
Weiss, N. O. 1966 The expulsion of magnetic flux by eddies. Proc. R. Soc. Lond. A 293, 310–328.Google Scholar
Weiss, N. O. & Proctor, M. R. E. 2014 Magnetoconvection. Cambridge University Press.Google Scholar