Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T13:49:21.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Closed-loop control of unsteadiness over a rounded backward-facing step

Published online by Cambridge University Press:  12 June 2012

Alexandre Barbagallo ,
Gregory Dergham ,
Denis Sipp ,
Peter J. Schmid  and
Jean-Christophe Robinet
Alexandre Barbagallo
Affiliation:
ONERA – The French Aerospace Lab, 8 rue des Vertugadins, 92190 Meudon, France Laboratoire d’Hydrodynamique (LadHyX), CNRS – Ecole Polytechnique, 91128 Palaiseau, France
Gregory Dergham
Affiliation:
DynFluid Laboratory, Arts et Metiers ParisTech, 151 Boulevard de l’Hôpital, 75013 Paris, France
Denis Sipp
Affiliation:
ONERA – The French Aerospace Lab, 8 rue des Vertugadins, 92190 Meudon, France
Peter J. Schmid*
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), CNRS – Ecole Polytechnique, 91128 Palaiseau, France
Jean-Christophe Robinet
Affiliation:
DynFluid Laboratory, Arts et Metiers ParisTech, 151 Boulevard de l’Hôpital, 75013 Paris, France
*
†Email address for correspondence: peter@ladhyx.polytechnique.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The two-dimensional, incompressible flow over a rounded backward-facing step at Reynolds number 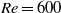is characterized by a detachment of the flow close to the step followed by a recirculation zone. Even though the flow is globally stable, perturbations are amplified as they are convected along the shear layer, and the presence of upstream random noise renders the flow unsteady, leading to a broadband spectrum of excited frequencies. This paper is aimed at suppressing this unsteadiness using a controller that converts a shear-stress measurement taken from a wall-mounted sensor into a control law that is supplied to an actuator. A comprehensive study of various components of closed-loop control design – covering sensor placement, choice and influence of the cost functional, accuracy of the reduced-order model, compensator stability and performance – shows that successful control of this flow requires a judicious balance between estimation speed and estimation accuracy, and between stability limits and performance requirements. The inherent amplification behaviour of the flow can be reduced by an order of magnitude if the above-mentioned constraints are observed. In particular, to achieve superior controller performance, the estimation sensor should be placed upstream near the actuator to ensure sufficient estimation speed. Also, if high-performance compensators are sought, a very accurate reduced-order model is required, especially for the dynamics between the actuator and the estimation sensor; otherwise, very minute errors even at low energies and high frequencies may render the large-scale compensated linearized simulation unstable. Finally, coupling the linear compensator to nonlinear simulations shows a gradual deterioration in control performance as the amplitude of the noise increases.

JFM classification

Boundary Layers: Boundary layer control Flow Control: Control theory Wakes/Jets: Separated flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 703 , 25 July 2012 , pp. 326 - 362
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ahuja, S. & Rowley, C. W. 2010 Feedback control of unstable steady states of flow past a flat plate using reduced-order estimators. J. Fluid Mech. 645, 447–478.CrossRefGoogle Scholar
2. Åkervik, E., Hœpffner, J., Ehrenstein, U. & Henningson, D. S. 2007 Optimal growth, model reduction and control in a separated boundary-layer flow using global modes. J. Fluid Mech. 579, 305–314.CrossRefGoogle Scholar
3. Alizard, F., Cherubini, S. & Robinet, J.-C. 2009 Sensitivity and optimal forcing response in separated boundary layer flows. Phys. Fluids 21, 064108.CrossRefGoogle Scholar
4. Archambaud, J. P., Arnal, D., Hein, S., Melo de Souza, J., Hanifi, A., Goddard, J. L., Krier, J. & Donelli, R. 2008 Use of laminar flow technologies for supersonic drag reduction – results of FP project SUPERTRAC. In Proceedings of the 5th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS), Venice, Italy.Google Scholar
5. Bagheri, S., Brandt, L. & Henningson, D. S. 2009 Input–output analysis, model reduction and control of the flat-plate boundary layer. J. Fluid Mech. 620, 263–298.CrossRefGoogle Scholar
6. Bagheri, S. & Henningson, D. S. 2011 Transition delay using control theory. Phil. Trans. R. Soc. A 369, 1365–1381.CrossRefGoogle ScholarPubMed
7. Barbagallo, A., Sipp, D. & Schmid, P. J. 2009 Closed-loop control of an open cavity flow using reduced-order models. J. Fluid Mech. 641, 1–50.CrossRefGoogle Scholar
8. Bewley, T. R. & Liu, S. 1998 Optimal and robust control and estimation of linear paths to transition. J. Fluid Mech. 365, 305–349.CrossRefGoogle Scholar
9. Blackburn, H. M., Barkley, D. & Sherwin, S. J. 2008 Convective instability and transient growth in flow over a backward-facing step. J. Fluid Mech. 603, 271–304.CrossRefGoogle Scholar
10. Boiko, A. V., Dovgal, A. V. & Hein, S. 2008 Control of a laminar separating boundary layer by induced stationary perturbations. Eur. J. Mech. (B/Fluids) 27 (4), 466–476.CrossRefGoogle Scholar
11. Burl, J. B. 1999 Linear Optimal Control. 𝓗2 and 𝓗∞ Methods. Addison-Wesley.Google Scholar
12. Chevalier, M., Hœpffner, J., Åkervik, E. & Henningson, D. S. 2007 Linear feedback control and estimation applied to instabilities in spatially developing boundary layers. J. Fluid Mech. 588, 163–187.CrossRefGoogle Scholar
13. Dergham, G., Sipp, D., Robinet, J.-C. & Barbagallo, A. 2011 Model reduction for fluids using frequential snapshots. Phys. Fluids 23, 064101.CrossRefGoogle Scholar
14. Doyle, J. 1978 Guaranteed margins for LQG regulators. IEEE Trans. Autom. Control 23 (4), 756–757.CrossRefGoogle Scholar
15. Ehrenstein, U., Passaggia, P.-Y. & Gallaire, F. 2011 Control of a separated boundary layer: reduced-order modeling using global modes revisited. Theor. Comput. Fluid Dyn. 25 (1–4), 195–207.CrossRefGoogle Scholar
16. Gharib, M. & Roshko, A. 1987 The effect of flow oscillations on cavity drag. J. Fluid Mech. 177, 501–530.CrossRefGoogle Scholar
17. Hecht, F., Pironneau, O., Hyaric, A. Le & Ohtsuka, K. 2005 Freefem++, 3rd edition, version 3.19, http://www.freefem.org/ff++, Université Pierre et Marie Curie Paris, Laboratoire Jacques-Louis Lions.Google Scholar
18. Ilak, M. 2009 Model reduction and feedback control of transitional channel flow. PhD thesis, Princeton University, Mechanical and Aerospace Engineering.Google Scholar
19. Ilak, M. & Rowley, C. W. 2008 Modeling of transitional channel flow using balanced proper orthogonal decomposition. Phys. Fluids 20, 034103.CrossRefGoogle Scholar
20. Joshi, S. S., Speyer, J. L. & Kim, J. 1997 A systems theory approach to the feedback stabilization of infinitesimal and finite-amplitude disturbances in plane Poiseuille flow. J. Fluid Mech. 332, 157–184.CrossRefGoogle Scholar
21. Joslin, R. D. 1998 Overview of laminar flow control. NASA Rep. TP 208705.Google Scholar
22. Kim, J. 2003 Control of turbulent boundary layers. Phys. Fluids 15, 1093–1105.CrossRefGoogle Scholar
23. Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.CrossRefGoogle Scholar
24. Marquet, O., Sipp, D., Chomaz, J.-M. & Jacquin, L. 2008 Amplifier and resonator dynamics of a low-Reynolds number recirculation bubble in a global framework. J. Fluid Mech. 605, 429–443.CrossRefGoogle Scholar
25. Rossiter, J. E. 1964 Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds. Aero. Res. Counc. R&M 3438.Google Scholar
26. Rowley, C. W. 2005 Model reduction for fluids using balanced proper orthogonal decomposition. Intl J. Bifurcation Chaos 15, 997–1013.CrossRefGoogle Scholar
27. Saric, W. S., Reed, H. L. & White, E. B. 2003 Stability and transition of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 35, 413–440.CrossRefGoogle Scholar
28. Sipp, D., Marquet, O., Meliga, P. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open flows: a linearized approach. Appl. Mech. Rev. 63, 030801.CrossRefGoogle Scholar
29. Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Q. Appl. Maths 45, 561–590.CrossRefGoogle Scholar

Barbagallo et al. supplementary movie

Animation of control of flow over a backward-facing step

Download Barbagallo et al. supplementary movie(Video)
Video 9.1 MB

Barbagallo et al. supplementary movie

Animation of control of flow over a backward-facing step

Download Barbagallo et al. supplementary movie(Video)
Video 44.9 MB