Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Parezanović, Vladimir
Laurentie, Jean-Charles
Fourment, Carine
Delville, Joël
Bonnet, Jean-Paul
Spohn, Andreas
Duriez, Thomas
Cordier, Laurent
Noack, Bernd R.
Abel, Markus
Segond, Marc
Shaqarin, Tamir
and
Brunton, Steven L.
2015.
Mixing Layer Manipulation Experiment.
Flow, Turbulence and Combustion,
Vol. 94,
Issue. 1,
p.
155.
Brunton, Steven L.
and
Noack, Bernd R.
2015.
Closed-Loop Turbulence Control: Progress and Challenges.
Applied Mechanics Reviews,
Vol. 67,
Issue. 5,
Flores-Fuentes, Wendy
Sergiyenko, Oleg
Gonzalez-Navarro, Félix F.
Rivas-López, Moisés
Rodríguez-Quiñonez, Julio C.
Hernández-Balbuena, Daniel
Tyrsa, Vera
and
Lindner, Lars
2016.
Multivariate outlier mining and regression feedback for 3D measurement improvement in opto-mechanical system.
Optical and Quantum Electronics,
Vol. 48,
Issue. 8,
Parezanović, Vladimir
Cordier, Laurent
Spohn, Andreas
Duriez, Thomas
Noack, Bernd R.
Bonnet, Jean-Paul
Segond, Marc
Abel, Markus
and
Brunton, Steven L.
2016.
Frequency selection by feedback control in a turbulent shear flow.
Journal of Fluid Mechanics,
Vol. 797,
Issue. ,
p.
247.
Benard, N.
Pons-Prats, J.
Periaux, J.
Bugeda, G.
Braud, P.
Bonnet, J. P.
and
Moreau, E.
2016.
Turbulent separated shear flow control by surface plasma actuator: experimental optimization by genetic algorithm approach.
Experiments in Fluids,
Vol. 57,
Issue. 2,
Hack, M. J. Philipp
and
Zaki, Tamer A.
2016.
Data-enabled prediction of streak breakdown in pressure-gradient boundary layers.
Journal of Fluid Mechanics,
Vol. 801,
Issue. ,
p.
43.
Quade, Markus
Abel, Markus
Shafi, Kamran
Niven, Robert K.
and
Noack, Bernd R.
2016.
Prediction of dynamical systems by symbolic regression.
Physical Review E,
Vol. 94,
Issue. 1,
Sipp, Denis
and
Schmid, Peter J.
2016.
Linear Closed-Loop Control of Fluid Instabilities and Noise-Induced Perturbations: A Review of Approaches and Tools1.
Applied Mechanics Reviews,
Vol. 68,
Issue. 2,
Burns, William R.
Jumper, Eric J.
and
Gordeyev, Stanislav
2016.
A Robust Modification of a Predictive Adaptive-Optic Control Method for Aero-Optics.
Lasagna, Davide
Huang, Deqing
Tutty, Owen R.
and
Chernyshenko, Sergei
2016.
Sum-of-squares approach to feedback control of laminar wake flows.
Journal of Fluid Mechanics,
Vol. 809,
Issue. ,
p.
628.
Flinois, Thibault L. B.
and
Morgans, Aimee S.
2016.
Feedback control of unstable flows: a direct modelling approach using the Eigensystem Realisation Algorithm.
Journal of Fluid Mechanics,
Vol. 793,
Issue. ,
p.
41.
Guéniat, Florimond
Mathelin, Lionel
and
Hussaini, M. Yousuff
2016.
A statistical learning strategy for closed-loop control of fluid flows.
Theoretical and Computational Fluid Dynamics,
Vol. 30,
Issue. 6,
p.
497.
Flores-Fuentes, Wendy
Sergiyenko, Oleg
Gonzalez-Navarro, Félix F.
Rivas-López, Moisés
Hernandez-Balbuena, Daniel
Rodríguez-Quiñonez, Julio C.
Tyrsa, Vera
and
Lindner, Lars
2016.
Optoelectronic instrumentation enhancement using data mining feedback for a 3D measurement system.
Optical Review,
Vol. 23,
Issue. 6,
p.
891.
Fadla, F.
Graziani, A.
Kerherve, F.
Mathis, R.
Lippert, M.
Uystepruyst, D.
and
Keirsbulck, L.
2016.
Electrochemical Measurements for Real-Time Stochastic Reconstruction of Large-Scale Dynamics of a Separated Flow.
Journal of Fluids Engineering,
Vol. 138,
Issue. 12,
Brackston, R. D.
García de la Cruz, J. M.
Wynn, A.
Rigas, G.
and
Morrison, J. F.
2016.
Stochastic modelling and feedback control of bistability in a turbulent bluff body wake.
Journal of Fluid Mechanics,
Vol. 802,
Issue. ,
p.
726.
Debien, Antoine
von Krbek, Kai A. F. F.
Mazellier, Nicolas
Duriez, Thomas
Cordier, Laurent
Noack, Bernd R.
Abel, Markus W.
and
Kourta, Azeddine
2016.
Closed-loop separation control over a sharp edge ramp using genetic programming.
Experiments in Fluids,
Vol. 57,
Issue. 3,
Wu, Z.
Zhou, Y.
Cao, H. L.
and
Li, W. J.
2016.
Closed-loop enhancement of jet mixing with extremum-seeking and physics-based strategies.
Experiments in Fluids,
Vol. 57,
Issue. 6,
Gao, Chuanqiang
Zhang, Weiwei
Kou, Jiaqing
Liu, Yilang
and
Ye, Zhengyin
2017.
Active control of transonic buffet flow.
Journal of Fluid Mechanics,
Vol. 824,
Issue. ,
p.
312.
Chovet, C.
Keirsbulck, L.
Noack, B.R.
Lippert, M.
and
Foucaut, J-M.
2017.
Machine learning control for experimental shear flows targeting the reduction of a recirculation bubble.
IFAC-PapersOnLine,
Vol. 50,
Issue. 1,
p.
12307.
Chakravarthy, Satyanarayanan R.
Sampath, Ramgopal
and
Ramanan, Vikram
2017.
Dynamics and Diagnostics of Flame-Acoustic Interactions.
Combustion Science and Technology,
Vol. 189,
Issue. 3,
p.
395.
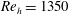 $\mathit{Re}_{h}=1350$ manipulated by a slotted jet and optically sensed by online particle image velocimetry. The feedback control law is optimized with respect to a cost functional based on the recirculation area and a penalization of the actuation. This optimization is performed employing genetic programming. After 12 generations comprised of 500 individuals, the algorithm converges to a feedback law which reduces the recirculation zone by 80 %. This machine learning control is benchmarked against the best periodic forcing which excites Kelvin–Helmholtz vortices. The machine learning control yields a new actuation mechanism resonating with the low-frequency flapping mode instability. This feedback control performs similarly to periodic forcing at the design condition but outperforms periodic forcing when the Reynolds number is varied by a factor two. The current study indicates that machine learning control can effectively explore and optimize new feedback actuation mechanisms in numerous experimental applications.
$\mathit{Re}_{h}=1350$ manipulated by a slotted jet and optically sensed by online particle image velocimetry. The feedback control law is optimized with respect to a cost functional based on the recirculation area and a penalization of the actuation. This optimization is performed employing genetic programming. After 12 generations comprised of 500 individuals, the algorithm converges to a feedback law which reduces the recirculation zone by 80 %. This machine learning control is benchmarked against the best periodic forcing which excites Kelvin–Helmholtz vortices. The machine learning control yields a new actuation mechanism resonating with the low-frequency flapping mode instability. This feedback control performs similarly to periodic forcing at the design condition but outperforms periodic forcing when the Reynolds number is varied by a factor two. The current study indicates that machine learning control can effectively explore and optimize new feedback actuation mechanisms in numerous experimental applications.


