Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T07:58:07.323Z Has data issue: false hasContentIssue false
  • English
  • Français

Clouds of bubbles in a viscoplastic fluid

Published online by Cambridge University Press:  21 September 2021

Emad Chaparian Open the ORCID record for Emad Chaparian [Opens in a new window]  and
Ian A. Frigaard Open the ORCID record for Ian A. Frigaard [Opens in a new window]
Emad Chaparian*
Affiliation:
Department of Mathematics, University of British Columbia, 1984 Mathematics Road, Vancouver, BC, V6T 1Z2, Canada
Ian A. Frigaard
Affiliation:
Department of Mathematics, University of British Columbia, 1984 Mathematics Road, Vancouver, BC, V6T 1Z2, Canada Department of Mechanical Engineering, University of British Columbia, 6250 Applied Science Lane, Vancouver, BC, V6T 1Z4, Canada
*
†Email address for correspondence: emad@math.ubc.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

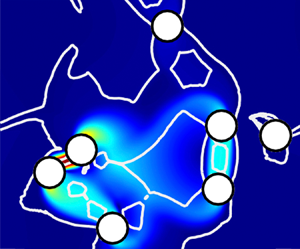
Viscoplastic fluids can hold bubbles/particles stationary by balancing the buoyancy stress with the yield stress – the key parameter here is the yield number $Y$, the ratio of the yield stress to the buoyancy stress. In the present study, we investigate a suspension of bubbles in a yield-stress fluid. More precisely, we compute how much is the gas fraction $\phi$ that could be held trapped in a yield-stress fluid without motion. Here the goal is to shed light on how the bubbles feel their neighbours through the stress field and to compute the critical yield number for a bubble cloud beyond which the flow is suppressed. We perform two-dimensional computations in a full periodic box with randomized positions of the monosized circular bubbles. A large number of configurations are investigated to obtain statistically converged results. We intuitively expect that for higher volume fractions, the critical yield number is larger. Not only here do we establish that this is the case, but also we show that short-range interactions of bubbles increase the critical yield number even more dramatically for bubble clouds. The results show that the critical yield number is a linear function of volume fraction in the dilute regime. An algebraic expression model is given to approximate the critical yield number (semi-empirically) based on the numerical experiment in the studied range of $0\le \phi \le 0.31$, together with lower and upper estimates.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Multiphase flow Non-Newtonian Flows: Plastic materials
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 927 , 25 November 2021 , R3
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahmed, R.M., Takach, N.E., Khan, U.M., Taoutaou, S., James, S., Saasen, A. & Godøy, R. 2009 Rheology of foamed cement. Cement Concrete Res. 39 (4), 353–361.CrossRefGoogle Scholar
Benge, O.G., Spangle, L.B. & Sauer, C.W. Jr. 1982 Foamed cement-solving old problems with a new technique. In SPE Annual Technical Conference and Exhibition, p. 11204. Society of Petroleum Engineers.CrossRefGoogle Scholar
Boudreau, B.P. 2012 The physics of bubbles in surficial, soft, cohesive sediments. Mar. Petrol. Geol. 38 (1), 1–18.CrossRefGoogle Scholar
Chaparian, E. & Frigaard, I.A. 2017 Yield limit analysis of particle motion in a yield-stress fluid. J. Fluid Mech. 819, 311–351.CrossRefGoogle Scholar
Chaparian, E., Izbassarov, D., De Vita, F., Brandt, L. & Tammisola, O. 2020 Yield-stress fluids in porous media: a comparison of viscoplastic and elastoviscoplastic flows. Meccanica 55 (2), 331–342.CrossRefGoogle ScholarPubMed
Chaparian, E. & Tammisola, O. 2021 Sliding flows of yield-stress fluids. J. Fluid Mech. 911, A17.CrossRefGoogle Scholar
Chaparian, E., Wachs, A. & Frigaard, I.A. 2018 Inline motion and hydrodynamic interaction of 2D particles in a viscoplastic fluid. Phys. Fluids 30 (3), 033101.CrossRefGoogle Scholar
Chateau, X., Ovarlez, G. & Trung, K.L. 2008 Homogenization approach to the behavior of suspensions of noncolloidal particles in yield stress fluids. J. Rheol. 52 (2), 489–506.CrossRefGoogle Scholar
Dagois-Bohy, S., Hormozi, S., Guazzelli, E. & Pouliquen, O. 2015 Rheology of dense suspensions of non-colloidal spheres in yield-stress fluids. J. Fluid Mech. 776, R2.CrossRefGoogle Scholar
Derakhshandeh, B. 2016 Kaolinite suspension as a model fluid for fluid dynamics studies of fluid fine tailings. Rheol. Acta 55 (9), 749–758.CrossRefGoogle Scholar
Dimakopoulos, Y., Pavlidis, M. & Tsamopoulos, J. 2013 Steady bubble rise in Herschel–Bulkley fluids and comparison of predictions via the augmented Lagrangian method with those via the Papanastasiou model. J. Non-Newtonian Fluid Mech. 200, 34–51.CrossRefGoogle Scholar
Dubash, N. & Frigaard, I.A. 2004 Conditions for static bubbles in viscoplastic fluids. Phys. Fluids 16 (12), 4319–4330.CrossRefGoogle Scholar
Feneuil, B., Roussel, N. & Pitois, O. 2020 Yield stress of aerated cement paste. Cement Concrete Res. 127, 105922.CrossRefGoogle Scholar
Frigaard, I.A. 2019 Background lectures on ideal visco-plastic fluid flows. In Lectures on Visco-Plastic Fluid Mechanics, pp. 1–40. Springer.CrossRefGoogle Scholar
Goyon, J., Bertrand, F., Pitois, O. & Ovarlez, G. 2010 Shear induced drainage in foamy yield-stress fluids. Phys. Rev. Lett. 104 (12), 128301.CrossRefGoogle ScholarPubMed
Gummalam, S. & Chhabra, R.P. 1987 Rising velocity of a swarm of spherical bubbles in a power law non-Newtonian liquid. Can. J. Chem. Engng 65 (6), 1004–1008.CrossRefGoogle Scholar
Hecht, F. 2012 New development in freefem++. J. Numer. Math. 20 (3), 251–265.CrossRefGoogle Scholar
Koblitz, A.R., Lovett, S. & Nikiforakis, N. 2018 Direct numerical simulation of particle sedimentation in a Bingham fluid. Phys. Rev. Fluids 3, 093302.CrossRefGoogle Scholar
Kogan, M., Ducloué, L., Goyon, J., Chateau, X., Pitois, O. & Ovarlez, G. 2013 Mixtures of foam and paste: suspensions of bubbles in yield stress fluids. Rheol. Acta 52 (3), 237–253.CrossRefGoogle Scholar
Ley, M.T., Folliard, K.J. & Hover, K.C. 2009 Observations of air-bubbles escaped from fresh cement paste. Cement Concrete Res. 39 (5), 409–416.CrossRefGoogle Scholar
Lopez, W.F., Naccache, M.F. & de Souza Mendes, P.R. 2018 Rising bubbles in yield stress materials. J. Rheol. 62 (1), 209–219.CrossRefGoogle Scholar
Marrucci, G. 1965 Communication. Rising velocity of swarm of spherical bubbles. Ind. Engng Chem. Fundam. 4 (2), 224–225.CrossRefGoogle Scholar
National Commission on the BP Deepwater Horizon Oil Spill and Offshore Drilling 2011 Macondo: The Gulf oil disaster. Tech. Rep. GC1221.U55 2011b.Google Scholar
Pourzahedi, A., Chaparian, E., Roustaei, A. & Frigaard, I.A. 2021 a Flow onset for a single bubble in yield-stress fluids. J. Fluid Mech. (submitted) arXiv:2107.07580.Google Scholar
Pourzahedi, A., Zare, M. & Frigaard, I.A. 2021 b Eliminating injection and memory effects in the bubble rise experiments within yield stress fluids. J. Non-Newtonian Fluid Mech. 292, 104531.CrossRefGoogle Scholar
Roquet, N. & Saramito, P. 2003 An adaptive finite element method for Bingham fluid flows around a cylinder. Comput. Meth. Appl. Mech. Engng 192 (31), 3317–3341.CrossRefGoogle Scholar
Sikorski, D., Tabuteau, H. & de Bruyn, J.R. 2009 Motion and shape of bubbles rising through a yield-stress fluid. J. Non-Newtonian Fluid Mech. 159 (1-3), 10–16.CrossRefGoogle Scholar
Small, C.C., Cho, S., Hashisho, Z. & Ulrich, A.C. 2015 Emissions from oil sands tailings ponds: review of tailings pond parameters and emission estimates. J. Petrol. Sci. Engng 127, 490–501.CrossRefGoogle Scholar
Sun, B., Pan, S., Zhang, J., Zhao, X., Zhao, Y. & Wang, Z. 2020 A dynamic model for predicting the geometry of bubble entrapped in yield stress fluid. Chem. Engng J. 391, 123569.CrossRefGoogle Scholar
Tsamopoulos, J., Dimakopoulos, Y., Chatzidai, N., Karapetsas, G. & Pavlidis, M. 2008 Steady bubble rise and deformation in Newtonian and viscoplastic fluids and conditions for bubble entrapment. J. Fluid Mech. 601, 123.CrossRefGoogle Scholar