Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wei, Wangru
Xu, Weilin
Deng, Jun
Tian, Zhong
and
Zhang, Faxing
2019.
Bubble formation and scale dependence in free-surface air entrainment.
Scientific Reports,
Vol. 9,
Issue. 1,
Kirar, Pavan Kumar
Alvarenga, Kathryn
Kolhe, Pankaj
Biswas, Gautam
and
Chandra Sahu, Kirti
2020.
Coalescence of drops on the free-surface of a liquid pool at elevated temperatures.
Physics of Fluids,
Vol. 32,
Issue. 5,
Zhu, Siqi
Kherbeche, Abderrahmane
Feng, Yumeng
and
Thoraval, Marie-Jean
2020.
Impact of an air-in-liquid compound drop onto a liquid surface.
Physics of Fluids,
Vol. 32,
Issue. 4,
Akella, V.S.
and
Gidituri, Harinadha
2020.
Universal scaling laws in droplet coalescence: A dissipative particle dynamics study.
Chemical Physics Letters,
Vol. 758,
Issue. ,
p.
137917.
Kumar, Manish
Bhardwaj, Rajneesh
and
Sahu, Kirti Chandra
2020.
Coalescence dynamics of a droplet on a sessile droplet.
Physics of Fluids,
Vol. 32,
Issue. 1,
Ren, Dong-Wei
Wu, Shuang
Yang, Juan-Cheng
and
Ni, Ming-Jiu
2020.
Investigation of liquid metal drop impingement on a liquid metal surface under the influence of a horizontal magnetic field.
Physics of Fluids,
Vol. 32,
Issue. 5,
Biswas, Gautam
and
Sahu, Kirti Chandra
2021.
Mechanical Sciences.
p.
121.
Sondermann, Carina Nogueira
Viggiano, Raphael
Rachid, Felipe Bastos de Freitas
and
Bodstein, Gustavo C.R.
2021.
A suitability analysis of transient one-dimensional two-fluid numerical models for simulating two-phase gas-liquid flows based on benchmark problems.
Computers & Fluids,
Vol. 229,
Issue. ,
p.
105070.
Wei, Yu
and
Thoraval, Marie-Jean
2021.
Maximum spreading of an impacting air-in-liquid compound drop.
Physics of Fluids,
Vol. 33,
Issue. 6,
Chaitanya, Gembali Sai
Sahu, Kirti Chandra
and
Biswas, Gautam
2021.
A study of two unequal-sized droplets undergoing oblique collision.
Physics of Fluids,
Vol. 33,
Issue. 2,
Yan, Meng
Li, Tao
Zheng, Peiru
Chen, Fan
Jiang, Yanyan
and
Li, Hui
2021.
Coalescence of Al droplet impacting on a melt surface.
Results in Physics,
Vol. 20,
Issue. ,
p.
103733.
Liu, Haihu
Lu, Yang
Li, Sheng
Yu, Yuan
and
Sahu, Kirti Chandra
2021.
Deformation and breakup of a compound droplet in three-dimensional oscillatory shear flow.
International Journal of Multiphase Flow,
Vol. 134,
Issue. ,
p.
103472.
Sarker, Anik
Boruah, Manash Protim
Randive, Pitambar R.
and
Pati, Sukumar
2021.
The role of compound droplet size on transition from jetting to bubble entrapment during its impact on liquid.
Physics of Fluids,
Vol. 33,
Issue. 10,
Behera, Manas Ranjan
Dasgupta, Anirvan
and
Chakraborty, Sudipto
2021.
Viscous diffusion induced evolution of a vortex ring.
Physics of Fluids,
Vol. 33,
Issue. 3,
Constante-Amores, C.R.
Batchvarov, A.
Kahouadji, L.
Shin, S.
Chergui, J.
Juric, D.
and
Matar, O.K.
2021.
Role of surfactant-induced Marangoni stresses in drop-interface coalescence.
Journal of Fluid Mechanics,
Vol. 925,
Issue. ,
Sattari, Amirmohammad
Tasnim, Nishat
Hanafizadeh, Pedram
and
Hoorfar, Mina
2021.
Motion and deformation of migrating compound droplets in shear-thinning fluids in a microcapillary tube.
Physics of Fluids,
Vol. 33,
Issue. 5,
Wu, Shuang
Zhang, Jie
Xiao, Qi
and
Ni, Ming-Jiu
2021.
Comparison of two interfacial flow solvers: Specific case of a single droplet impacting onto a deep pool.
Computers & Mathematics with Applications,
Vol. 81,
Issue. ,
p.
664.
Paruya, Swapan
L, Jithender Naik
and
Bhati, Jyoti
2022.
HIGH-SPEED VISUALIZATION OF TRAJECTORY AND SHAPE CHANGE OF VAPOR BUBBLE IN SUBCOOLED FLOW BOILING
.
Multiphase Science and Technology,
Vol. 34,
Issue. 4,
p.
15.
Kirar, Pavan Kumar
Kolhe, Pankaj S.
and
Sahu, Kirti Chandra
2022.
Coalescence and migration of a droplet on a liquid pool with an inclined bottom wall.
Physical Review Fluids,
Vol. 7,
Issue. 9,
Du, Jun
Zhang, Yongheng
Wei, Zhengying
Jiang, Minbo
and
Wang, Daqing
2022.
Offset impacting of a liquid aluminum droplet train on a molten pool on a horizontally moving substrate during TIG-assisted droplet deposition manufacturing.
Additive Manufacturing,
Vol. 58,
Issue. ,
p.
103039.
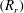 $(R_{r})$ of the compound drop while maintaining a constant liquid volume in the outer shell of the compound droplet. It is observed that for small values of the radius ratio, the coalescence dynamics is similar to that of a ‘simple’ drop, but the partial coalescence is suppressed for large values of
$(R_{r})$ of the compound drop while maintaining a constant liquid volume in the outer shell of the compound droplet. It is observed that for small values of the radius ratio, the coalescence dynamics is similar to that of a ‘simple’ drop, but the partial coalescence is suppressed for large values of 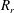 $R_{r}$. Increasing the value of
$R_{r}$. Increasing the value of 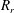 $R_{r}$ decreases the distance migrated by the inner bubble in the downward direction inside the pool. The location of the bubble after coalescence is found to play an important role in the pinch-off process of the satellite drop. The influence of the governing dimensionless parameters on the coalescence dynamics has also been investigated.
$R_{r}$ decreases the distance migrated by the inner bubble in the downward direction inside the pool. The location of the bubble after coalescence is found to play an important role in the pinch-off process of the satellite drop. The influence of the governing dimensionless parameters on the coalescence dynamics has also been investigated.