Hostname: page-component-6dbcb7884d-4kfsg Total loading time: 0 Render date: 2025-02-13T20:03:38.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherent heat transport in two-dimensional penetrative Rayleigh–Bénard convection

Published online by Cambridge University Press:  15 June 2021

Zijing Ding Open the ORCID record for Zijing Ding [Opens in a new window]  and
Jian Wu Open the ORCID record for Jian Wu [Opens in a new window]
Zijing Ding*
Affiliation:
School of Energy Science and Engineering, Harbin Institute of Technology, Harbin150001, PR China
Jian Wu
Affiliation:
School of Energy Science and Engineering, Harbin Institute of Technology, Harbin150001, PR China
*
†Email address for correspondence: z.ding@hit.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

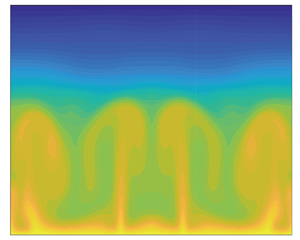
This paper investigates the steady coherent solutions, bifurcated from the linear stability of a stationary flow, in two-dimensional (2-D) penetrative convection. The results show that the thickness of the upper stably stratified layer, which is measured by $\theta _M$ (the dimensionless temperature at which the density is maximal, with $0\le \theta _M\le 1$), plays an important role in the linear and nonlinear dynamics. First, we investigate steady solutions of fixed aspect ratio $L=2{\rm \pi} /\alpha _c$ (where $\alpha _c$ is the critical wavenumber). The results show that the instability is supercritical when $\theta _M<0.4$ and is subcritical when $\theta _M>0.4$. When $\theta _M>0.4$, the results show that the type of solution depends on the Prandtl number ($Pr$). For instance, when $Pr\lesssim 2.4$ at $\theta _M=0.5$, the solution in one type of pair of convection cells does not exist, as the Rayleigh number $Ra$ exceeds a critical value due to a saddle-node bifurcation. When $Pr>2.4$, steady solutions can be found up to $Ra=10^{8}$ for all $\theta _M$, which exhibit the scaling of heat transfer (characterized by the Nusselt number $Nu$): $Nu\sim Ra^{1/4}$. Then, the optimal 2-D steady solutions are tracked up to $Ra=10^{9}$ by varying the aspect ratio $L$, which shows that heat transfer roughly follows the $Nu\sim Ra^{\gamma }$ ($\gamma \approx 1/3$) scaling in the regime of $10^{7}< Ra<10^{9}$. It is interesting that the optimal temperature field has an arm-like horizontal structure when $Pr<10$, while it has no significant horizontal structures when $Pr>10$. Thus, the mean temperature in the mixing region is higher at large $Pr$. The steady solutions show that $Nu\sim Pr^{-1/12}$ for $\theta _M=0$ in a certain range of $Pr$ by fixing the Rayleigh numbers, e.g. $1< Pr<10$ for 2-D optimal steady solutions at $Ra=10^{8}$ and $2< Pr<30$ for 2-D steady solutions of fixed aspect ratio at $Ra=10^{7}$. But when the Prandtl number is large or the upper stably stratified layer is thick, both the steady solutions of fixed aspect ratio and the 2-D optimal steady solutions are very weakly dependent on $Pr$.

JFM classification

Convection: Buoyancy-driven instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 920 , 10 August 2021 , A48
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Brummell, N., Clune, T. & Toomre, J. 2002 Penetration and overshooting in turbulent compressible convection. Astrophys. J. 570, 825–854.CrossRefGoogle Scholar
Busse, F. 1969 On Howard's upper bound for heat transport by turbulent convection. J. Fluid Mech. 37, 457–477.CrossRefGoogle Scholar
Deardorff, J., Willis, G. & Lilly, D. 1969 Laboratory investigation of non-steady penetrative convection. J. Fluid Mech. 35, 7–31.CrossRefGoogle Scholar
Chini, G.P. & Cox, S.M. 2009 Large Rayleigh number thermal convection: heat flux predictions and strongly nonlinear solutions. Phys. Fluids 21, 083603.CrossRefGoogle Scholar
Ding, Z. & Kerswell, R.R. 2020 Exhausting the background approach for bounding heat flux in Rayleigh–Bénard convection. J. Fluid Mech. 889, A33.CrossRefGoogle Scholar
Dintrans, B., Brandenburg, A., Nordlund, Å. & Stein, R. 2005 Spectrum and amplitudes of internal gravity waves excited by penetrative convection in solar-type stars. Astron. Astrophys. 438, 365–376.CrossRefGoogle Scholar
Doering, C. & Constantin, P. 1992 Energy dissipation in shear driven turbulence. Phys. Rev. Lett. 69, 1648.CrossRefGoogle ScholarPubMed
Doering, C. & Constantin, P. 1994 Variational bounds on energy dissipation in incompressible flows: shear flow. Phys. Rev. E 49, 4087.CrossRefGoogle ScholarPubMed
Doering, C. & Constantin, P. 1996 Variational bounds on energy dissipation in incompressible flows. III. Convection. Phys. Rev. E 53, 5957.CrossRefGoogle ScholarPubMed
Gebhart, B. & Mollendorf, J. 1977 A new density relation for pure and saline water. Deep-Sea Res. 24, 831–848.CrossRefGoogle Scholar
Goluskin, D. & Spiegel, E. 2012 Convection driven by internal heating. Phys. Lett. A 377, 83–92.CrossRefGoogle Scholar
Goluskin, D. & van der Poel, E. 2016 Penetrative internally heated convection in two and three dimensions. J. Fluid Mech. 791, R6.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Howard, L. 1963 Heat transport by turbulent convection. J. Fluid Mech. 17, 405–432.CrossRefGoogle Scholar
Joseph, D.D. 1976 Stability of Fluid Motions II. Springer.CrossRefGoogle Scholar
Kerswell, R.R. 1997 Variational bounds on shear-driven turbulence and turbulent Boussinesq convection. Physica D 100, 355–376.CrossRefGoogle Scholar
Kerswell, R.R. 1998 Unification of variational principles for turbulent shear flows: the background method of Doering–Constantin and Howard–Busse's mean-fluctuation formulation. Physica D 121, 175–192.CrossRefGoogle Scholar
Kraichnan, R.H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5, 1374–1389.CrossRefGoogle Scholar
Landau, L. & Lifshitz, E. 2004 Fluid Mechanics, 2nd edn. Elservier.Google Scholar
Lecoanet, D., Le Bars, M., Burns, K., Vasil, G., Brown, B., Quataert, E. & Oishi, J. 2015 Numerical simulations of internal wave generation by convection in water. Phys. Rev. E 91, 063016.CrossRefGoogle ScholarPubMed
Malkus, M. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Moore, D. & Weiss, N. 1973 Nonlinear penetrative convection. J. Fluid Mech. 61, 553–581.CrossRefGoogle Scholar
Motoki, S., Kawahara, G. & Shimizu, M. 2020 Multi-scale steady solution for Rayleigh–Bénard convection. arXiv:2004.06868v1.CrossRefGoogle Scholar
Musman, S. 1968 Penetrative convection. J. Fluid Mech. 31, 343–360.CrossRefGoogle Scholar
Payne, L.E. & Straughan, B. 1987 Unconditional nonlinear stability in penetrative convetion. Geophys. Astrophys. Fluid Dyn. 39, 57–63.CrossRefGoogle Scholar
Plasting, S.C. & Kerswell, R.R. 2003 Improved upper bound on the energy dissipation rate in plane Couette flow: the full solution to Busse's problem and the Constantin-Doering-Hopf problem with one-dimensional background field. J. Fluid Mech. 16, 363–379.Google Scholar
van der Poel, E., Stevens, R. & Lohse, D. 2011 Connecting flow structures and heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. E 84, 045303.CrossRefGoogle ScholarPubMed
Seis, C. 2015 Scaling bounds on dissipation in turbulent flows. J. Fluid Mech. 777, 591–603.CrossRefGoogle Scholar
Sondak, D., Smith, L. & Waleffe, F. 2015 Optimal heat transport solutions for Rayleigh–Bénard convection. J. Fluid Mech. 784, 565–595.CrossRefGoogle Scholar
Tennekes, H. 1973 A model for the dynamics of the inversion above a convective boundary layer. J. Atmos. Sci. 30, 558–567.2.0.CO;2>CrossRefGoogle Scholar
Toppaladoddi, S. & Wettlaufer, J. 2018 Penetrative convection at high Rayleigh numbers. Phys. Rev. Fluids 3, 043501.CrossRefGoogle Scholar
Townsend, A. 1964 Natural convection in water over an ice surface. Q.J.R. Meteorol. Soc. 101, 248–259.CrossRefGoogle Scholar
Tuckerman, L.S., Langham, J. & Willis, A.P. 2018 Order-of-magnitude speedup for steady states and traveling waves via Stokes preconditioning in Channeflow and Openpipeflow. In Computational Modelling of Bifurcations and Instabilities in Fluid Dynamics (ed. Alexander Gelfgat). Computational Methods in Applied Sciences, Springer.CrossRefGoogle Scholar
Veronis, G. 1963 Penetrative convection. Astrophys. J. 137, 641–663.CrossRefGoogle Scholar
Waleffe, F., Boonkasame, A. & Smith, L. 2015 Heat transport by coherent Rayleigh–Bénard convectioin. Phys. Fluids 27, 051702.CrossRefGoogle Scholar
Wang, Q., Zhou, Q., Wan, Z. & Sun, D. 2019 Penetrative turbulent Rayleigh–Bénard convection in two and three dimensions. J. Fluid Mech. 870, 718–734.CrossRefGoogle Scholar
Wang, Q., Verzicco, R., Lohse, D. & Shishkina, O. 2020 Multiple states in turbulent large-aspect ratio thermal convection: what determines the number of convection rolls? Phys. Rev. Lett. 125, 074501.CrossRefGoogle ScholarPubMed
Wen, B., Goluskin, D., LeDuc, M., Chini, G. & Doering, C. 2020 Steady Rayleigh–Bénard convection between stress-free boundaries. J. Fluid Mech. 905, R4.CrossRefGoogle Scholar
Wen, B., Goluskin, D. & Doering, C. 2020 Steady Rayleigh–Bénard convection between no-slip boundaries. arXiv:2008.08752v1.CrossRefGoogle Scholar
Willis, A.P. 2017 The Openpipeflow Navier–Stokes solver. SoftwareX 6, 124–127.CrossRefGoogle Scholar
Zhu, X., Mathai, V., Stevens, R.J.A.M., Verzicco, R. & Lohse, D. 2018 Transition to the ultimate regime in two-dimensional Rayleigh–Bénardnard convection. Phys. Rev. Lett. 120, 144502.CrossRefGoogle ScholarPubMed