Article contents
Coherent structure detection and the inverse cascade mechanism in two-dimensional Navier–Stokes turbulence
Published online by Cambridge University Press: 19 May 2023
Abstract
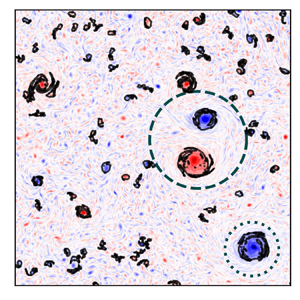
Coherent structures in two-dimensional Navier–Stokes turbulence are ubiquitously observed in nature, experiments and numerical simulations. The present study conducts a comparison between several structure detection schemes based on the Okubo–Weiss criterion, the vorticity magnitude and Lagrangian coherent structures (LCSs), focusing on the inverse cascade in two-dimensional hydrodynamic turbulence. A recently introduced vortex scaling phenomenology (Burgess & Scott, J. Fluid Mech., vol. 811, 2017, pp. 742–756) allows the quantification of the respective thresholds required by these methods based on physical properties of the flow. The resulting improved comparability allows us to identify characteristic relative differences in the detection sensitivity between the employed structure detection techniques. With respect to the inverse cascade of energy, coherent structures contribute, as expected, substantially less to the cross-scale flux than the residual incoherent parts of the flow although the energetically dominant coherent structures lead to an important large-scale deformation of the energy spectrum. This cascade inactivity can be understood by an increased misalignment of strain-rate and subgrid stress tensors within coherent structures. At the same time, the structures exhibit strong and localised nonlinear cross-scale interactions that appear to stabilise them. We quantify and interpret the resulting shape preservation of coherent structures in terms of a multi-scale gradient approach (Eyink, J. Fluid Mech., vol. 549, 2006, pp. 191–214) as the depletion of strain rotation and vorticity gradient stretching whereas the dynamics of the residual fluctuations are consistent with the vortex thinning picture.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 2
- Cited by


