Article contents
Competition between the centrifugal and strato-rotational instabilities in the stratified Taylor–Couette flow
Published online by Cambridge University Press: 06 February 2018
Abstract
The stably stratified Taylor–Couette flow is investigated experimentally and numerically through linear stability analysis. In the experiments, the stability threshold and flow regimes have been mapped over the ranges of outer and inner Reynolds numbers: 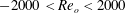 $-2000<Re_{o}<2000$ and
$-2000<Re_{o}<2000$ and 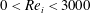 $0<Re_{i}<3000$ , for the radius ratio
$0<Re_{i}<3000$ , for the radius ratio 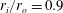 $r_{i}/r_{o}=0.9$ and the Brunt–Väisälä frequency
$r_{i}/r_{o}=0.9$ and the Brunt–Väisälä frequency 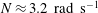 $N\approx 3.2~\text{rad}~\text{s}^{-1}$ . The corresponding Froude numbers
$N\approx 3.2~\text{rad}~\text{s}^{-1}$ . The corresponding Froude numbers 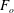 $F_{o}$ and
$F_{o}$ and 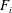 $F_{i}$ are always much smaller than unity. Depending on
$F_{i}$ are always much smaller than unity. Depending on 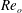 $Re_{o}$ (or equivalently on the angular velocity ratio
$Re_{o}$ (or equivalently on the angular velocity ratio 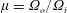 $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6FA}_{o}/\unicode[STIX]{x1D6FA}_{i}$ ), three different regimes have been identified above instability onset: a weakly non-axisymmetric mode with low azimuthal wavenumber
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6FA}_{o}/\unicode[STIX]{x1D6FA}_{i}$ ), three different regimes have been identified above instability onset: a weakly non-axisymmetric mode with low azimuthal wavenumber 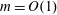 $m=O(1)$ is observed for
$m=O(1)$ is observed for 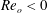 $Re_{o}<0$ (
$Re_{o}<0$ ( 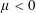 $\unicode[STIX]{x1D707}<0$ ), a highly non-axisymmetric mode with
$\unicode[STIX]{x1D707}<0$ ), a highly non-axisymmetric mode with 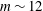 $m\sim 12$ occurs for
$m\sim 12$ occurs for 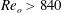 $Re_{o}>840$ (
$Re_{o}>840$ ( 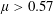 $\unicode[STIX]{x1D707}>0.57$ ) while both modes are present simultaneously in the lower and upper parts of the flow for
$\unicode[STIX]{x1D707}>0.57$ ) while both modes are present simultaneously in the lower and upper parts of the flow for 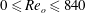 $0\leqslant Re_{o}\leqslant 840$ (
$0\leqslant Re_{o}\leqslant 840$ ( 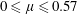 $0\leqslant \unicode[STIX]{x1D707}\leqslant 0.57$ ). The destabilization of these primary modes and the transition to turbulence as
$0\leqslant \unicode[STIX]{x1D707}\leqslant 0.57$ ). The destabilization of these primary modes and the transition to turbulence as 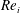 $Re_{i}$ increases have been also studied. The linear stability analysis proves that the weakly non-axisymmetric mode is due to the centrifugal instability while the highly non-axisymmetric mode comes from the strato-rotational instability. These two instabilities can be clearly distinguished because of their distinct dominant azimuthal wavenumber and frequency, in agreement with the recent results of Park et al. (J. Fluid Mech., vol. 822, 2017, pp. 80–108). The stability threshold and the characteristics of the primary modes observed in the experiments are in very good agreement with the numerical predictions. Moreover, we show that the centrifugal and strato-rotational instabilities are observed simultaneously for
$Re_{i}$ increases have been also studied. The linear stability analysis proves that the weakly non-axisymmetric mode is due to the centrifugal instability while the highly non-axisymmetric mode comes from the strato-rotational instability. These two instabilities can be clearly distinguished because of their distinct dominant azimuthal wavenumber and frequency, in agreement with the recent results of Park et al. (J. Fluid Mech., vol. 822, 2017, pp. 80–108). The stability threshold and the characteristics of the primary modes observed in the experiments are in very good agreement with the numerical predictions. Moreover, we show that the centrifugal and strato-rotational instabilities are observed simultaneously for 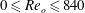 $0\leqslant Re_{o}\leqslant 840$ in the lower and upper parts of the flow, respectively, because of the variations of the local Reynolds numbers along the vertical due to the salinity gradient.
$0\leqslant Re_{o}\leqslant 840$ in the lower and upper parts of the flow, respectively, because of the variations of the local Reynolds numbers along the vertical due to the salinity gradient.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 11
- Cited by


