Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T07:25:54.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Compressible flow at high pressure with linear equation of state

Published online by Cambridge University Press:  21 March 2018

William A. Sirignano Open the ORCID record for William A. Sirignano [Opens in a new window]
Get access Rights & Permissions [Opens in a new window]

Abstract

Compressible flow varies from ideal-gas behaviour at high pressures where molecular interactions become important. It is widely accepted that density is well described through a cubic equation of state while enthalpy and sound speed are functions of both temperature and pressure, based on two parameters, 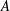$A$ and 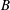$B$, related to intermolecular attraction and repulsion, respectively. Assuming small variations from ideal-gas behaviour, a closed-form approximate solution is obtained that is valid over a wide range of conditions. An expansion in these molecular interaction parameters simplifies relations for flow variables, elucidating the role of molecular repulsion and attraction in variations from ideal-gas behaviour. Real-gas modifications in density, enthalpy and sound speed for a given pressure and temperature lead to variations in many basic compressible-flow configurations. Sometimes, the variations can be substantial in quantitative or qualitative terms. The new approach is applied to choked-nozzle flow, isentropic flow, nonlinear wave propagation and flow across a shock wave, all for a real gas. Modifications are obtained for allowable mass flow through a choked nozzle, nozzle thrust, sonic wave speed, Riemann invariants, Prandtl’s shock relation and the Rankine–Hugoniot relations. Forced acoustic oscillations can show substantial augmentation of pressure amplitudes when real-gas effects are taken into account. Shocks at higher temperatures and pressures can have larger pressure jumps with real-gas effects. Weak shocks decay to zero strength at sonic speed. The proposed framework can rely on any cubic equation of state and can be applied to multicomponent flows or to more complex flow configurations.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Gas dynamics Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 244 - 292
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anand, R. K. 2012 Jump relations across a shock in non-ideal gas flow. Astrophys. Space Sci. 342, 377–388.10.1007/s10509-012-1175-6Google Scholar
Arina, R. 2004 Numerical simulation of near-critical fluids. Appl. Numer. Maths 51, 409–426.10.1016/j.apnum.2004.06.002Google Scholar
Ascough, J. C.1968 Real-air effects in propelling nozzles. Ministry of Technology, Aeronautical Research Council Reports and Memoranda 3522.Google Scholar
Chueh, P. L. & Prausnitz, J. M. 1967a Vapor–liquid equilibria at high pressures. Vapor-phase fugacity coefficients in nonpolar and quantum-gas mixtures. Ind. Engng Chem. Fundam. 6, 492–498.10.1021/i160024a003Google Scholar
Chueh, P. L. & Prausnitz, J. M. 1967b Vapor–liquid equilibria at high pressures. Calculation of partial molar volumes in nonpolar liquid mixtures. AIChE J. 13, 1099.10.1002/aic.690130612Google Scholar
Colella, P. & Glaz, H. M. 1985 Efficient algorithms for the Riemann problem for real gases. J. Comput. Phys. 59, 264–289.Google Scholar
Crocco, L. 1958 One-dimensional treatment of steady gas dynamics. In Fundamentals of Gas Dynamics, High Speed Aerodynamics and Jet Propulsion (ed. Emmons, H. W.), vol. III, pp. 64–349. Princeton University Press.10.1515/9781400877539-004Google Scholar
Donaldson, C. D. & Jones, J. J.1951 Some measurements of the effect of gaseous imperfections on the critical pressure ratio in air and the speed of sound in nitrogen. NACA Technical Note 2437.Google Scholar
Drikakis, D. & Tsangaris, S. 1993 Real gas effects for compressible nozzle flows. Trans. ASME J. Fluids Engng 115, 115–120.10.1115/1.2910092Google Scholar
Glaister, P. 1988 An approximate linearized Riemann solver for the Euler equations for real gases. J. Comput. Phys. 74, 382–408.10.1016/0021-9991(88)90084-8Google Scholar
Graboski, M. S. & Daubert, T. E. 1978 A modified Soave equation of state for phase equilibrium calculations. 1. Hydrocarbon systems. Ind. Engng Chem. Process Des. Dev. 17, 443–448.10.1021/i260068a009Google Scholar
Guardone, A. & Vigevano, L. 2002 Roe linearization for the van der Waals gas. J. Comput. Phys. 175, 50–78.10.1006/jcph.2001.6915Google Scholar
Jassim, E., Abedinzadegan Abdi, M. & Muzychka, Y. 2008 Computational fluid dynamics study for flow of natural gas through high-pressure supersonic nozzles: Part 1. Real gas effects and shockwave. Petrol. Sci. Tech. 26, 1757–1772.10.1080/10916460701287847Google Scholar
Johnson, R. C. 1964 Calculations of real-gas effects in flow through critical-flow nozzles. ASME J. Basic Engng 86 (3), 519–525.10.1115/1.3653160Google Scholar
Jorda-Juanos, A. & Sirignano, W. A. 2016 Pressure effects on real-gas laminar counterflow. Combust. Flame 181, 54–70.10.1016/j.combustflame.2017.01.030Google Scholar
Kim, J.-H., Kim, H.-D., Setoguchi, T. & Matsuo, S. 2008 Computational study on the critical nozzle flow of high-pressure hydrogen gas. J. Propul. Power 24, 715–721.10.2514/1.30976Google Scholar
Kluwick, A. 1993 Transonic nozzle flow of dense gases. J. Fluid Mech. 247, 661–688.10.1017/S0022112093000618Google Scholar
Kouremenos, D. A. 1986 The normal shock waves of real gases and the generalized isentropic exponents. Forsch. Ing. 52.Google Scholar
Kouremenos, D. A. & Antonopoulos, K. A. 1989 Real gas normal shock waves with the Redlich–Kwong equation of state. Acta Mechanica 76, 223–233.10.1007/BF01253581Google Scholar
Lapuerta, M., Ballesteros, R. & Agudelo, J. R. 2006 Effect of the gas state equation on the thermodynamic diagnostic of diesel combustion. Appl. Therm. Engng 26, 1492–1499.10.1016/j.applthermaleng.2006.01.001Google Scholar
Liepmann, H. W. & Roshko, A. 1957 Elements of Gasdynamics. Wiley.10.1063/1.3060140Google Scholar
Meng, H. & Yang, V. 2003 A unified treatment of general fluid thermodynamics and its application to a preconditioning scheme. J. Comput. Phys. 189, 277–304.10.1016/S0021-9991(03)00211-0Google Scholar
Poling, B. E., Prausnitz, J. M. & O’Connell, J. P. 2001 The Properties of Gases and Liquids, 5th edn. McGraw-Hill.Google Scholar
Saad, M. A. 1993 Compressible Fluid Flow, 2nd edn. Prentice-Hall.Google Scholar
Soave, G. 1972 Equilibrium constants from a modified Redlich–Kwong equation of state. Chem. Engng Sci. 27, 1197–1203.10.1016/0009-2509(72)80096-4Google Scholar
Tao, L. N. 1955 Gas dynamic behavior of real gases. J. Aero. Sci. 22 (11), 763–774.10.2514/8.3456Google Scholar
Tsien, H. S. 1946 One-dimensional flow of a gas characterized by van der Waals equation of state. Stud. Appl. Maths 25, 301–324.Google Scholar
Wilson, J. L. & Regan, J. D1965 A simple method for real gas flow calculations. Ministry of Aviation, London, Current Paper 772.Google Scholar