Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T06:47:51.793Z Has data issue: false hasContentIssue false
  • English
  • Français

Computational modelling and analysis of haemodynamics in a simple model of aortic stenosis

Published online by Cambridge University Press:  19 July 2018

Chi Zhu Open the ORCID record for Chi Zhu [Opens in a new window] ,
Jung-Hee Seo  and
Rajat Mittal
Chi Zhu
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Jung-Hee Seo
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Rajat Mittal*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: mittal@jhu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

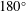In a study motivated by considerations associated with heart murmurs and cardiac auscultation, numerical simulations are used to analyse the haemodynamics in a simple model of an aorta with an aortic stenosis. The aorta is modelled as a curved pipe with a $180^{\circ }$ turn, and three different stenoses with area reductions of 50 %, 62.5 % and 75 % are examined. A uniform steady inlet velocity with a Reynolds number of 2000 is used for all of the cases and direct numerical simulation is employed to resolve the dynamics of the flow. The poststenotic flow is dominated by the jet that originates from the stenosis as well as the secondary flow induced by the curvature, and both contribute significantly to the flow turbulence. On the anterior surface of the modelled aorta, the location with maximum pressure fluctuation, which may be considered as the source location for the murmurs, is found to be located around 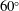$60^{\circ }$ along the aortic arch, and this location is relatively insensitive to the severity of the stenosis. For all three cases, this high-intensity wall pressure fluctuation includes contributions from both the jet and the secondary flow. Spectral analysis shows that for all three stenoses, the Strouhal number of the vortex shedding of the jet shear layer is close to 0.93, which is higher than the shedding frequency of a corresponding free jet or a jet confined in a straight pipe. This frequency also appears in the pressure spectra at the location postulated as the source of the murmurs, in the form of a ‘break frequency.’ The implications of these findings for cardiac auscultation-based diagnosis of aortic stenosis are also discussed.

JFM classification

Biological Fluid Dynamics: Biomedical flows Biological Fluid Dynamics: Blood flow Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 23 - 49
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmed, S. A. 1998 An experimental investigation of pulsatile flow through a smooth constriction. Exp. Therm. Fluid Sci. 17 (4), 309–318.Google Scholar
Ahmed, S. A. & Giddens, D. P. 1983a Velocity measurements in steady flow through axisymmetric stenoses at moderate Reynolds numbers. J. Biomech. 16 (7), 505–516.Google Scholar
Ahmed, S. A. & Giddens, D. P. 1983b Flow disturbance measurements through a constricted tube at moderate Reynolds numbers. J. Biomech. 16 (12), 955–963.Google Scholar
Ahmed, S. A. & Giddens, D. P. 1984 Pulsatile poststenotic flow studies with laser Doppler anemometry. J. Biomech. 17 (9), 695–705.Google Scholar
Alam, U., Asghar, O., Khan, S. Q., Hayat, S. & Malik, R. A. 2010 Cardiac auscultation: an essential clinical skill in decline. British J. Cardiol. 17 (1), 8–10.Google Scholar
Andreou, A. G., Abraham, T., Thompson, W. R., Seo, J. H. & Mittal, R. 2015 Mapping the cardiac acousteome: an overview of technologies, tools and methods. In 2015 49th Annual Conference on Information Sciences and Systems (CISS), pp. 1–6. IEEE.Google Scholar
Back, L. H. & Roschke, E. J. 1972 Shear-layer flow regimes and wave instabilities and reattachment lengths downstream of an abrupt circular channel expansion. Trans. ASME J. Appl. Mech. 39 (3), 677–681.Google Scholar
Beavers, G. S. & Wilson, T. A. 1970 Vortex growth in jets. J. Fluid Mech. 44 (1), 97–112.Google Scholar
Berger, S. A. & Jou, L.-D. 2000 Flows in stenotic vessels. Annu. Rev. Fluid Mech. 32, 347–382.Google Scholar
Bickley, L. & Szilagyi, P. G. 2012 Bates’ Guide to Physical Examination and History-taking. Lippincott Williams & Wilkins.Google Scholar
Blackburn, H. M. & Sherwin, S. J. 2007 Instability modes and transition of pulsatile stenotic flow: pulse-period dependence. J. Fluid Mech. 573, 57–88.Google Scholar
Bulusu, K. V., Hussain, S. & Plesniak, M. W. 2014 Determination of secondary flow morphologies by wavelet analysis in a curved artery model with physiological inflow. Exp. Fluids 55 (11), 1832–1852.Google Scholar
Cassanova, R. A. & Giddens, D. P. 1978 Disorder distal to modeled stenoses in steady and pulsatile flow. J. Biomech. 11 (10–12), 441–453.Google Scholar
Clark, C. 1976a The fluid mechanics of aortic stenosis. Part I. Theory and steady flow experiments. J. Biomech. 9 (8), 521–528.Google Scholar
Clark, C. 1976b The fluid mechanics of aortic stenosis. Part II. Unsteady flow experiments. J. Biomech. 9 (9), 567–573.Google Scholar
Clark, C. 1976c Turbulent velocity measurements in a model of aortic stenosis. J. Biomech. 9 (11), 677–687.Google Scholar
Clark, C. 1977 Turbulent wall pressure measurements in a model of aortic stenosis. J. Biomech. 10 (8), 461–472.Google Scholar
Clark, C. 1980 The propagation of turbulence produced by a stenosis. J. Biomech. 13 (7), 591–604.Google Scholar
Dean, W. R. 1927 Note on the motion of fluid in a curved pipe. Lond. Edin. Dublin Philos. Mag. J. Sci. 4 (20), 208–223.Google Scholar
Duncan, G. W., Gruber, J. O., Dewey, C. F. Jr, Myers, G. S. & Lees, R. S. 1975 Evaluation of carotid stenosis by phonoangiography. New England J. Med. 293 (22), 1124–1128.Google Scholar
Dvinsky, A. S. & Ojha, M. 1994 Simulation of three-dimensional pulsatile flow through an asymmetric stenosis. Med. Biol. Engng Comput. 32 (2), 138–142.Google Scholar
Erne, P. 2008 Beyond auscultation: acoustic cardiography in the diagnosis and assessment of cardiac disease. Swiss Med. Weekly 138 (31–32), 439–452.Google Scholar
Etchells, E., Bell, C. & Robb, K. 1997 Does this patient have an abnormal systolic murmur? Jama 277 (7), 564–571.Google Scholar
Fredberg, J. J. 1977 Origin and character of vascular murmurs: model studies. J. Acoust. Soc. Am. 61 (4), 1077–1085.Google Scholar
Govindaraju, K., Viswanathan, G. N., Badruddin, I. A., Kamangar, S., Salman Ahmed, N. J. & Al-Rashed, A. 2016 The influence of artery wall curvature on the anatomical assessment of stenosis severity derived from fractional flow reserve: a computational fluid dynamics study. Comput. Meth. Biomech. Biomed. Engng 19 (14), 1541–1549.Google Scholar
Griffith, B. E. 2010 Immersed boundary model of aortic heart valve dynamics with physiological driving and loading conditions. Intl J. Numer. Meth. Biomed. Engng 26 (1), 807–827.Google Scholar
Hanna, I. R. & Silverman, M. E. 2002 A history of cardiac auscultation and some of its contributors. Am. J. Cardiol. 90 (3), 259–267.Google Scholar
Hathcock, J. J. 2006 Flow effects on coagulation and thrombosis. Arterioscler. Thromb. Vasc. Biol. 26 (8), 1729–1737.Google Scholar
Hinze, J. 1975 Turbulence. McGraw-Hill.Google Scholar
Huang, R. F., Ho, C.-Y. & Chen, J.-K. 2011 Pulsatile flow patterns and wall shear stresses in arch of a turn-around tube with/without stenosis. J. Mech. 27 (1), 79–94.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jin, S., Oshinski, J. & Giddens, D. P. 2003 Effects of wall motion and compliance on flow patterns in the ascending aorta. Trans. ASME J. Biomech. Engng 125 (3), 347–354.Google Scholar
Johansen, F. C. 1930 Flow through pipe orifices at low Reynolds numbers. Proc. R. Soc. Lond. A 126 (801), 231–245.Google Scholar
Karmonik, C., Bismuth, J., Davies, M. G., Shah, D. J., Younes, H. K. & Lumsden, A. B. 2011 A computational fluid dynamics study pre- and post-stent graft placement in an acute type B aortic dissection. Vasc. Endovascular Surg. 45 (2), 157–164.Google Scholar
Lee, K. E., Parker, K. H., Caro, C. G. & Sherwin, S. J. 2008 The spectral/hp element modelling of steady flow in non-planar double bends. Intl J. Numer. Meth. Fluids 57 (5), 519–529.Google Scholar
Lees, R. S. & Dewey, C. F. 1970 Phonoangiography: a new noninvasive diagnostic method for studying arterial disease. Proc. Natl Acad. Sci. USA 67 (2), 935–942.Google Scholar
Lieber, B. B. & Giddens, D. P. 1990 Post-stenotic core flow behavior in pulsatile flow and its effects on wall shear stress. J. Biomech. 23 (6), 597–605.Google Scholar
Liu, B. 2007 The influences of stenosis on the downstream flow pattern in curved arteries. Med. Engng Phys. 29 (8), 868–876.Google Scholar
Long, Q., Xu, X. Y., Ramnarine, K. V. & Hoskins, P. 2001 Numerical investigation of physiologically realistic pulsatile flow through arterial stenosis. J. Biomech. 34 (10), 1229–1242.Google Scholar
Lu, P. C., Hui, C. N. & Hwang, N. H. C. 1983 A model investigation of the velocity and pressure spectra in vascular murmurs. J. Biomech. 16 (11), 923–931.Google Scholar
Mahmoudi Zarandi, M.2000 Steady and pulsatile flow in curved vessels. PhD thesis, California Institute of Technology.Google Scholar
Manning, W. J. 2013 Asymptomatic aortic stenosis in the elderly: a clinical review. Jama 310 (14), 1490–1497.Google Scholar
Mittal, R., Dong, H., Bozkurttas, M., Najjar, F. M., Vargas, A. & von Loebbecke, A. 2008 A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 227 (10), 4825–4852.Google Scholar
Mittal, R., Seo, J. H., Shoele, K. & Resar, J. 2017 A novel computational model for predicting thrombosis risk in bioprosthetic transcatheter aortic valves. In Heart Valve Society 4th Annual Meeting.Google Scholar
Mittal, R., Simmons, S. P. & Najjar, F. 2003 Numerical study of pulsatile flow in a constricted channel. J. Fluid Mech. 485, 337–378.Google Scholar
Mittal, R., Simmons, S. P. & Udaykumar, H. S. 2001 Application of large-eddy simulation to the study of pulsatile flow in a modeled arterial stenosis. Trans. ASME J. Biomech. Engng 123 (4), 325–332.Google Scholar
Mohamied, Y., Rowland, E. M., Bailey, E. L., Sherwin, S. J., Schwartz, M. A. & Weinberg, P. D. 2014 Change of direction in the biomechanics of atherosclerosis. Ann. Biomed. Engng 43 (1), 16–25.Google Scholar
Morbiducci, U., Ponzini, R., Rizzo, G., Cadioli, M., Esposito, A., Montevecchi, F. M. & Redaelli, A. 2011 Mechanistic insight into the physiological relevance of helical blood flow in the human aorta: an in vivo study. Biomech. Model. Mechanobiol. 10 (3), 339–355.Google Scholar
Niu, Y.-Y., Chu, W.-K., Lee, L.-C. & Yu, H.-Y. 2002 Numerical evaluation of curvature effects on shear stresses across arterial stenoses. Biomed. Engng: Appl., Basis Commun. 14 (4), 164–170.Google Scholar
Ojha, M., Cobbold, R. S. C., Johnston, K. W. & Hummel, R. L. 1989 Pulsatile flow through constricted tubes: an experimental investigation using photochromic tracer methods. J. Fluid Mech. 203, 173–197.Google Scholar
Okpara, E. & Agarwal, R. 2007 Numerical simulation of steady and pulsatile flow through models of vascular and aortic valve stenoses. In 37th AIAA Fluid Dynamics Conference and Exhibit, American Institute of Aeronautics and Astronautics.Google Scholar
Pedley, T. J. 1980 The Fluid Mechanics of Large Blood Vessels, Cambridge Monographs on Mechanics, vol. 1. Cambridge University Press.Google Scholar
Peiffer, V., Rowland, E. M., Cremers, S. G., Weinberg, P. D. & Sherwin, S. J. 2012 Effect of aortic taper on patterns of blood flow and wall shear stress in rabbits: association with age. Atherosclerosis 223 (1), 114–121.Google Scholar
Peiffer, V., Sherwin, S. J. & Weinberg, P. D. 2013 Does low and oscillatory wall shear stress correlate spatially with early atherosclerosis? A systematic review. Cardiovascular Res. 99 (2), 242–250.Google Scholar
Semmlow, J. & Rahalkar, K. 2007 Acoustic detection of coronary artery disease. Annu. Rev. Biomed. Engng 9, 449–469.Google Scholar
Seo, J. H., Bakhshaee, H., Garreau, G., Zhu, C., Andreou, A., Thompson, W. R. & Mittal, R. 2017 A method for the computational modeling of the physics of heart murmurs. J. Comput. Phys. 336, 546–568.Google Scholar
Seo, J. H. & Mittal, R. 2011 A sharp-interface immersed boundary method with improved mass conservation and reduced spurious pressure oscillations. J. Comput. Phys. 230 (19), 7347–7363.Google Scholar
Seo, J. H. & Mittal, R. 2012 A coupled flow–acoustic computational study of bruits from a modeled stenosed artery. Med. Biol. Engng Comput. 50 (10), 1025–1035.Google Scholar
Sherwin, S. J. & Blackburn, H. M. 2005 Three-dimensional instabilities of steady and pulsatile axisymmetric stenotic flows. J. Fluid Mech. 533, 297–327.Google Scholar
Stein, P. D. & Sabbah, H. N. 1976 Turbulent blood flow in the ascending aorta of humans with normal and diseased aortic valves. Circulat. Res 39 (1), 58–65.Google Scholar
Stein, P. D., Walburn, F. J. & Sabbah, H. N. 1982 Turbulent stresses in the region of aortic and pulmonary valves. Trans. ASME J. Biomech. Engng 104 (3), 238–244.Google Scholar
Taelman, L., Bols, J., Degroote, J., Muthurangu, V., Panzer, J., Vierendeels, J. & Segers, P. 2015 Differential impact of local stiffening and narrowing on hemodynamics in repaired aortic coarctation: an FSI study. Med. Biol. Engng Comput. 54 (2), 497–510.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.Google Scholar
Tobin, R. J. & Chang, I.-dee 1976 Wall pressure spectra scaling downstream of stenoses in steady tube flow. J. Biomech. 9 (10), 633–640.Google Scholar
de Tullio, M. D. & Pascazio, G. 2016 A moving-least-squares immersed boundary method for simulating the fluid–structure interaction of elastic bodies with arbitrary thickness. J. Comput. Phys. 325, 201–225.Google Scholar
Varghese, S. S. 2003 Numerical modeling of pulsatile turbulent flow in stenotic vessels. Trans. ASME J. Biomech. Engng 125 (4), 445–460.Google Scholar
Varghese, S. S., Frankel, S. H. & Fischer, P. F. 2007a Direct numerical simulation of stenotic flows. Part 1. Steady flow. J. Fluid Mech. 582, 253–280.Google Scholar
Varghese, S. S., Frankel, S. H. & Fischer, P. F. 2007b Direct numerical simulation of stenotic flows. Part 2. Pulsatile flow. J. Fluid Mech. 582, 281–318.Google Scholar
Watrous, R. L., Reid Thompson, W. & Ackerman, S. J. 2008 The impact of computer-assisted auscultation on physician referrals of asymptomatic patients with heart murmurs. Clin. Cardiol. 31 (2), 79–83.Google Scholar
Yellin, E. L. 1966 Hydraulic noise in submerged and bounded liquid jets. In Biomed. Fluid Mechan. Symposium, pp. 209–221. American Society of Mechanical Engineers.Google Scholar
Zhu, C., Seo, J.-H., Bakhshaee, H. & Mittal, R. 2017 A computational method for analyzing the biomechanics of arterial bruits. Trans. ASME J. Biomech. Engng 139 (5), 051008.Google Scholar