Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-14T23:00:53.637Z Has data issue: false hasContentIssue false
  • English
  • Français

A conjecture on the least stable mode for the energy stability of plane parallel flows

Published online by Cambridge University Press:  29 October 2019

Xiangming Xiong Open the ORCID record for Xiangming Xiong [Opens in a new window]  and
Zhi-Min Chen Open the ORCID record for Zhi-Min Chen [Opens in a new window]
Xiangming Xiong
Affiliation:
School of Mathematics and Statistics, Shenzhen University, Shenzhen, 518060, China The Program in Applied and Computational Mathematics, Princeton University, Princeton, NJ 08544, USA
Zhi-Min Chen*
Affiliation:
School of Mathematics and Statistics, Shenzhen University, Shenzhen, 518060, China
*
†Email address for correspondence: zmchen@szu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In the energy stability theory, the critical Reynolds number is usually defined as the minimum of the first positive eigenvalue 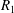$R_{1}$ of an eigenvalue equation for all wavenumber pairs 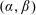$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$, where $\unicode[STIX]{x1D6FC}$ and 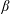$\unicode[STIX]{x1D6FD}$ are the streamwise and spanwise wavenumbers of the normal mode. We prove that 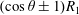$(\cos \unicode[STIX]{x1D703}\pm 1)R_{1}$ are decreasing functions of 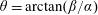$\unicode[STIX]{x1D703}=\arctan (\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D6FC})$ for the parallel flows between no-slip or slip parallel plates with or without variations in temperature. Numerical results inspire us to conjecture that 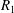$R_{1}$ is also a decreasing function of 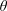$\unicode[STIX]{x1D703}$ for the parallel shear flows under the no-slip boundary condition and without variations in temperature. If the conjecture is correct, the least stable normal modes for the energy stability will be streamwise vortices for these base flows.

JFM classification

Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 881 , 25 December 2019 , pp. 794 - 814
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Busse, F. H. 1969 Bounds on the transport of mass and momentum by turbulent flow between parallel plates. Z. Angew. Math. Phys. 20, 1–14.Google Scholar
Busse, F. H. 1972 A property of the energy stability limit for plane parallel shear flow. Arch. Rat. Mech. Anal. 47, 28–35.Google Scholar
Dongarra, J. J., Straughan, B. & Walker, D. W. 1996 Chebyshev tau-QZ algorithm methods for calculating spectra of hydrodynamic stability problems. Appl. Numer. Maths 22, 399–434.Google Scholar
Joseph, D. D. 1966 Nonlinear stability of the Boussinesq equations by the method of energy. Arch. Rat. Mech. Anal. 22, 163–184.Google Scholar
Joseph, D. D. & Carmi, S. 1969 Stability of Poiseuille flow in pipes, annuli, and channels. Q. Appl. Maths 26, 575–599.Google Scholar
Kaiser, R. & Schmitt, B. J. 2001 Bounds on the energy stability limit of plane parallel shear flows. Z. Angew. Math. Phys. 52, 573–596.Google Scholar
Kingma, D. P. & Ba, J. L.2017 Adam: a method for stochastic optimization. arXiv:1412.6980v9 [cs.LG], 30 Jan 2017.Google Scholar
Knowles, C. P. & Gebhart, B. 1968 The stability of the laminar natural convection boundary layer. J. Fluid Mech. 34, 657–686.Google Scholar
Reddy, S. C. & Henningson, D. S. 1993 Energy growth in viscous channel flows. J. Fluid Mech. 252, 209–238.Google Scholar
Sagalakov, A. M. & Shtern, V. N. 1971 Energy analysis of the stability of plane-parallel flows with an inflection in the velocity profile. J. Appl. Mech. Tech. Phys. 12, 859–864.Google Scholar
Squire, H. B. 1933 On the stability for three-dimensional disturbances of viscous fluid flow between parallel walls. Proc. R. Soc. Lond. A 142, 621–628.Google Scholar
Straughan, B. 1992 The Energy Method, Stability, and Nonlinear Convection. Springer.Google Scholar
Xiong, X. & Tao, J. 2017 Lower bound for transient growth of inclined buoyancy layer. Appl. Math. Mech. Engl. Ed. 38, 779–796.Google Scholar