Article contents
Control of flow around a cylinder by rotary oscillations at a high subcritical Reynolds number
Published online by Cambridge University Press: 18 September 2018
Abstract
We report on a numerical study of the vortex structure modifications and drag reduction in a flow over a rotationally oscillating circular cylinder at a high subcritical Reynolds number, 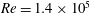 $Re=1.4\times 10^{5}$. Considered are eight forcing frequencies
$Re=1.4\times 10^{5}$. Considered are eight forcing frequencies 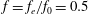 $f=f_{e}/f_{0}=0.5$,
$f=f_{e}/f_{0}=0.5$, 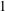 $1$,
$1$, 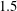 $1.5$,
$1.5$, 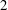 $2$,
$2$, 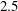 $2.5$,
$2.5$, 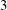 $3$,
$3$, 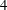 $4$,
$4$, 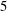 $5$ and three forcing amplitudes
$5$ and three forcing amplitudes 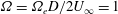 $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}_{e}D/2U_{\infty }=1$,
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}_{e}D/2U_{\infty }=1$, 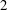 $2$,
$2$, 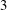 $3$, non-dimensionalized with
$3$, non-dimensionalized with 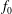 $f_{0}$, which is the natural vortex-shedding frequency without forcing,
$f_{0}$, which is the natural vortex-shedding frequency without forcing, 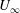 $U_{\infty }$ the free-stream velocity,
$U_{\infty }$ the free-stream velocity, 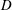 $D$ the diameter of the cylinder. In order to perform a parametric study of a large number of cases (
$D$ the diameter of the cylinder. In order to perform a parametric study of a large number of cases (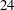 $24$ in total) with affordable computational resources, the three-dimensional unsteady computations were performed using a wall-integrated (WIN) second-moment (Reynolds-stress) Reynolds-averaged Navier–Stokes (RANS) turbulence closure, verified and validated by a dynamic large-eddy simulations (LES) for selected cases (
$24$ in total) with affordable computational resources, the three-dimensional unsteady computations were performed using a wall-integrated (WIN) second-moment (Reynolds-stress) Reynolds-averaged Navier–Stokes (RANS) turbulence closure, verified and validated by a dynamic large-eddy simulations (LES) for selected cases (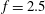 $f=2.5$,
$f=2.5$, 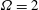 $\unicode[STIX]{x1D6FA}=2$ and
$\unicode[STIX]{x1D6FA}=2$ and 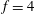 $f=4$,
$f=4$, 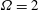 $\unicode[STIX]{x1D6FA}=2$), as well as by the earlier LES and experiments of the flow over a stagnant cylinder at the same
$\unicode[STIX]{x1D6FA}=2$), as well as by the earlier LES and experiments of the flow over a stagnant cylinder at the same 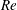 $Re$ number described in Palkin et al. (Flow Turbul. Combust., vol. 97 (4), 2016, pp. 1017–1046). The drag reduction was detected at frequencies equal to and larger than
$Re$ number described in Palkin et al. (Flow Turbul. Combust., vol. 97 (4), 2016, pp. 1017–1046). The drag reduction was detected at frequencies equal to and larger than 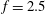 $f=2.5$, while no reduction was observed for the cylinder subjected to oscillations with the natural frequency, even with very different values of the rotation amplitude. The maximum reduction of the drag coefficient is 88 % for the highest tested frequency
$f=2.5$, while no reduction was observed for the cylinder subjected to oscillations with the natural frequency, even with very different values of the rotation amplitude. The maximum reduction of the drag coefficient is 88 % for the highest tested frequency 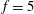 $f=5$ and amplitude
$f=5$ and amplitude 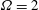 $\unicode[STIX]{x1D6FA}=2$. However, a significant reduction of 78 % appears with the increase of
$\unicode[STIX]{x1D6FA}=2$. However, a significant reduction of 78 % appears with the increase of 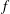 $f$ already for
$f$ already for 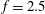 $f=2.5$ and
$f=2.5$ and 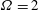 $\unicode[STIX]{x1D6FA}=2$. Such a dramatic reduction in the drag coefficient is the consequence of restructuring of the vortex-shedding topology and a markedly different pressure field featured by a shrinking of the low pressure region behind the cylinder, all dictated by the rotary oscillation. Despite the need to expend energy to force cylinder oscillations, the considered drag reduction mechanism seems a feasible practical option for drag control in some applications for
$\unicode[STIX]{x1D6FA}=2$. Such a dramatic reduction in the drag coefficient is the consequence of restructuring of the vortex-shedding topology and a markedly different pressure field featured by a shrinking of the low pressure region behind the cylinder, all dictated by the rotary oscillation. Despite the need to expend energy to force cylinder oscillations, the considered drag reduction mechanism seems a feasible practical option for drag control in some applications for 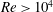 $Re>10^{4}$, since the calculated power expenditure for cylinder oscillation under realistic scenarios is several times smaller than the power saved by the drag reduction.
$Re>10^{4}$, since the calculated power expenditure for cylinder oscillation under realistic scenarios is several times smaller than the power saved by the drag reduction.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 31
- Cited by


