Article contents
Convection due to an unstable density difference across a permeable membrane
Published online by Cambridge University Press: 31 July 2008
Abstract
We study natural convection driven by unstable concentration differences of sodium chloride (NaCl) across a horizontal permeable membrane at Rayleigh numbers (Ra) of 1010 to 1011 and Schmidt number (Sc)=600. A layer of brine lies over a layer of distilled water, separated by the membrane, in square-cross-section tanks. The membrane is permeable enough to allow a small flow across it at higher driving potentials. Based on the predominant mode of transport across the membrane, three regimes of convection, namely an advection regime, a diffusion regime and a combined regime, are identified. The near-membrane flow in all the regimes consists of sheet plumes formed from the unstable layers of fluid near the membrane. In the advection regime observed at higher concentration differences (ΔC) across the membrane, there is a slow overturning through-flow across the membrane; the transport across the membrane occurs mostly by advection. This phenomenology explains the observed Nub~Ra2/Sc scaling of the Nusselt number. The planforms of sheet plumes near the membrane show a dendritic structure due to the combined influence of the mean shear due to the large-scale flow and the entrainment flow of the adjacent plumes. The near-membrane dynamics show initiation, elongation and merger of plumes; a movie is available with the online version of the paper. Increase in Ra results in a larger number of closely and regularly spaced sheet plumes. The mean plume spacing in the advection regime 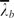 , is larger than the mean plume spacing in Rayleigh–Bénard convection (
, is larger than the mean plume spacing in Rayleigh–Bénard convection (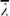 ), and shows a different Ra-dependence. The plume spacings in the advection regime (λb) show a common log-normal probability density function at all Ra. We propose a phenomenology which predicts
), and shows a different Ra-dependence. The plume spacings in the advection regime (λb) show a common log-normal probability density function at all Ra. We propose a phenomenology which predicts 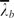 ~
~ 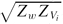 , where Zw and
, where Zw and 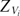 are, respectively, the near-wall length scales in Rayleigh–Bénard convection (RBC) and due to the advection velocity. In the combined regime, which occurs at intermediate values of ΔC, the flux scales as (ΔC/2)4/3. At lower driving potentials, in the diffusion regime, the flux scaling is similar to that in turbulent RBC.
are, respectively, the near-wall length scales in Rayleigh–Bénard convection (RBC) and due to the advection velocity. In the combined regime, which occurs at intermediate values of ΔC, the flux scales as (ΔC/2)4/3. At lower driving potentials, in the diffusion regime, the flux scaling is similar to that in turbulent RBC.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2008
References
REFERENCES
Puthenveettil and Arakeri supplementary movie
Movie 1. The top view of the merging dynamics of sheet plumes shown in figure 10(a). The area in the movie corresponds to the shear-dominated central region in the plan form of figure 8(a). The light green lines in the movie, which form, move and merge, are the top view of the bases of the sheet plumes rising from the membrane surface. Sheet plumes are continuous sheets of rising lighter columns of fluid. The two main dynamics are (a) initiation of plumes in vacant areas and their elongation into sheet plumes and (b) lateral movement and merging of the sheet plumes. The movie corresponds to a Rayleigh number Raw = 5.4 x 1011. A horizontal velocity of the order of W* = 0.48 cm/s is present in the northwest direction. A weak flow of strength Vi = 0.0017 cm/s through the membrane normal to the membrane surface (towards the viewer) is also present. The dark horizontal line has a thickness of 3.2 mm. Other parameters corresponding to the movie are given in table 1.
- 22
- Cited by

