Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liu, Hao
Kolomenskiy, Dmitry
Nakata, Toshiyuki
and
Li, Gen
2017.
Unsteady bio-fluid dynamics in flying and swimming.
Acta Mechanica Sinica,
Vol. 33,
Issue. 4,
p.
663.
Chen, Di
Kolomenskiy, Dmitry
Nakata, Toshiyuki
and
Liu, Hao
2017.
Forewings match the formation of leading-edge vortices and dominate aerodynamic force production in revolving insect wings.
Bioinspiration & Biomimetics,
Vol. 13,
Issue. 1,
p.
016009.
van de Meerendonk, R.
Percin, M.
and
van Oudheusden, B. W.
2018.
Three-dimensional flow and load characteristics of flexible revolving wings.
Experiments in Fluids,
Vol. 59,
Issue. 10,
Jardin, T.
and
Colonius, T.
2018.
On the lift-optimal aspect ratio of a revolving wing at low Reynolds number.
Journal of The Royal Society Interface,
Vol. 15,
Issue. 143,
p.
20170933.
Gourdain, Nicolas
Jardin, Thierry
Serre, Ronan
Prothin, Sébastien
and
Moschetta, Jean-Marc
2018.
Application of a lattice Boltzmann method to some challenges related to micro-air vehicles.
International Journal of Micro Air Vehicles,
Vol. 10,
Issue. 3,
p.
285.
Arranz, Gonzalo
Gonzalo, Alejandro
Uhlmann, Markus
Flores, Oscar
and
García-Villalba, Manuel
2018.
A Numerical Study of the Flow Around a Model Winged Seed in Auto-Rotation.
Flow, Turbulence and Combustion,
Vol. 101,
Issue. 2,
p.
477.
Eldredge, Jeff D.
and
Jones, Anya R.
2019.
Leading-Edge Vortices: Mechanics and Modeling.
Annual Review of Fluid Mechanics,
Vol. 51,
Issue. 1,
p.
75.
Bhat, Shantanu S.
Zhao, Jisheng
Sheridan, John
Hourigan, Kerry
and
Thompson, Mark C.
2019.
Uncoupling the effects of aspect ratio, Reynolds number and Rossby number on a rotating insect-wing planform.
Journal of Fluid Mechanics,
Vol. 859,
Issue. ,
p.
921.
Chen, Long
Zhang, Yanlai
Zhou, Chao
and
Wu, Jianghao
2019.
Aerodynamic mechanisms in bio‐inspired micro air vehicles: a review in the light of novel compound layouts.
IET Cyber-Systems and Robotics,
Vol. 1,
Issue. 1,
p.
2.
Désert, T.
Jardin, T.
Bézard, H.
and
Moschetta, J.M.
2019.
Numerical predictions of low Reynolds number compressible aerodynamics.
Aerospace Science and Technology,
Vol. 92,
Issue. ,
p.
211.
Smith, Luke R.
Jung, Yong Su
Baeder, James D.
and
Jones, Anya R.
2019.
The role of rotary motion on vortices in reverse flow.
Journal of Fluid Mechanics,
Vol. 880,
Issue. ,
p.
723.
Chen, Long
Wu, Jianghao
and
Cheng, Bo
2019.
Volumetric measurement and vorticity dynamics of leading-edge vortex formation on a revolving wing.
Experiments in Fluids,
Vol. 60,
Issue. 1,
Bhat, S. S.
Zhao, J.
Sheridan, J.
Hourigan, K.
and
Thompson, M. C.
2019.
Aspect ratio studies on insect wings.
Physics of Fluids,
Vol. 31,
Issue. 12,
Werner, Nathaniel H.
Chung, Hojae
Wang, Junshi
Liu, Geng
Cimbala, John M.
Dong, Haibo
and
Cheng, Bo
2019.
Radial planetary vorticity tilting in the leading-edge vortex of revolving wings.
Physics of Fluids,
Vol. 31,
Issue. 4,
Chowdhury, Juhi
Cook, Luke
and
Ringuette, Matthew J.
2019.
The Vortex Formation of an Unsteady Translating Plate with a Rotating Tip.
Kirk, Philip B.
and
Jones, Anya R.
2019.
Vortex formation on surging aerofoils with application to reverse flow modelling.
Journal of Fluid Mechanics,
Vol. 859,
Issue. ,
p.
59.
Bhat, Shantanu S.
Zhao, Jisheng
Sheridan, John
Hourigan, Kerry
and
Thompson, Mark C.
2019.
Evolutionary shape optimisation enhances the lift coefficient of rotating wing geometries.
Journal of Fluid Mechanics,
Vol. 868,
Issue. ,
p.
369.
Zhong, Qiang
Dong, Haibo
and
Quinn, Daniel B.
2019.
How dorsal fin sharpness affects swimming speed and economy.
Journal of Fluid Mechanics,
Vol. 878,
Issue. ,
p.
370.
Zhang, Kai
Hayostek, Shelby
Amitay, Michael
He, Wei
Theofilis, Vassilios
and
Taira, Kunihiko
2020.
On the formation of three-dimensional separated flows over wings under tip effects.
Journal of Fluid Mechanics,
Vol. 895,
Issue. ,
Werner, Nathaniel H.
Wang, Junshi
Dong, Haibo
Panah, Azar Eslam
and
Cheng, Bo
2020.
Scaling the vorticity dynamics in the leading-edge vortices of revolving wings with two directional length scales.
Physics of Fluids,
Vol. 32,
Issue. 12,
 $\unicode[STIX]{x1D6FC}$
rotating wing with the Coriolis term being artificially tuned. Reynolds numbers in the range
$\unicode[STIX]{x1D6FC}$
rotating wing with the Coriolis term being artificially tuned. Reynolds numbers in the range
 $Re\in [100;750]$
are considered to identify the interplay between Coriolis and viscous effects. Similarly, artificial tuning of the centrifugal term is achieved to identify the interplay between Coriolis and centrifugal effects. It is shown that (i) the Coriolis effect is the key element in LEV stability for
$Re\in [100;750]$
are considered to identify the interplay between Coriolis and viscous effects. Similarly, artificial tuning of the centrifugal term is achieved to identify the interplay between Coriolis and centrifugal effects. It is shown that (i) the Coriolis effect is the key element in LEV stability for
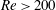 $Re>200$
, (ii) viscous effects are the key element for
$Re>200$
, (ii) viscous effects are the key element for
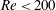 $Re<200$
and (iii) centrifugal effects have a marginal role. The Coriolis effect is found to promote spanwise flow in the core and behind the LEV, which is known to promote outboard vorticity transport and presumably contributes to stabilizing the aft boundary layer. These mechanisms of LEV stabilization have increased authority as
$Re<200$
and (iii) centrifugal effects have a marginal role. The Coriolis effect is found to promote spanwise flow in the core and behind the LEV, which is known to promote outboard vorticity transport and presumably contributes to stabilizing the aft boundary layer. These mechanisms of LEV stabilization have increased authority as
 $\unicode[STIX]{x1D6FC}$
decreases.
$\unicode[STIX]{x1D6FC}$
decreases.