Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Babinsky, Holger
Oorebeek, Joseph
and
Cottingham, Trey
2013.
Corner effects in reflecting oblique shock-wave/boundary-layer interactions.
Loth, Eric
Babinsky, Holger
Titchener, Neil
and
Povinelli, Louis
2013.
A Canonical Normal SBLI Flow Relevant to External Compression Inlets.
Loth, Eric
Titchener, Neil
Babinsky, Holger
and
Povinelli, Louis
2013.
Canonical Normal Shock Wave/Boundary-Layer Interaction Flows Relevant to External Compression Inlets.
AIAA Journal,
Vol. 51,
Issue. 9,
p.
2208.
Webb, N.
Clifford, C.
and
Samimy, M.
2013.
Control of oblique shock wave/boundary layer interactions using plasma actuators.
Experiments in Fluids,
Vol. 54,
Issue. 6,
Titchener, Neil
Babinsky, Holger
and
Loth, Eric
2013.
The Effects of Various Vortex Generator Configurations on a Normal Shock Wave / Boundary Layer Interaction.
Benek, John
Suchyta, Casimir
and
Babinsky, Holger
2013.
The Effect of Tunnel Size on Incident Shock Boundary Layer Interaction Experiments.
Bisek, Nicholas J.
2014.
High-Order Implicit Large-Eddy Simulations of Supersonic Corner Flo.
Eagle, W. Ethan
and
Driscoll, James F.
2014.
Shock wave–boundary layer interactions in rectangular inlets: three-dimensional separation topology and critical points.
Journal of Fluid Mechanics,
Vol. 756,
Issue. ,
p.
328.
Warning, Sally
Turlin, Miranda
Carlson, Lyndel M.
Ligrani, Phillip
and
McQuilling, Mark W.
2014.
Investigation of Shock Wave - Boundary Layer Interactions in a 3.57 Aspect Ratio Wind Tunnel.
Benek, John A.
Suchyta, Casimir J.
and
Babinsky, Holger
2014.
The Effect of Wind Tunnel Size and Shock Strength on Incident Shock Boundary Layer Interaction Experiments.
Bisek, Nicholas J.
2014.
High-Order Implicit Large-Eddy Simulations of a Supersonic Corner Flow over a Compression Ramp.
Campo, Laura M.
and
Eaton, John K.
2015.
Shock boundary layer interactions in a low aspect ratio duct.
International Journal of Heat and Fluid Flow,
Vol. 51,
Issue. ,
p.
353.
Bisek, Nicholas J.
2015.
Sidewall Interaction of a Supersonic Flow over a Compression Ramp.
Leger, Timothy J.
Bisek, Nicholas J.
and
Poggie, Jonathan
2015.
Supersonic Corner Flow Predictions using the Quadratic Constitutive Relation.
Makuni, Tafara E.
Babinsky, Holger
Slaby, Michal
and
Sheaf, Christopher T.
2015.
Shock Wave-Boundary-Layer Interactions in Subsonic Intakes at High Incidence.
Jonathan, Geerts
and
Yu, Kenneth H.
2015.
Corner Flow Separation from Shock Train/Turbulent Boundary-Layer Interactions in Rectangular Isolators.
Wang, Bo
Sandham, Neil D.
Hu, Zhiwei
and
Liu, Weidong
2015.
Numerical study of oblique shock-wave/boundary-layer interaction considering sidewall effects.
Journal of Fluid Mechanics,
Vol. 767,
Issue. ,
p.
526.
Morajkar, Rohan R.
Klomparens, Robin L.
Eagle, W. Ethan
Driscoll, James F.
Gamba, Mirko
and
Benek, John A.
2016.
Relationship Between Intermittent Separation and Vortex Structure in a Three-Dimensional Shock/Boundary-Layer Interaction.
AIAA Journal,
Vol. 54,
Issue. 6,
p.
1862.
Huang, He-Xia
Tan, Hui-Jun
Sun, Shu
and
Ling, Yu
2016.
Evolution of supersonic corner vortex in a hypersonic inlet/isolator model.
Physics of Fluids,
Vol. 28,
Issue. 12,
Leger, Timothy
Bisek, Nicholas
and
Poggie, Jonathan
2016.
Supersonic Corner Flow Predictions Using the Quadratic Constitutive Relation.
AIAA Journal,
Vol. 54,
Issue. 7,
p.
2077.
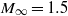 normal shock in a rectangular channel. The ensuing shock wave interaction with the boundary layer on the wind tunnel floor and in the corners was studied using laser Doppler anemometry, Pitot probe traverses, pressure sensitive paint and flow visualization. The primary mechanism explaining the link between the corner separation size and the other areas of separation appears to be the generation of compression waves at the corner, which act to smear the adverse pressure gradient imposed upon other parts of the flow. Experimental results indicate that the alteration of the
normal shock in a rectangular channel. The ensuing shock wave interaction with the boundary layer on the wind tunnel floor and in the corners was studied using laser Doppler anemometry, Pitot probe traverses, pressure sensitive paint and flow visualization. The primary mechanism explaining the link between the corner separation size and the other areas of separation appears to be the generation of compression waves at the corner, which act to smear the adverse pressure gradient imposed upon other parts of the flow. Experimental results indicate that the alteration of the 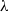 -region, which occurs in the supersonic portion of the shock wave/boundary layer interaction (SBLI), is more important than the generation of any blockage in the subsonic region downstream of the shock wave.
-region, which occurs in the supersonic portion of the shock wave/boundary layer interaction (SBLI), is more important than the generation of any blockage in the subsonic region downstream of the shock wave.
