Article contents
Critical slope for laminar transcritical shallow-water flows
Published online by Cambridge University Press: 13 October 2015
Abstract
Backwater curves denote the depth profiles of steady flows in a shallow open channel. The classification of these curves for turbulent regimes is commonly used in hydraulics. When the bottom slope 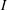 $I$ is increased, they can describe the transition from fluvial to torrential regimes. In the case of an infinitely wide channel, we show that laminar flows have the same critical height
$I$ is increased, they can describe the transition from fluvial to torrential regimes. In the case of an infinitely wide channel, we show that laminar flows have the same critical height 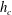 $h_{c}$ as that in the turbulent case. This feature is due to the existence of surface slope singularities associated to plug-like velocity profiles with vanishing boundary-layer thickness. We also provide the expression of the critical surface slope as a function of the bottom curvature at the critical location. These results validate a similarity model to approximate the asymptotic Navier–Stokes equations for small slopes
$h_{c}$ as that in the turbulent case. This feature is due to the existence of surface slope singularities associated to plug-like velocity profiles with vanishing boundary-layer thickness. We also provide the expression of the critical surface slope as a function of the bottom curvature at the critical location. These results validate a similarity model to approximate the asymptotic Navier–Stokes equations for small slopes 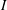 $I$ with Reynolds number
$I$ with Reynolds number 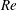 $Re$ such that
$Re$ such that 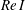 $Re\,I$ is of order 1.
$Re\,I$ is of order 1.
- Type
- Rapids
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 2
- Cited by



