Published online by Cambridge University Press: 12 October 2011
A new experimental investigation of decaying turbulence generated by a low-blockage space-filling fractal square grid is presented. We find agreement with previous works by Seoud & Vassilicos (Phys. Fluids, vol. 19, 2007, 105108) and Mazellier & Vassilicos (Phys. Fluids, vol. 22, 2010, 075101) but also extend the length of the assessed decay region and consolidate the results by repeating the experiments with different probes of increased spatial resolution. It is confirmed that this moderately high Reynolds number 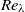 turbulence (up to
turbulence (up to 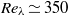 here) does not follow the classical high Reynolds number scaling of the dissipation rate
here) does not follow the classical high Reynolds number scaling of the dissipation rate 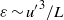 and does not obey the equivalent proportionality between the Taylor-based Reynolds number
and does not obey the equivalent proportionality between the Taylor-based Reynolds number  and the ratio of integral scale
and the ratio of integral scale 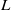 to the Taylor microscale
to the Taylor microscale 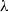 . Instead we observe an approximate proportionality between
. Instead we observe an approximate proportionality between 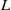 and
and 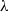 during decay. This non-classical behaviour is investigated by studying how the energy spectra evolve during decay and examining how well they can be described by self-preserving single-length-scale forms. A detailed study of homogeneity and isotropy is also presented which reveals the presence of transverse energy transport and pressure transport in the part of the turbulence decay region where we take data (even though previous studies found mean flow and turbulence intensity profiles to be approximately homogeneous in much of the decay region). The exceptionally fast turbulence decay observed in the part of the decay region where we take data is consistent with the non-classical behaviour of the dissipation rate. Measurements with a regular square mesh grid as well as comparisons with active-grid experiments by Mydlarski & Warhaft (J. Fluid Mech., vol. 320, 1996, pp. 331–368) and Kang, Chester & Meveneau (J. Fluid Mech., vol. 480, 2003, pp. 129–160) are also presented to highlight the similarities and differences between these turbulent flows and the turbulence generated by our fractal square grid.
during decay. This non-classical behaviour is investigated by studying how the energy spectra evolve during decay and examining how well they can be described by self-preserving single-length-scale forms. A detailed study of homogeneity and isotropy is also presented which reveals the presence of transverse energy transport and pressure transport in the part of the turbulence decay region where we take data (even though previous studies found mean flow and turbulence intensity profiles to be approximately homogeneous in much of the decay region). The exceptionally fast turbulence decay observed in the part of the decay region where we take data is consistent with the non-classical behaviour of the dissipation rate. Measurements with a regular square mesh grid as well as comparisons with active-grid experiments by Mydlarski & Warhaft (J. Fluid Mech., vol. 320, 1996, pp. 331–368) and Kang, Chester & Meveneau (J. Fluid Mech., vol. 480, 2003, pp. 129–160) are also presented to highlight the similarities and differences between these turbulent flows and the turbulence generated by our fractal square grid.