Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rodríguez-López, Eduardo
Bruce, Paul J. K.
and
Buxton, Oliver R. H.
2017.
Flow characteristics and scaling past highly porous wall-mounted fences.
Physics of Fluids,
Vol. 29,
Issue. 7,
Diwan, Sourabh S.
and
Morrison, Jonathan F.
2017.
Spectral structure and linear mechanisms in a rapidly distorted boundary layer.
International Journal of Heat and Fluid Flow,
Vol. 67,
Issue. ,
p.
63.
Sessa, Vincenzo
Xie, Zheng-Tong
and
Herring, Steven
2018.
Turbulence and dispersion below and above the interface of the internal and the external boundary layers.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 182,
Issue. ,
p.
189.
Ismail, Umair
Zaki, Tamer A.
and
Durbin, Paul A.
2018.
Simulations of rib-roughened rough-to-smooth turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 843,
Issue. ,
p.
419.
Pillai, Aditya
and
Prasad, B.V.S.S.S.
2018.
Effect of wall surface roughness on condensation shock.
International Journal of Thermal Sciences,
Vol. 132,
Issue. ,
p.
435.
Placidi, M.
and
Ganapathisubramani, B.
2018.
Turbulent Flow Over Large Roughness Elements: Effect of Frontal and Plan Solidity on Turbulence Statistics and Structure.
Boundary-Layer Meteorology,
Vol. 167,
Issue. 1,
p.
99.
Ismail, Umair
Zaki, Tamer A.
and
Durbin, Paul A.
2018.
The effect of cube-roughened walls on the response of rough-to-smooth (RTS) turbulent channel flows.
International Journal of Heat and Fluid Flow,
Vol. 72,
Issue. ,
p.
174.
Chung, D.
Monty, J. P.
and
Hutchins, N.
2018.
Similarity and structure of wall turbulence with lateral wall shear stress variations.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
p.
591.
Vanderwel, Christina
and
Ganapathisubramani, Bharathram
2019.
Turbulent Boundary Layers Over Multiscale Rough Patches.
Boundary-Layer Meteorology,
Vol. 172,
Issue. 1,
p.
1.
Rouhi, Amirreza
Chung, Daniel
and
Hutchins, Nicholas
2019.
Direct numerical simulation of open-channel flow over smooth-to-rough and rough-to-smooth step changes.
Journal of Fluid Mechanics,
Vol. 866,
Issue. ,
p.
450.
Rouhi, Amirreza
Chung, Daniel
and
Hutchins, Nicholas
2019.
Progress in Turbulence VIII.
Vol. 226,
Issue. ,
p.
81.
Li, Mogeng
de Silva, Charitha M.
Rouhi, Amirreza
Baidya, Rio
Chung, Daniel
Marusic, Ivan
and
Hutchins, Nicholas
2019.
Recovery of wall-shear stress to equilibrium flow conditions after a rough-to-smooth step change in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
472.
Mahananda, Minakshee
Hanmaiahgari, Prashanth Reddy
and
Balachandar, Ram
2020.
Advanced Numerical Methods in Foundation Engineering.
p.
133.
Ghaisas, Niranjan S.
2020.
A Predictive Analytical Model for Surface Shear Stresses and Velocity Profiles Behind a Surface Roughness Jump.
Boundary-Layer Meteorology,
Vol. 176,
Issue. 3,
p.
349.
Sessa, Vincenzo
Xie, Zheng-Tong
and
Herring, Steven
2020.
Thermal Stratification Effects on Turbulence and Dispersion in Internal and External Boundary Layers.
Boundary-Layer Meteorology,
Vol. 176,
Issue. 1,
p.
61.
Van Buren, T.
Floryan, D.
Ding, L.
Hellström, L. H. O.
and
Smits, A. J.
2020.
Turbulent pipe flow response to a step change in surface roughness.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Forooghi, Pourya
Yang, Xiang I. A.
and
Abkar, Mahdi
2020.
Roughness-induced secondary flows in stably stratified turbulent boundary layers.
Physics of Fluids,
Vol. 32,
Issue. 10,
Li, Mogeng
de Silva, Charitha M.
Chung, Daniel
Pullin, Dale I.
Marusic, Ivan
and
Hutchins, Nicholas
2021.
Experimental study of a turbulent boundary layer with a rough-to-smooth change in surface conditions at high Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 923,
Issue. ,
Zhang, Wen
Wan, Minping
Xia, Zhenhua
Wang, Jianchun
Lu, Xiyun
and
Chen, Shiyi
2021.
Constrained large-eddy simulation of turbulent flow over inhomogeneous rough surfaces.
Theoretical and Applied Mechanics Letters,
Vol. 11,
Issue. 1,
p.
100229.
Ding, Liuyang
and
Smits, Alexander J.
2021.
Relaxation of turbulent pipe flow downstream of a square bar roughness element.
Journal of Fluid Mechanics,
Vol. 922,
Issue. ,
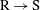 $\text{R}\rightarrow \text{S}$) is examined. Measurements of the flow were made by hot wires, whereas the friction velocity was estimated by Preston tube measurements. By means of a diagnostic plot of the turbulence intensity, it is shown that above the internal layer the flow exhibits characteristics of a rough, wall-bounded flow, whereas near the wall the turbulence intensity is similar to that of an isolated smooth wall. Similarly, viscous scaling of the mean streamwise velocity shows an excessive wake region downstream of the
$\text{R}\rightarrow \text{S}$) is examined. Measurements of the flow were made by hot wires, whereas the friction velocity was estimated by Preston tube measurements. By means of a diagnostic plot of the turbulence intensity, it is shown that above the internal layer the flow exhibits characteristics of a rough, wall-bounded flow, whereas near the wall the turbulence intensity is similar to that of an isolated smooth wall. Similarly, viscous scaling of the mean streamwise velocity shows an excessive wake region downstream of the 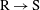 $\text{R}\rightarrow \text{S}$ wall surface change that diminishes with the fetch from the surface change. Above the internal layer a second peak in the streamwise Reynolds stress was associated with the upstream rough-wall flow. Examination of the turbulent spectra revealed the presence of large-scale motions within this region that gradually diminish in strength with increasing distance from the change in surface roughness. The magnitude of the near-wall peak failed to collapse to that of a comparable smooth-wall boundary layer under viscous scaling, however, the wall-normal location of the peak appears to be at
$\text{R}\rightarrow \text{S}$ wall surface change that diminishes with the fetch from the surface change. Above the internal layer a second peak in the streamwise Reynolds stress was associated with the upstream rough-wall flow. Examination of the turbulent spectra revealed the presence of large-scale motions within this region that gradually diminish in strength with increasing distance from the change in surface roughness. The magnitude of the near-wall peak failed to collapse to that of a comparable smooth-wall boundary layer under viscous scaling, however, the wall-normal location of the peak appears to be at 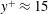 $y^{+}\approx 15$ at all downstream distances. A new mixed scaling is proposed for the near-wall peak based on the corrected wake deficit and the friction velocity. This shows the importance of outer region to the growth of near-wall peak in this non-equilibrium boundary layer.
$y^{+}\approx 15$ at all downstream distances. A new mixed scaling is proposed for the near-wall peak based on the corrected wake deficit and the friction velocity. This shows the importance of outer region to the growth of near-wall peak in this non-equilibrium boundary layer.