Article contents
Diapycnal mixing of passive tracers by Kelvin–Helmholtz instabilities
Published online by Cambridge University Press: 11 August 2020
Abstract
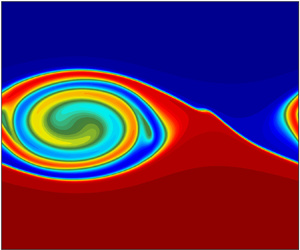
This paper considers the diapycnal transport of passive tracers during a Kelvin–Helmholtz mixing event. Numerical simulations of a traditional Kelvin–Helmholtz (KH) configuration of a stratified shear flow are extended to include layers of passive tracer at different locations relative to the shear layer. The evolution of the tracers during the simulation is followed and is analysed using different theoretical approaches. One is to consider the evolution via the distribution in density–tracer space which clearly reveals how the tracers are redistributed across isopycnals by the mixing driven by the growing and saturating KH billow. The shape of the distribution places constraints on the redistribution of the tracer and, for this problem of symmetrically stratified shear, it is shown that the distribution typically tends to a compact form, with significant regions that are nearly linear. The redistribution across isopycnals is also considered via a diffusion equation for the tracer relative to coordinates based on the geometry of density surfaces. The equation is a generalisation of an equation previously derived for transport of density in these coordinates and includes an extra eddy term that arises because there is variation of the tracer along density surfaces. Under certain circumstances and at later stages of the flow, the eddy term can be neglected, and the evolution of the mean tracer profile can be adequately represented using a simple diffusion equation where diffusivity is defined as the effective diffusivity of density, scaled by the molecular diffusion of the tracer.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 8
- Cited by

