Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T06:48:56.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of a turbulent flow in a rotating channel with a sudden expansion

Published online by Cambridge University Press:  17 March 2014

Eric Lamballais
Eric Lamballais*
Affiliation:
Department of Fluid Flow, Heat Transfer and Combustion, Institut PPrime, CNRS – Université de Poitiers – ENSMA, Téléport 2, Boulevard Marie et Pierre Curie, B.P. 30179, 86962 Futuroscope Chasseneuil CEDEX, France
*
†Email address for correspondence: eric.lamballais@univ-poitiers.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The effects of spanwise rotation on the channel flow across a symmetric sudden expansion are investigated using direct numerical simulation. Four rotation regimes are considered with the same Reynolds number 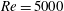$\mathit{Re}=5000$ and expansion ratio 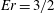$\mathit{Er}=3/2$. Upstream from the expansion, inflow turbulent conditions are generated realistically for each rotation rate through a very simple and efficient technique of recycling without the need for any precursor calculation. As the rotation is increased, the flow becomes progressively asymmetric with stabilization (destabilization) effects on the cyclonic (anticyclonic) side, respectively. These rotation effects, already present in the upstream channel, lead further downstream to an increase (reduction) of the separation size behind the cyclonic (anticyclonic) step. In the cyclonic separation, the free-shear layer created behind the step corner leads to the formation of large-scale spanwise vortices that become increasingly two-dimensional as the rotation is increased. Conversely, in the anticyclonic region, the turbulent structures in the separated layer are more elongated in the streamwise direction and also more active in promoting reattachment. For the highest rotation rate, a secondary separation is observed further downstream in the anticyclonic region, leading to the establishment of an elongated recirculation bubble that deflects the main flow towards the cyclonic wall. The highest level of turbulent kinetic energy is obtained at high rotation near the cyclonic reattachment in a region where stabilization effects are expected. The phenomenological model of absolute vortex stretching is found to be useful in understanding how the rotation influences the dynamics in the various regions of the flow.

JFM classification

Turbulent Flows: Rotating turbulence Wakes/Jets: Separated flows Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 745 , 25 April 2014 , pp. 92 - 131
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbott, D. E. & Kline, S. J. 1962 Experimental investigation of subsonic turbulent flow over single and double backward facing steps. Trans. ASME: J. Basic Engng 84 (3), 317–325.CrossRefGoogle Scholar
del Alamo, J. C. & Jimenez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
Alfredsson, P. H. & Persson, H. 1989 Instabilities in channel flow with system rotation. J. Fluid Mech. 202, 543–557.Google Scholar
Barri, M. & Andersson, H. I. 2010a Computer experiments on rapidly rotating plane Couette flow. Commun. Comput. Phys. 7 (4), 683–717.Google Scholar
Barri, M. & Andersson, H. I. 2010b Turbulent flow over a backward-facing step. Part 1. Effects of anti-cyclonic system rotation. J. Fluid Mech. 665, 382–417.Google Scholar
Barri, M., El Khoury, G. K., Andersson, H. I. & Pettersen, B. 2009a DNS of backward-facing step flow with fully turbulent inflow. Intl J. Numer. Meth. Fluids 64, 777–792.CrossRefGoogle Scholar
Barri, M., El Khoury, G. K., Andersson, H. I. & Pettersen, B. 2009b Inflow conditions for inhomogeneous turbulent flows. Intl J. Numer. Meth. Fluids 60, 227–235.Google Scholar
Bech, K. H. & Andersson, H. I. 1997 Turbulent plane Couette flow subject to strong system rotation. J. Fluid Mech. 347, 289–314.Google Scholar
Biau, D. & Bottaro, A. 2004 Transient growth and minimal defects: two possible initial paths of transition to turbulence in plane shear flows. Phys. Fluids 16 (10), 3515–3529.Google Scholar
Bidokhti, A. A. & Tritton, D. J. 1992 The structure of a turbulent free shear layer in a rotating fluid. J. Fluid Mech. 241, 469–502.Google Scholar
Bradshaw, B. 1969 The analogy between streamline curvature and buoyancy in turbulent shear flow. J. Fluid Mech. 36, 177–191.Google Scholar
Brethouwer, G. 2005 The effect of rotation on rapidly sheared homogeneous turbulence and passive scalar transport. Linear theory and direct numerical simulation. J. Fluid Mech. 542, 305–342.Google Scholar
Brethouwer, G., Schlatter, P. & Johansson, A. V. 2011 Turbulence, instabilities and passive scalars in rotating channel flow. J. Phys.: Conf. Ser. 318, 032025.Google Scholar
Buell, J. C. & Huerre, P. 1988 Inflow/outflow boundary conditions and global dynamics of spatial mixing layers. In Studying Turbulence Using Numerical Simulation Databases, 2. Proceedings of the 1988 Summer Program, Stanford University (SEE N89-24538 18-34) pp. 19–27.Google Scholar
Cambon, C., Benoit, J. P., Shao, L. & Jacquin, L. 1994 Stability analysis and large-eddy simulation of rotating turbulence with organized eddies. J. Fluid Mech. 278, 175–200.Google Scholar
Comte-Bellot, G. 1965 Ecoulement turbulent entre deux paroi parallèles. Documentation Scientifique et Technique de l’Armement 419. Publications Scientifiques et Techniques du Ministère de l’Air.Google Scholar
Deardorff, J. W. 1970 A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 41, 453–480.Google Scholar
Grundestam, O., Wallin, S. & Johansson, A. V. 2008 Direct numerical simulations of rotating turbulent channel flow. J. Fluid Mech. 598, 177–199.Google Scholar
Hamba, F. 2006 The mechanism of zero mean absolute vorticity state in rotating channel flow. Phys. Fluids 18, 125104.Google Scholar
Hart, J. E. 1971 Instability and secondary motion in a rotating channel flow. J. Fluid Mech. 45, 341–351.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.Google Scholar
Iwamoto, K., Suzuki, Y. & Kasagi, N. 2002 Reynolds number effect on wall turbulence: toward effective feedback control. Intl J. Heat Fluid Flow 23 (5), 678–689.Google Scholar
Jiménez, J. 1990 Transition to turbulence in two-dimensional Poiseuille flow. J. Fluid Mech. 218, 265–297.Google Scholar
Johnson, J. A. 1963 The stability of shearing motion in a rotating fluid. J. Fluid Mech. 17 (3), 337–352.Google Scholar
Johnston, J. P., Halleen, R. M. & Lezius, D. K. 1972 Effects of spanwise rotation on the structure of two-dimensional fully developed turbulent channel flow. J. Fluid Mech. 56, 533–557.Google Scholar
Khaledi, H. A., Barri, M. & Andersson, H. I. 2009 On the stabilizing effect of the Coriolis force on the turbulent wake of a normal plate. Phys. Fluids 21, 095104.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kravchenko, A. G. & Moin, P. 1997 On the effect of numerical errors in large eddy simulation of turbulent flows. J. Comput. Phys. 131, 310–322.Google Scholar
Kristoffersen, R. & Andersson, H. I. 1993 Direct simulations of low-Reynolds-number turbulent flow in rotating channel. J. Fluid Mech. 256, 163–197.Google Scholar
Laizet, S. & Lamballais, E. 2009 High-order compact schemes for incompressible flows: a simple and efficient method with quasi-spectral accuracy. J. Comput. Phys. 228, 5989–6015.Google Scholar
Laizet, S., Lamballais, E. & Vassilicos, J. C. 2010 A numerical strategy to combine high-order schemes, complex geometry and parallel computing for high resolution DNS of fractal generated turbulence. Comput. Fluids 39 (3), 471–484.Google Scholar
Laizet, S. & Li, N. 2011 Incompact3d: a powerful tool to tackle turbulence problems with up to $o(10^5)$ computational cores. Intl J. Numer. Meth. Fluids 67 (11), 1735–1757.Google Scholar
Lamballais, E., Fortuné, V. & Laizet, S. 2011 Straightforward high-order numerical dissipation via the viscous term for direct and large eddy simulation. J. Comput. Phys. 230, 3270–3275.Google Scholar
Lamballais, E., Lesieur, M. & Métais, O. 1996a Effects of spanwise rotation on the vorticity stretching in transitional and turbulent channel flow. Intl J. Heat Fluid Flow 17 (3), 324–332.Google Scholar
Lamballais, E., Lesieur, M. & Métais, O. 1996b Influence of a solid-body rotation upon coherent vortices in a channel. C. R. Acad. Sci. Paris II B 323, 95–101.Google Scholar
Lamballais, E., Métais, O. & Lesieur, M. 1998 Spectral-dynamic model for large-eddy simulations of turbulent rotating channel flow. Theor. Comput. Fluid Dyn. 12, 149–177.Google Scholar
Le, H., Moin, P. & Kim, J. 1997 Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 330, 349–374.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.Google Scholar
Lesieur, M. 2008 Turbulence in Fluids. 4th edn. Springer.Google Scholar
Lesieur, M., Yanase, S. & Métais, O. 1991 Stabilizing and destabilizing effects of a solid-body rotation on quasi-two-dimensional shear layers. Phys. Fluids 3, 403–407.Google Scholar
Lezius, D. K. & Johnston, J. P. 1976 Roll-cell instabilities in rotating laminar and turbulent channel flows. J. Fluid Mech. 77, 153–175.Google Scholar
Lund, T. S., Wu, X. & Squires, K. D. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 140, 233–258.Google Scholar
Métais, O., Flores, C., Yanase, S., Riley, J. J. & Lesieur, M. 1995 Rotating free shear flows. Part 2: Numerical simulations. J. Fluid Mech. 293, 41–80.Google Scholar
Métais, O., Yanase, S., Flores, C., Bartello, P. & Lesieur, M. 1993 Reorganization of coherent vortices in shear layers under the action of solid-body rotation. In Turbulent Shear Flows VIII, pp. 415–430.Google Scholar
Mizushima, J. & Shiotani, Y. 2000 Structural instability of the bifurcation diagram for two-dimensional flow in a channel with a sudden expansion. J. Fluid Mech. 420, 131–145.Google Scholar
Moin, P. & Kim, J. 1982 Numerical investigation of turbulent channel flow. J. Fluid Mech. 118, 341–377.Google Scholar
Oberlack, M. 2001 A unified approach for symmetries in plane parallel turbulent shear flows. J. Fluid Mech. 427, 299–328.Google Scholar
Ol’shanskii, M. A. & Staroverov, V. M. 2000 On simulation of outflow boundary conditions in finite difference calculations for incompressible fluid. Intl J. Numer. Meth. Fluids 33 (4), 499–534.Google Scholar
Orszag, S. A. 1971 Accurate solution of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50, 689–703.Google Scholar
Parnaudeau, P., Carlier, J., Heitz, D. & Lamballais, E. 2008 Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys. Fluids 20, 085101.Google Scholar
Parnaudeau, P., Lamballais, E., Heitz, D. & Silvestrini, J. H. 2004 Combination of the immersed boundary method with compact schemes for DNS of flows in complex geometry. In Direct and Large-Eddy Simulation V (ed. Friedrich, R., Geurts, B. J. & Métais, O.), ERCOFTAC Series, Vol. 9, pp. 581–590. Kluwer Academic.Google Scholar
Pedley, T. J. 1969 On the instability of viscous flow in a rapidly rotating pipe. J. Fluid Mech. 35, 97–115.Google Scholar
Rothe, P. H. & Johnston, I. P. 1979 Free shear layer behavior in rotating systems. Trans. ASME: J. Fluids Engng 101, 117–120.Google Scholar
Salhi, A. & Cambon, C. 1997 An analysis of rotating shear flow using linear theory and DNS and LES results. J. Fluid Mech. 347, 171–195.Google Scholar
Schäfer, F., Breuer, M. & Durst, F. 2009 The dynamics of the transitional flow over a backward-facing step. J. Fluid Mech. 623, 85–119.Google Scholar
Smyth, R. 1979 Turbulent flow over a plane symmetric sudden expansion. Trans. ASME: J. Fluids Engng 101, 348–353.Google Scholar
Tanaka, M., Kida, S., Yanase, S. & Kawahara, G. 2000 Zero-absolute-vorticity state in a rotating turbulent shear flow. Phys. Fluids 12 (8), 1979–1985.Google Scholar
Tanaka, M., Yanase, S., Kida, S. & Kawahara, G. 1998 Vortical structures in rotating uniformly sheared turbulence. Flow Turbul. Combust. 60, 301–332.Google Scholar
Tritton, D. J. 1992 Stabilization and destabilization of turbulent shear flow in a rotating fluid. J. Fluid Mech. 241, 503–523.Google Scholar
Tritton, D. J. & Davies, P. A. 1981 Instabilities in geophysical fluid dynamics. In Hydrodynamic Instabilities and the Transition to Turbulence (ed. Swinney, H. L. & Gollub, J. P.), Springer.Google Scholar
Vissher, J. & Andersson, H. I. 2011 Particle image velocimetry measurements of massively separated turbulent flows with rotation. Phys. Fluids 23, 075108.Google Scholar
Witt, H. T. & Joubert, P. N.1985 Effect of rotation on a turbulent wake. In Symposium on Turbulent Shear Flows, 5th, Ithaca, NY, August 7–9.Google Scholar
Yanase, S., Flores, C., Métais, O. & Riley, J. J. 1993 Rotating free-shear flows. I. Linear stability analysis. Phys. Fluids 5 (11), 2725–2737.Google Scholar
Yanase, S., Tanaka, M., Kida, S. & Kawahara, G. 2004 Generation and sustenance mechanisms of coherent vortical structures in rotating shear turbulence of zero-mean-absolute vorticity. Fluid Dyn. Res. 35 (4), 237–254.Google Scholar