Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T17:35:41.578Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of backward-facing step flow at $Re_{\unicode[STIX]{x1D70F}}=395$ and expansion ratio 2

Published online by Cambridge University Press:  24 January 2019

A. Pont-Vílchez Open the ORCID record for A. Pont-Vílchez [Opens in a new window] ,
F. X. Trias Open the ORCID record for F. X. Trias [Opens in a new window] ,
A. Gorobets Open the ORCID record for A. Gorobets [Opens in a new window]  and
A. Oliva Open the ORCID record for A. Oliva [Opens in a new window]
A. Pont-Vílchez*
Affiliation:
Heat and Mass Transfer Technological Centre (CTTC), Universitat Politècnica de Catalunya BARCELONA Tech (UPC) C/ Colom, 11 08222 Terrassa (Barcelona), Spain
F. X. Trias
Affiliation:
Heat and Mass Transfer Technological Centre (CTTC), Universitat Politècnica de Catalunya BARCELONA Tech (UPC) C/ Colom, 11 08222 Terrassa (Barcelona), Spain
A. Gorobets
Affiliation:
Keldysh Institute of Applied Mathematics, 4A, Miusskaya Sq., Moscow 125047, Russia
A. Oliva
Affiliation:
Heat and Mass Transfer Technological Centre (CTTC), Universitat Politècnica de Catalunya BARCELONA Tech (UPC) C/ Colom, 11 08222 Terrassa (Barcelona), Spain
*
†Email address for correspondence: arnau@cttc.upc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Backward-facing step (BFS) constitutes a canonical configuration to study wall-bounded flows subject to massive expansions produced by abrupt changes in geometry. Recirculation flow regions are common in this type of flow, driving the separated flow to its downstream reattachment. Consequently, strong adverse pressure gradients arise through this process, feeding flow instabilities. Therefore, both phenomena are strongly correlated as the recirculation bubble shape defines how the flow is expanded, and how the pressure rises. In an incompressible flow, this shape depends on the Reynolds value and the expansion ratio. The influence of these two variables on the bubble length is widely studied, presenting an asymptotic behaviour when both parameters are beyond a certain threshold. This is the usual operating point of many practical applications, such as in aeronautical and environmental engineering. Several numerical and experimental studies have been carried out regarding this topic. The existing simulations considering cases beyond the above-mentioned threshold have only been achieved through turbulence modelling, whereas direct numerical simulations (DNS) have been performed only at low Reynolds numbers. Hence, despite the great importance of achieving this threshold, there is a lack of reliable numerical data to assess the accuracy of turbulence models. 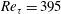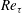In this context, a DNS of an incompressible flow over a BFS is presented in this paper, considering a friction Reynolds number ($Re_{\unicode[STIX]{x1D70F}}$) of 395 at the inflow and an expansion ratio 2. Finally, the elongation of the Kelvin–Helmholtz instabilities along the shear layer is also studied.

JFM classification

Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 341 - 363
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Armaly, B. F., Durst, F., Pereira, J. C. F. & Schonung, B. 1983 Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 127, 473–496.10.1017/S0022112083002839Google Scholar
Barri, M., El Khoury, G. K., Andersson, H. I. & Pettersen, B. 2009 Inflow conditions for inhomogeneous turbulent flows. Intl J. Numer. Meth. Fluids 60 (2), 227–235.10.1002/fld.1884Google Scholar
Barri, M., El Khoury, G. K., Andersson, H. I. & Pettersen, B. 2010 DNS of backward-facing step flow with fully turbulent inflow. Intl J. Numer. Meth. Fluids 64 (7), 777–792.Google Scholar
Biswas, G., Breuer, M. & Durst, F. 2004 Backward-facing step flows for various expansion ratios at low and moderate Reynolds numbers. Trans. ASME J. Fluids Engng 126 (3), 362–374.10.1115/1.1760532Google Scholar
Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Math. Comput. 22, 745–762.10.1090/S0025-5718-1968-0242392-2Google Scholar
De Brederode, V. & Bradshaw, P.1972 Three-dimensional flow in nominally two-dimensional separation bubbles. I. Flow behind a rearward-facing step. Tech. Rep., IC Aero Rep 72-19, Imperial College, London.Google Scholar
Driver, D. M. & Seegmiller, H. L. 1985 Features of a reattaching turbulent shear layer in divergent channel flow. AIAA J. 23 (2), 163–171.10.2514/3.8890Google Scholar
Durst, F. & Tropea, C. 1981 Turbulent backward-facing step flows in two-dimensional ducts and channels. In Proceedings of Turbulent Shear Flows, 3, Symposium, University of California, Davis, pp. 18.1–18.5.Google Scholar
Eaton, J. K. & Johnston, J. P.1980 Turbulent flow reattachment: an experimental study of the flow and structure behind a backward facing step. Rep. MD-39, Dept of Mech Engng, Stanford University, Stanford, CA.Google Scholar
Gorobets, A., Trias, F. X. & Oliva, A. 2013 A parallel MPI+OpenMP+OpenCL algorithm for hybrid supercomputations of incompressible flows. Comput. Fluids 88, 764–772.10.1016/j.compfluid.2013.05.021Google Scholar
Gritskevich, M. S., Garbaruk, A. V., Schütze, J. & Menter, F. R. 2012 Development of DDES and IDDES formulations for the k-𝜔 shear stress transport model. Flow Turbul. Combust. 88 (3), 431–449.10.1007/s10494-011-9378-4Google Scholar
Jovic, S. & Driver, D.1994 Backward-facing step measurements at low Reynolds number, $Reh=5000$ . Nasa Tech. Mem. (February).Google Scholar
Jovic, S. & Driver, D. 1995 Reynolds number effect on the skin friction in separated flows behind a backward-facing step. Exp. Fluids 18 (6), 464–467.10.1007/BF00208471Google Scholar
Kasagi, N. & Matsunaga, A. 1995 Three-dimensional particle-tracking velocimetry measurement of turbulence statistics and energy budget in a backward-facing step flow. Intl J. Heat Fluid Flow 16 (6), 477–485.10.1016/0142-727X(95)00041-NGoogle Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 123, 308–323.10.1016/0021-9991(85)90148-2Google Scholar
Kostas, J., Soria, J. & Chong, M. 2002 Particle image velocimetry measurements of a backward-facing step flow. Exp. Fluids 33 (6), 838–853.10.1007/s00348-002-0521-9Google Scholar
Kuehn, D. M. 1980 Effects of adverse pressure gradient on the incompressible reattaching flow over a rearward-facing step. AIAA J. 18 (3), 343–344.10.2514/3.50765Google Scholar
Lasher, W. C. & Taulbee, D. B. 1992 On the computation of turbulent backstep flow. Intl J. Heat Fluid Flow 13 (1), 30–40.10.1016/0142-727X(92)90057-GGoogle Scholar
Le, H., Moin, P. & Kim, J. 1997 Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 330, 349–374.10.1017/S0022112096003941Google Scholar
Meri, A. & Wengle, H. 2002 DNS and LES of turbulent backward-facing step flow using 2nd-and 4th-order discretization. In Advances in LES of Complex Flows (ed. Friedrich, R. & Rodi, W.), Fluid Mechanics and its Applications, vol. 65, pp. 99–114. Kluwer.10.1007/0-306-48383-1_7Google Scholar
Mockett, C., Haase, W. & Schwamborn, D. 2018 Go4Hybrid: Grey Area Mitigation for Hybrid RANS-LES Methods, Notes on Numerical Fluid Mechanics and Multidisciplinary Design, vol. 134. Springer.10.1007/978-3-319-52995-0Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11, 943–945.10.1063/1.869966Google Scholar
Nadge, P. M. & Govardhan, R. N. 2014 High Reynolds number flow over a backward-facing step: structure of the mean separation bubble. Exp. Fluids 55 (1), 1657–1678.10.1007/s00348-013-1657-5Google Scholar
Ötügen, M. V. 1991 Expansion ratio effects on the separated shear layer and reattachment downstream of a backward-facing step. Exp. Fluids 10 (5), 273–280.10.1007/BF00202460Google Scholar
Pont-Vílchez, A., Trias, F. X., Gorobets, A. & Oliva, A.2018 Direct numerical simulation results presented in this paper. http://www.cttc.upc.edu/downloads/BFS_Ret395_ER2.Google Scholar
Schäfer, F., Breuer, M. & Durst, F. 2009 The dynamics of the transitional flow over a backward-facing step. J. Fluid Mech. 623, 85–119.10.1017/S0022112008005235Google Scholar
Shur, M. L., Spalart, P. R., Strelets, M. K. & Travin, A. K. 2008 A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Intl J. Heat Fluid Flow 29 (6), 1638–1649.10.1016/j.ijheatfluidflow.2008.07.001Google Scholar
Shur, M. L., Spalart, P. R., Strelets, M. K. & Travin, A. K. 2015 An enhanced version of des with rapid transition from RANS to les in separated flows. Flow Turbul. Combust. 95 (4), 709–737.10.1007/s10494-015-9618-0Google Scholar
Spalart, P. R., Deck, S., Shur, M. L., Squires, K. D., Strelets, M. K. & Travin, A. 2006 A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 20 (3), 181–195.10.1007/s00162-006-0015-0Google Scholar
Spalart, P. R., Jou, W. H., Strelets, M. & Allmaras, S. R. 1997 Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. In Advances in DES/LES (ed. Liu, C. & Liu, Z.). Greyden Press.Google Scholar
Speziale, C. G. & Ngo, T. 1988 Numerical solution of turbulent flow past a backward facing step using a nonlinear K-𝜖 model. Intl J Engng Sci. 26 (10), 1099–1112.10.1016/0020-7225(88)90068-7Google Scholar
Thangam, S. & Speziale, C. G. 1992 Turbulent flow past a backward-facing step – a critical evaluation of two-equation models. AIAA J. 30 (5), 1314–1320.10.2514/3.11066Google Scholar
Trias, F. X., Gorobets, A. & Oliva, A. 2015 Turbulent flow around a square cylinder at Reynolds number 22 000: a DNS study. Comput. Fluids 123 (22), 87–98.10.1016/j.compfluid.2015.09.013Google Scholar
Trias, F. X. & Lehmkuhl, O. 2011 A self-adaptive strategy for the time-integration of Navier–Stokes equations. Numer. Heat Transfer B 60 (2), 116–134.10.1080/10407790.2011.594398Google Scholar
Trias, F. X., Soria, M., Oliva, A. & Pérez-Segarra, C. D. 2007 Direct numerical simulations of two- and three-dimensional turbulent natural convection flows in a differentially heated cavity of aspect ratio 4. J. Fluid Mech. 586, 259–293.10.1017/S0022112007006908Google Scholar
Verstappen, R. W. C. P. & Veldman, A. E. P. 2003 Symmetry-preserving discretization of turbulent flow. J. Comput. Phys. 187, 343–368.10.1016/S0021-9991(03)00126-8Google Scholar
Vreman, A. W. & Kuerten, J. G. M. 2014 Comparison of direct numerical simulation databases of turbulent channel flow at Re 𝜏 = 180. Phys. Fluids 26 (1), 1–22.10.1063/1.4861064Google Scholar
Winant, C. D. & Browand, F. K. 1974 Vortex pairing: the mechanism of turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 63 (2), 237–255.10.1017/S0022112074001121Google Scholar