Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dai, Qi
Jin, Tai
Luo, Kun
and
Fan, Jianren
2018.
Direct numerical simulation of particle dispersion in a three-dimensional spatially developing compressible mixing layer.
Physics of Fluids,
Vol. 30,
Issue. 11,
Wang, Jianchun
Wan, Minping
Chen, Song
Xie, Chenyue
and
Chen, Shiyi
2018.
Effect of shock waves on the statistics and scaling in compressible isotropic turbulence.
Physical Review E,
Vol. 97,
Issue. 4,
Dai, Qi
Jin, Tai
Luo, Kun
Xiao, Wei
and
Fan, Jianren
2019.
Direct numerical simulation of a three-dimensional spatially evolving compressible mixing layer laden with particles. II. Turbulence anisotropy and growth rate.
Physics of Fluids,
Vol. 31,
Issue. 8,
Luo, Kun
Dai, Qi
Liu, Xiaofei
and
Fan, Jianren
2019.
Effects of wall roughness on particle dynamics in a spatially developing turbulent boundary layer.
International Journal of Multiphase Flow,
Vol. 111,
Issue. ,
p.
140.
Ren, Zhaoxin
Wang, Bing
Xiang, Gaoming
Zhao, Dan
and
Zheng, Longxi
2019.
Supersonic spray combustion subject to scramjets: Progress and challenges.
Progress in Aerospace Sciences,
Vol. 105,
Issue. ,
p.
40.
Mao, Chaoli
Jin, Tai
Luo, Kun
and
Fan, Jianren
2019.
Investigation of supersonic turbulent flows over a sphere by fully resolved direct numerical simulation.
Physics of Fluids,
Vol. 31,
Issue. 5,
Dai, Qi
Jin, Tai
Luo, Kun
and
Fan, Jianren
2019.
Direct numerical simulation of a three-dimensional spatially evolving compressible mixing layer laden with particles. I. Turbulent structures and asymmetric properties.
Physics of Fluids,
Vol. 31,
Issue. 8,
Wang, Jianchun
Wan, Minping
Chen, Song
Xie, Chenyue
Zheng, Qinmin
Wang, Lian-Ping
and
Chen, Shiyi
2020.
Effect of flow topology on the kinetic energy flux in compressible isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Xiao, Wei
Jin, Tai
Luo, Kun
Dai, Qi
and
Fan, Jianren
2020.
Eulerian–Lagrangian direct numerical simulation of preferential accumulation of inertial particles in a compressible turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Hansson, Kaelan
and
Boyd, Iain D.
2020.
Modeling Requirements for Accurate Prediction of Radiative Transfer in Particle Laden Flow.
Dai, Qi
Luo, Kun
Fan, Jianren
Guo, Zeqing
and
Chen, Zhihua
2021.
Fluctuations of thermodynamic variables in compressible isotropic turbulence laden with inertial particles.
Physics of Fluids,
Vol. 33,
Issue. 9,
Sakurai, Yoshiki
Ishihara, Takashi
Furuya, Hitomi
Umemura, Masayuki
and
Shiraishi, Kenji
2021.
Effects of the Compressibility of Turbulence on the Dust Coagulation Process in Protoplanetary Disks.
The Astrophysical Journal,
Vol. 911,
Issue. 2,
p.
140.
Zhang, Qingqing
and
Xiao, Zuoli
2021.
On the time irreversibility of compressible turbulence reflected by particles of various inertias.
Physics of Fluids,
Vol. 33,
Issue. 3,
Xiao, Hualin
Luo, Kun
Jin, Tai
Wang, Haiou
and
Fan, Jianren
2021.
Direct numerical simulation of turbulence modulation by premixed flames in a model annular swirling combustor.
Proceedings of the Combustion Institute,
Vol. 38,
Issue. 2,
p.
3013.
Wang, Xiangjun
Wan, Minping
and
Biferale, Luca
2022.
Acceleration statistics of tracer and light particles in compressible homogeneous isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 935,
Issue. ,
Kumar, S.
and
Ghosh, S.
2022.
Application of bandwidth-optimized WENO schemes to DNS of shock–turbulence interaction problems.
Shock Waves,
Vol. 32,
Issue. 1,
p.
69.
Dai, Qi
Wang, Xiang
Feng, Wenbin
Zhao, Zijie
Guo, Zeqing
and
Chen, Zhihua
2022.
Direct numerical simulation of turbulence anisotropy and growth rate in the supersonic non-isothermal mixing layer.
Physics of Fluids,
Vol. 34,
Issue. 8,
Jin, Tai
Wang, Gaofeng
Zou, Jianfeng
Shao, Changxiao
Luo, Kun
and
Fan, Jianren
2022.
Multiscale Simulation of Liquid Jet Breakup in Swirling Crossflows: Breakup Mechanism and Spray Structures.
SSRN Electronic Journal ,
Dai, Qi
Zhang, Xin
Yuan, Xin
and
Feng, Wenbin
2022.
Direct numerical simulation of turbulent structures and asymmetric properties in the supersonic non-isothermal mixing layer.
Physics of Fluids,
Vol. 34,
Issue. 12,
Li, Fei
Li, Peibo
Liu, Xu
Wang, Hongbo
Sun, Mingbo
Wang, Zhenguo
Li, Fan
Zhang, Jincheng
and
Yang, Xiaolong
2023.
Numerical study on spray characteristics of liquid jets in supersonic crossflow.
Aerospace Science and Technology,
Vol. 141,
Issue. ,
p.
108543.
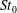 $St_{0}$ ) are conducted while fixing both their volume fraction and particle densities. The underlying physical mechanisms responsible for turbulence modulation are analysed through investigating the particle motion in the different cases and the transport equations of turbulent kinetic energy, vorticity and dilatation, especially the two-way coupling terms. Our results show that microparticles (
$St_{0}$ ) are conducted while fixing both their volume fraction and particle densities. The underlying physical mechanisms responsible for turbulence modulation are analysed through investigating the particle motion in the different cases and the transport equations of turbulent kinetic energy, vorticity and dilatation, especially the two-way coupling terms. Our results show that microparticles ( 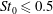 $St_{0}\leqslant 0.5$ ) augment turbulent kinetic energy and the rotational motion of fluid, critical particles (
$St_{0}\leqslant 0.5$ ) augment turbulent kinetic energy and the rotational motion of fluid, critical particles ( 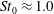 $St_{0}\approx 1.0$ ) enhance the rotational motion of fluid, and large particles (
$St_{0}\approx 1.0$ ) enhance the rotational motion of fluid, and large particles ( 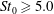 $St_{0}\geqslant 5.0$ ) attenuate turbulent kinetic energy and the rotational motion of fluid. The compressibility of the turbulence field is suppressed for all the cases, and the suppression is more significant if the Stokes number of particles is close to 1. The modifications of turbulent kinetic energy, the rotational motion and the compressibility are all related with the particle inertia and distributions, and the suppression of the compressibility is attributed to the preferential concentration and the inertia of particles.
$St_{0}\geqslant 5.0$ ) attenuate turbulent kinetic energy and the rotational motion of fluid. The compressibility of the turbulence field is suppressed for all the cases, and the suppression is more significant if the Stokes number of particles is close to 1. The modifications of turbulent kinetic energy, the rotational motion and the compressibility are all related with the particle inertia and distributions, and the suppression of the compressibility is attributed to the preferential concentration and the inertia of particles.

