Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-29T08:28:13.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of turbulent scalar transport across a flat surface

Published online by Cambridge University Press:  11 March 2014

H. Herlina  and
J. G. Wissink
H. Herlina*
Affiliation:
Institute for Hydromechanics, Karlsruhe Institute of Technology, Kaiserstr. 12, 76131 Karlsruhe, Germany
J. G. Wissink
Affiliation:
School of Engineering and Design, Brunel University London, Kingston Lane, Uxbridge UB8 3PH, UK
*
†Email address for correspondence: herlina.herlina@kit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

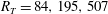To elucidate the physical mechanisms that play a role in the interfacial transfer of atmospheric gases into water, a series of direct numerical simulations of mass transfer across the air–water interface driven by isotropic turbulence diffusing from below has been carried out for various turbulent Reynolds numbers ($R_T=84,195,507$). To allow a direct (unbiased) comparison of the instantaneous effects of scalar diffusivity, in each of the DNS up to six scalar advection–diffusion equations with different Schmidt numbers were solved simultaneously. As far as the authors are aware this is the first simulation that is capable to accurately resolve the realistic Schmidt number, 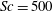$\mathit{Sc}=500$, that is typical for the transport of atmospheric gases such as oxygen in water. For the range of turbulent Reynolds numbers and Schmidt numbers considered, the normalized transfer velocity 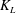$K_L$ was found to scale with 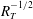$R_T^{-{1/2}}$ and 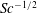$\mathit{Sc}^{-{1/2}}$, which indicates that the largest eddies present in the isotropic turbulent flow introduced at the bottom of the computational domain tend to determine the mass transfer. The 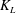$K_L$ results were also found to be in good agreement with the surface divergence model of McCready, Vassiliadou & Hanratty (AIChE J., vol. 32, 1986, pp. 1108–1115) when using a constant of proportionality of 0.525. Although close to the surface large eddies are responsible for the bulk of the gas transfer, it was also observed that for higher 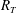$R_T$ the influence of smaller eddies becomes more important.

JFM classification

Geophysical and Geological Flows: Air/sea interactions Mathematical Foundations: Computational methods Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 744 , 10 April 2014 , pp. 217 - 249
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banerjee, S., Lakehal, D. & Fulgosi, M. 2004 Surface divergence model for scalar exchange between turbulent streams. Intl J. Multiphase Flow 30, 963–977.Google Scholar
Banerjee, S., Rhodes, E. & Scott, D. S. 1968 Mass transfer to falling wavy liquid films in turbulent flow. Ind. Engng. Chem. Fundam. 7, 22–27.CrossRefGoogle Scholar
Brumley, B. H. & Jirka, G. H. 1987 Near-surface turbulence in agrid-stirred tank. J. Fluid Mech. 183, 235–263.Google Scholar
Brumley, B. H. & Jirka, G. H. 1988 Air–water transfer of slightly soluble gases: turbulence interfacial processes and conceptual models. Phys. Chem. Hydrodyn. 10 (3), 295–319.Google Scholar
Calmet, I. & Magnaudet, J. 2003 Statistical structure of high-reynolds-number turbulence close to the free surface of an open-channel flow. J. Fluid Mech. 474, 355–378.Google Scholar
Chu, C. R. & Jirka, G. H. 1992 Turbulent gas flux measurements below the air–water interface of a grid-stirred tank. Intl J. Heat Mass Transfer 35 (8), 1957–1968.Google Scholar
Danckwerts, P. V. 1951 Significance of liquid-film coefficients in gas absorption. Ind. Engng. Chem. 43, 1460–1467.Google Scholar
Fortescue, G. E. & Pearson, J. R. 1967 On gas absorption into a turbulent liquid. Chem. Engng Sci. 22, 187–216.Google Scholar
Grötzbach, G. 1983 Spatial resolution requirements for direct numerical simulation of the Rayleigh–Bènard convection. J. Comput. Phys. 49, 241–264.Google Scholar
Handler, R. A., Saylor, J. R., Leighton, R. I. & Rovelstad, A. L. 1999 Transport of a passive scalar at a shear-free boundary in fully turbulent open channel flow. Phys. Fluids 11, 2607–2625.Google Scholar
Hasegawa, Y. & Kasagi, N. 2009 Hybrid DNS/LES of high schmidt number mass transfer across turbulent airwater interface. Intl J. Heat Mass Transfer 52, 1012–1022.CrossRefGoogle Scholar
Herlina,  & Jirka, G. H. 2004 Application of LIF to investigate gas transfer near the air–water interface in a grid-stirred tank. Exp. Fluids 37 (3), 341–349.Google Scholar
Herlina,  & Jirka, G. H. 2008 Experiments on gas transfer at the air–water interface induced by oscillating grid turbulence. J. Fluid Mech. 59, 183–208.Google Scholar
Higbie, R. 1935 The rate of absorption of a pure gas into a still liquid during short periods of exposure. AIChE Trans. 31, 365–390.Google Scholar
Hopfinger, E. J. & Toly, J. A. 1976 Spatially decaying turbulence and its relation to mixing across density interfaces. J. Fluid Mech. 78, 155–175.Google Scholar
Hunt, J. C. R. 1984 Turbulence structure and turbulent diffusion near gas–liquid interfaces. In Gas Transfer at Water Surfaces (ed. Brutsaert, W. & Jirka, G. H.), pp. 67–82. Reidel.Google Scholar
Hunt, J. C. R. & Graham, J. M. R. 1978 Free-stream turbulence near plane boundaries. J. Fluid Mech. 84, 209–235.Google Scholar
Jähne, B. & Haussecker, H. 1998 Air–water gas exchange. Annu. Rev. Fluid Mech. 30, 443–468.Google Scholar
Kermani, A. & Shen, L. 2009 Surface age of surface renewal in turbulent interfacial transport. Geophys. Res. Lett. 36, L10605.Google Scholar
Khakpour, H. R., Shen, L. & Yue, D. K. P. 2011 Transport of passive scalar in turbulent shear flow under a clean or surfactant-contaminated free surface. J. Fluid Mech. 670, 527–557.Google Scholar
Komori, S., Ueda, H., Ogino, F. & Mizushina, T. 1982 Turbulence structure and transport mechanism at the free surface in an open channel flow. Intl J. Heat Mass Transfer 25 (4), 513–521.Google Scholar
Kubrak, B., Herlina, H., Greve, F. & Wissink, J. G. 2013 Low-diffusivity scalar transport using a WENO scheme and dual meshing. J. Comput. Phys. 240, 158–173.Google Scholar
Lamont, J. C. & Scott, D. S. 1970 An eddy cell model of mass transfer into the surface of a turbulent liquid. AIChE J. 16, 513–519.Google Scholar
Lewis, W. K. & Whitman, W. G. 1924 Principles of gas absorption. Indust. Eng. Chem. 16, 1215–1220.Google Scholar
Liu, X., Osher, S. & Chan, T. 1994 Weighted essentially non-oscillatory schemes. J. Comput. Phys. 115, 200–212.Google Scholar
Lu, D. M. & Hetsroni, G. 1995 Direct numerical simulation of a turbulent open channel flow with passive heat transfer. Intl J. Heat Mass Transfer 38, 3241–3251.Google Scholar
Magnaudet, J. & Calmet, I. 2006 Turbulent mass transfer through a flat shear-free surface. J. Fluid Mech. 553, 155–185.Google Scholar
McCready, M. J., Vassiliadou, E. & Hanratty, T. J. 1986 Computer-simulation of turbulent mass-transfer at a mobile interface. AIChE J. 32 (7), 1108–1115.Google Scholar
McKenna, S. P. & McGillis, W. R. 2002 Surface divergence and air–water gas transfer. In Gas Transfer at Water Surfaces (ed. Donelan, M. A., Drennan, W. M., Saltzman, E. S. & Wanninkhof, R.), Geophysical Monograph, vol. 127, pp. 129–134. American Geophysical Union.Google Scholar
McKenna, S. P. & McGillis, W. R. 2004a Observations of flow repeatability and secondary circulation in oscillating grid-stirred tank. Phys. Fluids 16 (9), 3499–3502.Google Scholar
McKenna, S. P. & McGillis, W. R. 2004b The role of free-surface turbulence and surfactants in air–water gas transfer. Int. J. Heat Mass Transfer 47, 539–553.Google Scholar
Moog, D. B. & Jirka, G. H. 2002 Air–water gas transfer in uniform flows with large gravel-bed roughness. In Gas Transfer at Water Surfaces (ed. Donelan, M. A., Drennan, W. M., Saltzman, E. S. & Wanninkhof, R.), Geophysical Monograph, vol 127, pp. 371–376. American Geophysical Union.Google Scholar
Münsterer, T., Mayer, H. J. & Jähne, B.1995 Dual-tracer measurements of concentration profiles in the aqueous mass boundary layer Air–Water Gas Transfer: 3rd International Symposium on Air–Water Gas Transfer, pp. 637–648.Google Scholar
Nagaosa, R. 1999 Direct numerical simulation of vortex structures and turbulent scalar transfer across a free surface in a fully developed turbulence. Phys. Fluids 11, 1581–1595.Google Scholar
O’Connor, D. J. & Dobbins, W. E. 1956 The mechanism of reaeration in natural streams. J. Sanit. Eng. 82 (SA6), 1115–1140.Google Scholar
Plate, E. J. & Friedrich, R. 1984 Reaeration of open channel flow. In Gas Transfer at Air–Water Interfaces (ed. Brutsaert, W. & Jirka, G. H.), pp. 333–346. Reidel.Google Scholar
Pope, S. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Schladow, S. G., Lee, M., Hürzeler, B. E. & Kelly, P. B. 2002 Oxygen transfer across the air–water interface by natural convection in lakes. Limnol. Ocean. 47 (5), 1394–1404.Google Scholar
Sugihara, Y. & Tsumori, H. 2005 Surface-renewal eddies at the air–water interface in oscillating-grid turbulence. In Proceedings of Envirnomental Hydraulics and Sustainable Water Management pp. 199–205. Taylor & Francis.Google Scholar
Tamburrino, A. & Gulliver, J. S. 2002 Free-surface turbulence and mass transfer in a channel flow. AIChE J. 48 (12), 2732–2743.Google Scholar
Theofanous, T. G. 1984 Conceptual models of gas exchange. In Gas Transfer at Air–Water Surfaces pp. 271–281. Reidel.CrossRefGoogle Scholar
Theofanous, T. G., Houze, R. N. & Brumfield, L. K. 1976 Turbulent mass transfer at free, gas liquid interfaces with applications to open channel, bubble and jet flows. Intl J. Heat Mass Transfer 19, 613–624.Google Scholar
Turney, D. E. & Banerjee, S. 2013 Air–water gas transfer and near-surface motions. J. Fluid Mech. 733, 588–624.Google Scholar
Walker, D. T., Leighton, R. I. & Garza-Rios, L. O. 1996 Shear-free turbulence near a flat free surface. J. Fluid Mech. 320, 19–51.Google Scholar
Walker, J. W. & Peirson, W. L. 2008 Measurement of gas transfer across wind-forced wavy airwater interfaces using laser-induced fluorescence. Exp. Fluids 44, 249–259.Google Scholar
Wissink, J. G. 2004 On unconditional conservation of kinetic energy by finite-difference discretisations of the linear and non-linear convection equation. Comput. Fluids 33, 315–343.Google Scholar
Wolff, L. M. & Hanratty, T. J. 1994 Instantaneous concentration profiles of oxygen accompanying absorption in a stratified flow. Exp. Fluids 16, 385–392.Google Scholar
Woodrow, P. T. & Duke, S. R. 2002 LIF measurements of oxygen concentration gradients along flat and wavy air–water interfaces. In Gas Transfer at Water Surfaces (ed. Donelan, M. A., Drennan, W. M., Saltzman, E. S. & Wanninkhof, R.), Geophysical Monograph, vol. 127, pp. 83–88. American Geophysical Union.Google Scholar
Yamamoto, Y., Kunugi, T. & Serizawa, A. 2001 Turbulence statistics and scalar transport in an open-channel flow. J. Turbul. 2, 010.CrossRefGoogle Scholar