Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-11T01:46:01.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulations of local and global torque in Taylor–Couette flow up to Re = 30 000

Published online by Cambridge University Press:  08 February 2013

Hannes J. Brauckmann  and
Bruno Eckhardt
Hannes J. Brauckmann
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, Renthof 6, D-35032 Marburg, Germany
Bruno Eckhardt*
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, Renthof 6, D-35032 Marburg, Germany J.M. Burgerscentrum, Delft University of Technology, Mekelweg 2, 2628 CD Delft, The Netherlands
*
†Email address for correspondence: bruno.eckhardt@physik.uni-marburg.de
Get access Rights & Permissions [Opens in a new window]

Abstract

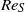The torque in turbulent Taylor–Couette flows for shear Reynolds numbers $R{e}_{S} $ up to 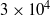$3\times 1{0}^{4} $ at various mean rotations is studied by means of direct numerical simulations for a radius ratio of 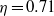$\eta = 0. 71$. Convergence of simulations is tested using three criteria of which the agreement of dissipation values estimated from the torque and from the volume dissipation rate turns out to be most demanding. We evaluate the influence of Taylor vortex heights on the torque for a stationary outer cylinder and select a value of the aspect ratio of 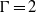$\Gamma = 2$, close to the torque maximum. The local transport resulting in the torque is investigated via the transverse current 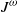${J}^{\omega } $ which measures the transport of angular momentum and can be computed from the velocity field. The typical spatial distribution of the individual convective and viscous contributions to the local torque is analysed for a turbulent flow case. To characterize the turbulent statistics of the transport, probability density functions (p.d.f.s) of local current fluctuations are compared with experimental wall shear stress measurements. P.d.f.s of instantaneous torques reveal a fluctuation enhancement in the outer region for strong counter-rotation. Moreover, we find for simulations realizing the same shear 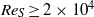$R{e}_{S} \geq 2\times 1{0}^{4} $ the formation of a torque maximum for moderate counter-rotation with angular velocities 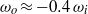${\omega }_{o} \approx - 0. 4\hspace{0.167em} {\omega }_{i} $. In contrast, for 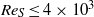$R{e}_{S} \leq 4\times 1{0}^{3} $ the torque features a maximum for a stationary outer cylinder. In addition, the effective torque scaling exponent is shown to also depend on the mean rotation state. Finally, we evaluate a close connection between boundary-layer thicknesses and the torque.

JFM classification

Turbulent Flows: Rotating turbulence Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 718 , 10 March 2013 , pp. 398 - 427
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. J. A. M. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.Google Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.Google Scholar
Bilson, M. & Bremhorst, K. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 579, 227–270.Google Scholar
Boyd, J. P. 2000 Chebyshev and Fourier Spectral Methods, 2nd edn. Dover Publications.Google Scholar
Brown, E. & Ahlers, G. 2007 Temperature gradients, and search for non-Boussinesq effects, in the interior of turbulent Rayleigh–Bénard convection. Europhys. Lett. 80, 14001.Google Scholar
Burin, M. J., Schartman, E. & Ji, H. 2010 Local measurements of turbulent angular momentum transport in circular Couette flow. Exp. Fluids 48, 763–769.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability, 1st edn. Clarendon.Google Scholar
Chossat, P. & Iooss, G. 1994 The Couette–Taylor Problem. Springer.Google Scholar
Coughlin, K. & Marcus, P. S. 1996 Turbulent bursts in Couette–Taylor flow. Phys. Rev. Lett. 77, 2214–2217.Google Scholar
Dong, S. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 587, 373–393.Google Scholar
Dong, S. 2008a Herringbone streaks in Taylor–Couette turbulence. Phys. Rev. E 77, 035301.Google Scholar
Dong, S. 2008b Turbulent flow between counter-rotating concentric cylinders: a direct numerical simulation study. J. Fluid Mech. 615, 371–399.Google Scholar
Dong, S. 2009 Evidence for internal structures of spiral turbulence. Phys. Rev. E 80, 067301.Google Scholar
Dong, S. & Zheng, X. 2011 Direct numerical simulation of spiral turbulence. J. Fluid Mech. 668, 150–173.Google Scholar
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P.-Y., Richard, D. & Zahn, J.-P. 2005 Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17, 095103.Google Scholar
Dubrulle, B. & Hersant, F. 2002 Momentum transport and torque scaling in Taylor–Couette flow from an analogy with turbulent convection. Eur. Phys. J. B 26, 379–386.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007a Fluxes and energy dissipation in thermal convection and shear flows. Europhys. Lett. 78, 24001.Google Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007b Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
Huisman, S. G., van Gils, D. P. M., Grossmann, S., Sun, C. & Lohse, D. 2012 Ultimate turbulent Taylor–Couette flow. Phys. Rev. Lett. 108, 024501.Google Scholar
Jones, C. A. 1985 The transition to wavy Taylor vortices. J. Fluid Mech. 157, 135–162.Google Scholar
Koschmieder, E. L. 1993 Bénard Cells and Taylor Vortices. Cambridge University Press.Google Scholar
Lathrop, D. P., Fineberg, J. & Swinney, H. L. 1992a Transition to shear-driven turbulence in Couette–Taylor flow. Phys. Rev. A 46, 6390–6405.Google Scholar
Lathrop, D. P., Fineberg, J. & Swinney, H. L. 1992b Turbulent flow between concentric rotating cylinders at large Reynolds number. Phys. Rev. Lett. 68, 1515–1518.Google Scholar
Lewis, G. S. & Swinney, H. L. 1999 Velocity structure functions, scaling, and transitions in high-Reynolds-number Couette–Taylor flow. Phys. Rev. E 59, 5457–5467.Google Scholar
Marcus, P. S. 1984 Simulation of Taylor–Couette flow. Part 1. Numerical methods and comparison with experiment. J. Fluid Mech. 146, 45–64.Google Scholar
Meseguer, A., Avila, M., Mellibovsky, F. & Marques, F. 2007 Solenoidal spectral formulations for the computation of secondary flows in cylindrical and annular geometries. Eur. Phys. J. Special Topics 146, 249–259.Google Scholar
Meseguer, A. & Mellibovsky, F. 2007 On a solenoidal Fourier–Chebyshev spectral method for stability analysis of the Hagen–Poiseuille flow. Appl. Numer. Maths 57, 920–938.Google Scholar
Meseguer, A., Mellibovsky, F., Avila, M. & Marques, F. 2009 Instability mechanisms and transition scenarios of spiral turbulence in Taylor–Couette flow. Phys. Rev. E 80, 046315.Google Scholar
Meseguer, A. & Trefethen, L. N. 2003 Linearized pipe flow to Reynolds number $1{0}^{7} $ . J. Comput. Phys. 186, 178–197.Google Scholar
Moser, R. D., Moin, P. & Leonard, A. 1983 A spectral numerical method for the Navier–Stokes equations with applications to Taylor–Couette flow. J. Comput. Phys. 52, 524–544.Google Scholar
Ostilla, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2012 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.Google Scholar
Paoletti, M. S., van Gils, D. P. M., Dubrulle, B., Sun, C., Lohse, D. & Lathrop, D. P. 2012 Angular momentum transport and turbulence in laboratory models of Keplerian flows. Astron. Astrophys. 547 (A64), 1–11.Google Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106, 024501.Google Scholar
Pirrò, D. & Quadrio, M. 2008 Direct numerical simulation of turbulent Taylor–Couette flow. Eur. J. Mech. (B/Fluids) 27, 552–566.Google Scholar
Racina, A. & Kind, M. 2006 Specific power input and local micromixing times in turbulent Taylor–Couette flow. Exp. Fluids 41, 513–522.Google Scholar
Ravelet, F., Delfos, R. & Westerweel, J. 2010 Influence of global rotation and Reynolds number on the large-scale features of a turbulent Taylor–Couette flow. Phys. Fluids 22, 055103.Google Scholar
Recktenwald, A., Lücke, M. & Müller, H. W. 1993 Taylor vortex formation in axial through-flow: linear and weakly nonlinear analysis. Phys. Rev. E 48, 4444–4454.Google Scholar
Riecke, H. & Paap, H.-G. 1986 Stability and wave-vector restriction of axisymmetric Taylor vortex flow. Phys. Rev. A 33, 547–553.Google Scholar
Schartman, E., Ji, H., Burin, M. J. & Goodman, J. 2012 Stability of quasi-Keplerian shear flow in a laboratory experiment. Astron. Astrophys. 543, A94.Google Scholar
Schlichting, H. 1979 Boundary-Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Schumacher, J. & Eckhardt, B. 2004 Fluctuations of energy injection rate in a shear flow. Physica D 187, 370–376.Google Scholar
Smith, G. P. & Townsend, A. A. 1982 Turbulent Couette flow between concentric cylinders at large Taylor numbers. J. Fluid Mech. 123, 187–217.Google Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. Ser. A 223, 289–343.Google Scholar
Taylor, G. I. 1936 Fluid friction between rotating cylinders. I. Torque measurements. Proc. R. Soc. Lond. A 157, 546–564.Google Scholar
Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulent convection in water. Phys. Rev. E 47, R2253.Google Scholar
van Gils, D. P. M., Huisman, S. G., Bruggert, G.-W., Sun, C. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co- and counterrotating cylinders. Phys. Rev. Lett. 106, 024502.Google Scholar
van Gils, D. P. M., Huisman, S. G., Grossmann, S., Sun, C. & Lohse, D. 2012 Optimal Taylor–Couette turbulence. J. Fluid Mech. 706, 118–149.Google Scholar
Wendt, F. 1933 Turbulente Strömungen zwischen zwei rotierenden konaxialen Zylindern. Ing.-Arch. 4, 577–595.Google Scholar
Supplementary material: File

Brauckmann and Eckhardt supplementary data

Supplementary data

Download Brauckmann and Eckhardt supplementary data(File)
File 1.9 KB