Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T03:58:37.445Z Has data issue: false hasContentIssue false
  • English
  • Français

Dissolution of a vertical solid surface by turbulent compositional convection

Published online by Cambridge University Press:  19 January 2015

Ross C. Kerr  and
Craig D. McConnochie
Ross C. Kerr*
Affiliation:
Research School of Earth Sciences, The Australian National University, Canberra, ACT 0200, Australia
Craig D. McConnochie
Affiliation:
Research School of Earth Sciences, The Australian National University, Canberra, ACT 0200, Australia
*
†Email address for correspondence: ross.kerr@anu.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the dissolution of a vertical solid surface in the case where the heat and mass transfer is driven by turbulent compositional convection. A theoretical model of the turbulent dissolution of a vertical wall is developed, which builds on the scaling analysis presented by Kerr (J. Fluid Mech., vol. 280, 1994, pp. 287–302) for the turbulent dissolution of a horizontal floor or roof. The model has no free parameters and no dependence on height. The analysis is tested by comparing it with laboratory measurements of the ablation of a vertical ice wall in contact with salty water. 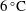The model is found to accurately predict the dissolution velocity for water temperatures up to approximately 5–$6\,^{\circ }\text{C}$, where there is a transition from turbulent dissolution to turbulent melting. We quantify the turbulent convective dissolution of vertical ice bodies in the polar oceans, and compare our results with some field observations.

JFM classification

Phase change: Phase change Phase change: Solidification/melting Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 765 , 25 February 2015 , pp. 211 - 228
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Budd, W. F., Jacka, T. H. & Morgan, V. I. 1980 Antarctic iceberg melt rates derived from size distributions and movement rates. Ann. Glaciol. 1, 103–112.CrossRefGoogle Scholar
Carey, V. P. & Gebhart, B. 1982 Transport near a vertical ice surface melting in saline water: experiments at low salinities. J. Fluid Mech. 117, 403–423.CrossRefGoogle Scholar
Carslaw, H. S. & Jaeger, J. C. 1986 Conduction of Heat in Solids. Oxford University Press.Google Scholar
Diemand, D. 1984 Iceberg temperatures in the North Atlantic – theoretical and measured. Cold Reg. Sci. Technol. 9, 171–178.CrossRefGoogle Scholar
Dutrieux, P., Stewart, C., Jenkins, A., Nicholls, K. W., Corr, H. F. J., Rignot, E. & Steffan, K. 2014 Basal terraces on melting ice shelves. Geophys. Res. Lett. 41, doi:10.1002/2014GL060618.CrossRefGoogle Scholar
Greisman, P. 1979 On upwelling driven by the melt of ice shelves and tidal glaciers. Deep-Sea Res. 26A, 1051–1065.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Holland, P. R., Jenkins, A. & Holland, D. M. 2008 The response of ice shelf basal melting to variations in ocean temperature. J. Clim. 21, 2558–2572.CrossRefGoogle Scholar
Holman, J. P. 2010 Heat Transfer, 10th edn. McGraw-Hill.Google Scholar
Howard, L. N. 1966 Convection at high Reynolds number. In Proceedings of the 11th International Congress of Applied Mechanics, Munich (ed. Görtler, H.), pp. 1109–1115. Springer.Google Scholar
Jenkins, A., Dutrieux, P., Jacobs, S. S., Mcphail, S. D., Perrett, J. R., Webb, A. T. & White, D. 2010 Observations beneath Pine Island Glacier in West Antarctica and implications for its retreat. Nat. Geosci. 3, 468–472.CrossRefGoogle Scholar
Johnson, R. S. & Mollendorf, J. C. 1984 Transport from a vertical ice surface in saline water. Intl J. Heat Mass Transfer 27, 1928–1932.CrossRefGoogle Scholar
Josberger, E. G.1979 Laminar and turbulent boundary layers adjacent to melting vertical ice walls in salt water. PhD thesis, University of Washington, Seattle.Google Scholar
Josberger, E. G. & Martin, S. 1981 A laboratory and theoretical study of the boundary layer adjacent to a vertical melting ice wall in salt water. J. Fluid Mech. 111, 439–473.CrossRefGoogle Scholar
Katsaros, K. B., Liu, W. T., Businger, J. A. & Tillman, J. E. 1977 Heat transport and thermal structure in the interfacial boundary layer measured in an open tank of water in turbulent free convection. J. Fluid Mech. 83, 311–335.CrossRefGoogle Scholar
Kaye, G. W. C. & Laby, T. H. 1973 Tables of Physical and Chemical Constants and some Mathematical Functions. Longman.Google Scholar
Kerr, R. C. 1994a Melting driven by vigorous compositional convection. J. Fluid Mech. 280, 255–285.CrossRefGoogle Scholar
Kerr, R. C. 1994b Dissolving driven by vigorous compositional convection. J. Fluid Mech. 280, 287–302.CrossRefGoogle Scholar
Lick, W. 1965 The instability of a fluid layer with time-dependent heating. J. Fluid Mech. 21, 565–576.CrossRefGoogle Scholar
Macayeal, D. R. 1984 Thermohaline circulation below the Ross Ice Shelf: a consequence of tidally induced vertical mixing and basal melting. J. Geophys. Res. 89, 597–606.CrossRefGoogle Scholar
Neshyba, S. & Josberger, E. G. 1980 On the estimation of Antarctic iceberg melt rate. J. Phys. Oceanogr. 10, 1681–1685.2.0.CO;2>CrossRefGoogle Scholar
Rignot, E. & Jacobs, S. S. 2002 Rapid bottom melting widespread near Antarctic ice sheet grounding lines. Science 296, 2020–2023.CrossRefGoogle ScholarPubMed
Rignot, E., Jacobs, S., Mouginot, J. & Scheuchl, B. 2013 Ice shelf melting around Antarctica. Science 341, 266–270.CrossRefGoogle ScholarPubMed
Rignot, E. & Steffen, K. 2008 Channelized bottom melting and stability of floating ice shelves. Geophys. Res. Lett. 35, L02503.CrossRefGoogle Scholar
Rignot, E., Velicogna, I., Van den Broeke, M. R., Monaghan, A. & Lenaerts, J. 2011 Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise. Geophys. Res. Lett. 38, L05503.CrossRefGoogle Scholar
Russell-Head, D. S. 1980 The melting of free-drifting icebergs. J. Glaciol. 1, 119–121.CrossRefGoogle Scholar
Sharqawy, M. H., Lienhard V, J. H. & Zubair, S. M. 2010 Thermophysical properties of seawater: a review of existing correlations and data. Desalin. Water Treat. 16, 354–380.CrossRefGoogle Scholar
Shepherd, A., Wingham, D. & Rignot, E. 2004 Warm ocean is eroding West Antarctic Ice Sheet. Geophys. Res. Lett. 31, L23402.CrossRefGoogle Scholar
Turner, J. S. 1979 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
UNESCO 1981 Background papers and supporting data on the International Equation of State of Seawater 1980. UNESCO Technical Papers in Marine Science  No. 38.Google Scholar
Vaughan, D. G., Corr, H. F. J., Bindschadler, R. A., Dutrieux, P., Gudmundsson, G. H., Jenkins, A., Newton, T., Vornberger, P. & Wingham, D. J. 2012 Subglacial melt channels and fracture in the floating part of Pine Island Glacier, Antarctica. J. Geophys. Res. 117, F03012.Google Scholar
Vliet, G. C. & Ross, D. C. 1975 Turbulent natural convection on upward and downward facing inclined constant heat flux surfaces. Trans. ASME: J. Heat Transfer 97, 549–555.CrossRefGoogle Scholar
Warner, C. Y. & Arpaci, V. S. 1968 An experimental investigation of turbulent natural convection in air at low pressure along a vertical heated flat plate. Intl J. Heat Mass Transfer 11, 397–406.CrossRefGoogle Scholar
Washburn, E. W.(Ed.) 1926 International Critical Tables of Numerical Data: Physics, Chemistry and Technology. National Academic Press.Google Scholar
Weast, R. C.(Ed.) 1989 CRC Handbook of Chemistry and Physics. CRC Press.Google Scholar
Wells, A. J. & Worster, M. G. 2008 A geophysical-scale model of vertical natural convection boundary layers. J. Fluid Mech. 609, 111–137.CrossRefGoogle Scholar
Wells, A. J. & Worster, M. G. 2011 Melting and dissolving of a vertical solid surface with laminar compositional convection. J. Fluid Mech. 687, 118–140.CrossRefGoogle Scholar
Woods, A. W. 1992 Melting and dissolving. J. Fluid Mech. 239, 429–448.CrossRefGoogle Scholar