Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T15:20:33.721Z Has data issue: false hasContentIssue false
  • English
  • Français

The dominant mechanisms for each regime of secondary flows in horizontal particle-laden pipe flows

Published online by Cambridge University Press:  23 September 2022

Xinchen Zhang Open the ORCID record for Xinchen Zhang [Opens in a new window] ,
Graham J. Nathan Open the ORCID record for Graham J. Nathan [Opens in a new window] ,
Zhao F. Tian Open the ORCID record for Zhao F. Tian [Opens in a new window]  and
Rey C. Chin Open the ORCID record for Rey C. Chin [Opens in a new window]
Xinchen Zhang*
Affiliation:
Centre for Energy Technology, School of Mechanical Engineering, The University of Adelaide, Adelaide, SA 5005, Australia
Graham J. Nathan
Affiliation:
Centre for Energy Technology, School of Mechanical Engineering, The University of Adelaide, Adelaide, SA 5005, Australia
Zhao F. Tian
Affiliation:
Centre for Energy Technology, School of Mechanical Engineering, The University of Adelaide, Adelaide, SA 5005, Australia
Rey C. Chin
Affiliation:
Centre for Energy Technology, School of Mechanical Engineering, The University of Adelaide, Adelaide, SA 5005, Australia
*
†Email address for correspondence: xinchen.zhang01@adelaide.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

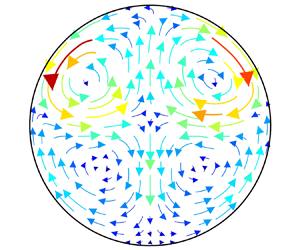
Numerical simulations have been conducted to identify the dominant mechanism responsible for driving secondary flow motions in horizontal particle-laden pipe flows, based on an analysis of the forces acting on each phase. A four-way coupling Euler–Lagrangian approach was employed, using direct numerical simulations for the gas phase and Lagrangian particle tracking to account for the drag, gravitational and lift forces, together with the interactions that occur for both particle–wall and inter-particle collisions. The four different flow regimes, which had been identified previously as depending on various combinations of flow parameters and are characterised by the secondary flow structures of both the fluid and particle phases, were identified via varying the mass loading alone from $\varPhi _m=0.4$ to $\varPhi _m=1.8$. The distribution of the divergence of Reynolds stresses was used to help characterise the classes of the secondary fluid flow. This shows that secondary fluid flows of both the first and second kinds can either exist separately or co-exist in such flows. The forces exerted on the fluid phase by the pressure gradient and fluid–particle interactions were examined qualitatively and quantitatively to identify their contribution to the secondary fluid flow motions. A similar study was also applied to the drag, lift and gravitational forces exerted on the particle phase for the secondary particle flow motions. These were found to explain the secondary flows of both the fluid and particle phases with regard to both the flow direction and magnitude, together with the interaction between the two phases.

JFM classification

Turbulent Flows: Pipe flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 949 , 25 October 2022 , A10
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alletto, M. & Breuer, M. 2013 Prediction of turbulent particle-laden flow in horizontal smooth and rough pipes inducing secondary flow. Intl J. Multiphase Flow 55, 80–98.CrossRefGoogle Scholar
Balachandar, S. 2009 A scaling analysis for point–particle approaches to turbulent multiphase flows. Intl J. Multiphase Flow 35 (9), 801–810.CrossRefGoogle Scholar
Balachandar, S. & Eaton, J.K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.CrossRefGoogle Scholar
Belt, R.J., Daalmans, A. & Portela, L.M. 2012 Experimental study of particle-driven secondary flow in turbulent pipe flows. J. Fluid Mech. 709, 1–36.CrossRefGoogle Scholar
Burton, T.M. & Eaton, J.K. 2005 Fully resolved simulations of particle–turbulence interaction. J. Fluid Mech. 545, 67–111.CrossRefGoogle Scholar
Chin, C., Monty, J.P. & Ooi, A. 2014 Reynolds number effects in DNS of pipe flow and comparison with channels and boundary layers. Intl J. Heat Fluid Flow 45, 33–40.CrossRefGoogle Scholar
Chin, R.C., Vinuesa, R., Örlü, R., Cardesa, J.I., Noorani, A., Chong, M.S. & Schlatter, P. 2020 Backflow events under the effect of secondary flow of Prandtl's first kind. Phys. Rev. Fluids 5 (7), 074606.CrossRefGoogle Scholar
Dykhno, L.A., Williams, L.R. & Hanratty, T.J. 1994 Maps of mean gas velocity for stratified flows with and without atomization. Intl J. Multiphase Flow 20 (4), 691–702.CrossRefGoogle Scholar
Ergun, S. & Orning, A.A. 1949 Fluid flow through randomly packed columns and fluidized beds. Ind. Engng Chem. 41 (6), 1179–1184.CrossRefGoogle Scholar
Fernandes, C., Semyonov, D., Ferrás, L.L. & Nóbrega, J.M. 2018 Validation of the CFD-DPM solver dpmfoam in OpenFOAM through analytical, numerical and experimental comparisons. Granul. Matt. 20 (4), 1–18.CrossRefGoogle Scholar
Flores, A.G., Crowe, K.E. & Griffith, P. 1995 Gas-phase secondary flow in horizontal, stratified and annular two-phase flow. Intl J. Multiphase Flow 21 (2), 207–221.CrossRefGoogle Scholar
Galletti, B. & Bottaro, A. 2004 Large-scale secondary structures in duct flow. J. Fluid Mech. 512, 85–94.CrossRefGoogle Scholar
Geurts, B.J. 2010 Large-eddy simulation of multiscale particle dynamics at high volume concentration in turbulent channel flow. In Multiscale Methods in Computational Mechanics, pp. 95–113. Springer.CrossRefGoogle Scholar
Gidaspow, D. 1994 Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions. Academic Press.Google Scholar
Goldschmidt, M.J.V., Beetstra, R. & Kuipers, J.A.M. 2002 Hydrodynamic modelling of dense gas–fluidised beds: comparison of the kinetic theory of granular flow with 3D hard-sphere discrete particle simulations. Chem. Engng Sci. 57 (11), 2059–2075.CrossRefGoogle Scholar
Hinze, J.O. 1973 Experimental investigation on secondary currents in the turbulent flow through a straight conduit. Appl. Sci. Res. 28 (1), 453–465.CrossRefGoogle Scholar
Kalpakli Vester, A., Örlü, R. & Alfredsson, P.H. 2016 Turbulent flows in curved pipes: recent advances in experiments and simulations. Appl. Mech. Rev. 68 (5), 050802.CrossRefGoogle Scholar
Lain, S. & Sommerfeld, M. 2012 Numerical calculation of pneumatic conveying in horizontal channels and pipes: detailed analysis of conveying behaviour. Intl J. Multiphase Flow 39, 105–120.CrossRefGoogle Scholar
Lain, S., Sommerfeld, M. & Quintero, B. 2009 Numerical simulation of secondary flow in pneumatic conveying of solid particles in a horizontal circular pipe. Braz. J. Chem. Engng 26 (3), 583–594.CrossRefGoogle Scholar
Larsson, I.A.S., Lindmark, E.M., Lundström, T.S. & Nathan, G.J. 2011 Secondary flow in semi-circular ducts. J. Fluids Engng 133 (10), 101206.CrossRefGoogle Scholar
Mei, R. 1992 An approximate expression for the shear lift force on a spherical particle at finite Reynolds number. Intl J. Multiphase Flow 18 (1), 145–147.CrossRefGoogle Scholar
Mei, R. & Klausner, J.F. 1994 Shear lift force on spherical bubbles. Intl J. Heat Fluid Flow 15 (1), 62–65.CrossRefGoogle Scholar
Noorani, A., El Khoury, G.K. & Schlatter, P. 2013 Evolution of turbulence characteristics from straight to curved pipes. Intl J. Heat Fluid Flow 41, 16–26.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Sekimoto, A., Kawahara, G., Sekiyama, K., Uhlmann, M. & Pinelli, A. 2011 Turbulence- and buoyancy-driven secondary flow in a horizontal square duct heated from below. Phys. Fluids 23 (7), 075103.CrossRefGoogle Scholar
Sommerfeld, M. & Lain, S. 2009 From elementary processes to the numerical prediction of industrial particle-laden flows. Multiphase Sci. Technol. 21 (1-2), 123–140.CrossRefGoogle Scholar
Speziale, C.G. 1982 On turbulent secondary flows in pipes of noncircular cross-section. Intl J. Engng Sci. 20 (7), 863–872.CrossRefGoogle Scholar
Tian, R., Wei, M., Dai, X., Song, P. & Shi, L. 2019 Buoyancy effect on the mixed convection flow and heat transfer of supercritical R134a in heated horizontal tubes. Intl J. Heat Mass Transfer 144, 118607.CrossRefGoogle Scholar
Van't Westende, J.M.C., Belt, R.J., Portela, L.M., Mudde, R.F. & Oliemans, R.V.A. 2007 Effect of secondary flow on droplet distribution and deposition in horizontal annular pipe flow. Intl J. Multiphase Flow 33 (1), 67–85.CrossRefGoogle Scholar
Vollestad, P., Angheluta, L. & Jensen, A. 2020 Experimental study of secondary flows above rough and flat interfaces in horizontal gas–liquid pipe flow. Intl J. Multiphase Flow 125, 103235.CrossRefGoogle Scholar
Vreman, A.W. 2015 Turbulence attenuation in particle-laden flow in smooth and rough channels. J. Fluid Mech. 773, 103–136.CrossRefGoogle Scholar
Wang, Z., Örlü, R., Schlatter, P. & Chung, Y.M. 2018 Direct numerical simulation of a turbulent 90$^\circ$ bend pipe flow. Intl J. Heat Fluid Flow 73, 199–208.CrossRefGoogle Scholar
Wen, C.Y. & Yu, Y.H. 1966 A generalized method for predicting the minimum fluidization velocity. AIChE J. 12 (3), 610–612.CrossRefGoogle Scholar
Yao, L.-S. 1978 a Entry flow in a heated straight tube. J. Fluid Mech. 88 (3), 465–483.CrossRefGoogle Scholar
Yao, L.-S. 1978 b Free-forced convection in the entry region of a heated straight pipe. J. Heat Transfer 100 (2), 212–219.CrossRefGoogle Scholar
Zhang, X., Nathan, G.J., Tian, Z.F. & Chin, R.C. 2021 a Flow regimes within horizontal particle-laden pipe flows. Intl J. Multiphase Flow 143, 103748.CrossRefGoogle Scholar
Zhang, X., Nathan, G.J., Tian, Z.F. & Chin, R.C. 2021 b The influence of the coefficient of restitution on flow regimes within horizontal particle-laden pipe flows. Phys. Fluids 33 (12), 123318.CrossRefGoogle Scholar