Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-29T03:47:58.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Downstream decay of fully developed Dean flow

Published online by Cambridge University Press:  15 July 2015

Jesse T. Ault ,
Kevin K. Chen  and
Howard A. Stone
Jesse T. Ault
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Kevin K. Chen
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Howard A. Stone*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: hastone@princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

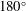Direct numerical simulations were used to investigate the downstream decay of fully developed flow in a $180^{\circ }$ curved pipe that exits into a straight outlet. The flow is studied for a range of Reynolds numbers and pipe-to-curvature radius ratios. Velocity, pressure and vorticity fields are calculated to visualize the downstream decay process. Transition ‘decay’ lengths are calculated using the norm of the velocity perturbation from the Hagen–Poiseuille velocity profile, the wall-averaged shear stress, the integral of the magnitude of the vorticity, and the maximum value of the 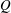$Q$-criterion on a cross-section. Transition lengths to the fully developed Poiseuille distribution are found to have a linear dependence on the Reynolds number with no noticeable dependence on the pipe-to-curvature radius ratio, despite the flow’s dependence on both parameters. This linear dependence of Reynolds number on the transition length is explained by linearizing the Navier–Stokes equations about the Poiseuille flow, using the form of the fully developed Dean flow as an initial condition, and using appropriate scaling arguments. We extend our results by comparing this flow recovery downstream of a curved pipe to the flow recovery in the downstream outlets of a T-junction flow. Specifically, we compare the transition lengths between these flows and document how the transition lengths depend on the Reynolds number.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 777 , 25 August 2015 , pp. 219 - 244
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Aerospace and Mechanical Engineering, USC, Los Angeles, CA 90089, USA.

References

Anwer, M. & So, R. M. C. 1993 Swirling turbulent flow through a curved pipe. Part I: effect of swirl and bend curvature. Exp. Fluids 14, 85–96.Google Scholar
Anwer, M., So, R. M. C. & Lai, Y. G. 1989 Perturbation by and recovery from bend curvature of a fully developed turbulent pipe flow. Phys. Fluids 1, 1387–1397.CrossRefGoogle Scholar
Atkinson, B., Brocklebank, M. P., Card, C. C. H. & Smith, J. M. 1969 Low Reynolds number developing flows. AIChE J. 15, 548–553.CrossRefGoogle Scholar
Austin, L. R. & Seader, J. D. 1973 Fully developed viscous flow in coiled circular pipes. AIChE J. 19, 85–94.CrossRefGoogle Scholar
Berger, S. A. & Talbot, L. 1983 Flow in curved pipes. Annu. Rev. Fluid Mech. 15, 461–512.Google Scholar
Chen, K. K., Rowley, C. W. & Stone, H. A. 2015 Vortex dynamics in a pipe T-junction: recirculation and sensitivity. Phys. Fluids 27 (3), 034107.CrossRefGoogle Scholar
Dean, W. R. 1927 Note on the motion of fluid in a curved pipe. Phil. Mag. 20, 208–223.Google Scholar
Dean, W. R. 1928 The stream-line motion of fluid in a curved pipe. Phil. Mag. 5, 673–695.CrossRefGoogle Scholar
Dennis, S. C. R. & Riley, N. 1991 On the fully developed flow in a curved pipe at large Dean number. Proc. R. Soc. Lond. A 434, 473–478.Google Scholar
Enayet, M. M., Gibson, M. M., Taylor, A. M. K. P. & Yianneskis, M. 1982 Laser-doppler measurements of laminar and turbulent flow in a pipe bend. Intl J. Heat Fluid Flow 3, 213–219.Google Scholar
Fairbank, J. A. & So, R. M. C. 1987 Upstream and downstream influence of pipe curvature on the flow through a bend. Intl J. Heat Fluid Flow 8, 211–217.CrossRefGoogle Scholar
Fox, R. W., Pritchard, P. J. & McDonald, A. T. 2009 Introduction to Fluid Mechanics, 7th edn. John Wiley & Sons.Google Scholar
Hellström, F. & Fuchs, L.2007 Numerical computations of steady and unsteady flow in bended pipes. In 37th AIAA Fluid Dynamics Conference and Exhibit, 25–28 June 2007, Miami, FL.Google Scholar
Hellström, L. H. O., Zlatinov, M. B., Cao, G. & Smits, A. J. 2013 Turbulent pipe flow downstream of a $90^{\circ }$  bend. J. Fluid Mech. 735, R7(1–12).CrossRefGoogle Scholar
Hunt, J. C. R., Wray, A. & Moin, P.1988 Eddies, stream, and convergence zones in turbulent flows. Tech. Rep. CTR-S88. Center for Turbulence Research.Google Scholar
Issa, R. I. 1985 Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65.CrossRefGoogle Scholar
Issa, R. I. 1986 The computation of compressible and incompressible recirculating flows by a non-iterative implicit scheme. J. Comput. Phys. 62, 66–82.CrossRefGoogle Scholar
Kalpakli, A., Örlü, R., Tillmark, N. & Alfredsson, P. H. 2011 Pulsatile turbulent flow through pipe bends at high Dean and Womersley numbers. J. Phys. 318, 092023.Google Scholar
Liu, S. & Masliyah, J. H. 1996 Steady developing laminar flow in helical pipes with finite pitch. Intl J. Comput. Fluid Dyn. 6, 209–224.CrossRefGoogle Scholar
Mohanty, A. K. & Asthana, S. B. L. 1978 Laminar flow in the entrance region of a smooth pipe. J. Fluid Mech. 90, 433–447.Google Scholar
Olson, D. E. & Snyder, B. 1985 The upstream scale of flow development in curved circular pipes. J. Fluid Mech. 150, 139–158.CrossRefGoogle Scholar
Pruvost, J., Legrand, J. & Legentilhomme, P. 2004 Numerical investigation of bend and torus flows. Part I: effect of swirl motion on flow structure in U-bend. Chem. Engng Sci. 59, 3345–3357.CrossRefGoogle Scholar
Sakakibara, J. & Machida, N. 2012 Measurement of turbulent flow upstream and downstream of a circular pipe bend. Phys. Fluids 24, 041702.Google Scholar
Singh, M. P. 1974 Entry flow in a curved pipe. J. Fluid Mech. 65, 517–539.Google Scholar
Smith, F. T. 1976 Fluid flow into a curved pipe. Proc. R. Soc. Lond. A 351, 71–87.Google Scholar
Smits, A. J., Young, S. T. B. & Bradshaw, P. 1979 The effect of short regions of high surface curvature on turbulent boundary layers. J. Fluid Mech. 94, 209–242.CrossRefGoogle Scholar
So, R. M. C. & Anwer, M. 1993 Swirling turbulent flow through a curved pipe. Part II: recovery from swirl and bend curvature. Exp. Fluids 14, 169–177.CrossRefGoogle Scholar
Sudo, K., Sumida, M. & Hibara, H. 2000 Experimental investigation on turbulent flow through a circular-sectioned $180^{\circ }$ bend. Exp. Fluids 28, 51–57.Google Scholar
Tiwari, P., Antal, S. P. & Podowski, M. l.  Z. 2006 Three-dimensional fluid mechanics of particulate two-phase flows in U-bend and helical conduits. Phys. Fluids 18, 043304.Google Scholar
Tunstall, M. J. & Harvey, J. K. 1968 On the effect of a sharp bend in a fully developed turbulent pipe-flow. J. Fluid Mech. 34, 595–608.Google Scholar
Vigolo, D., Radl, S. & Stone, H. A. 2014 Unexpected trapping of particles at a T-junction. Proc. Natl Acad. Sci. USA 111, 4770–4775.Google Scholar
Weller, H. G., Tabor, G., Jasak, H. & Fureby, C. 1998 A tensorial approach to continuum mechanics using object-oriented techniques. Comput. Phys. 12, 620–631.Google Scholar
Winters, K. H. 1987 A bifurcation study of laminar flow in a curved tube of rectangular cross-section. J. Fluid Mech. 180, 343–369.CrossRefGoogle Scholar
Yao, L. S. & Berger, S. A. 1975 Entry flow in a curved pipe. J. Fluid Mech. 67, 177–196.Google Scholar