Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T07:01:47.866Z Has data issue: false hasContentIssue false
  • English
  • Français

The drag-adjoint field of a circular cylinder wake at Reynolds numbers 20, 100 and 500

Published online by Cambridge University Press:  30 July 2013

Qiqi Wang  and
Jun-Hui Gao
Qiqi Wang*
Affiliation:
Department of Aeronautics and Astronautics, MIT, Cambridge, MA 02139, USA
Jun-Hui Gao
Affiliation:
Beihang University, Beijing 100191, China
*
†Email address for correspondence: qiqi@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

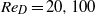This paper analyses the adjoint solution of the Navier–Stokes equation. We focus on flow across a circular cylinder at three Reynolds numbers, ${\mathit{Re}}_{D} = 20, 100$ and 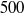$500$. The quantity of interest in the adjoint formulation is the drag on the cylinder. We use classical fluid mechanics approaches to analyse the adjoint solution, which is a vector field similar to a flow field. Production and dissipation of kinetic energy of the adjoint field is discussed. We also derive the evolution of circulation of the adjoint field along a closed material contour. These analytical results are used to explain three numerical solutions of the adjoint equations presented in this paper. The adjoint solution at 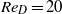${\mathit{Re}}_{D} = 20$, a viscous steady state flow, exhibits a downstream suction and an upstream jet, the opposite of the expected behaviour of a flow field. The adjoint solution at 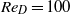${\mathit{Re}}_{D} = 100$, a periodic two-dimensional unsteady flow, exhibits periodic, bean-shaped circulation in the near-wake region. The adjoint solution at 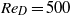${\mathit{Re}}_{D} = 500$, a turbulent three-dimensional unsteady flow, has complex dynamics created by the shear layer in the near wake. The magnitude of the adjoint solution increases exponentially at the rate of the first Lyapunov exponent. These numerical results correlate well with the theoretical analysis presented in this paper.

JFM classification

Nonlinear Dynamical Systems: Chaos Mathematical Foundations: Variational methods Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 730 , 10 September 2013 , pp. 145 - 161
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. & Henderson, R. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Becker, R. & Rannacher, R. 2001 An optimal control approach to a posteriori error estimation in finite element methods. In Acta Numerica (ed. Iserles, A.). Cambridge University Press.Google Scholar
Ham, F., Mattsson, K., Iaccarino, G. & Moin, P. 2007 Towards Time-Stable and Accurate LES on Unstructured Grids. Complex Effects in Large Eddy Simulation, vol. 56, Springer.Google Scholar
Jackson, C. P. 1987 A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 182, 23–45.CrossRefGoogle Scholar
Jameson, A. 1988 Aerodynamic design via control theory. J. Sci. Comput. 3, 233–260.Google Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.Google Scholar
Noack, B. R. & Eckelmann, H. 1994 A global stability analysis of the steady and periodic cylinder wake. J. Fluid Mech. 270, 297–330.CrossRefGoogle Scholar
Pierce, N. & Giles, M. 2000 Adjoint recovery of superconvergent functionals from PDE approximations. SIAM Rev. 42 (2), 247–264.CrossRefGoogle Scholar
Provansal, M, Mathis, C. & Boyer, L. 1987 Bénard–von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.CrossRefGoogle Scholar
Schmid, P. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Wang, Q. 2009 Uncertainty quantification for unsteady fluid flow using adjoint-based approaches. PhD thesis, Stanford University.CrossRefGoogle Scholar
Wang, Q., Moin, P. & Iaccarino, G. 2009 Minimal repetition dynamic checkpointing algorithm for unsteady adjoint calculation. SIAM J. Sci. Comput. 31 (4), 2549–2567.CrossRefGoogle Scholar
Williamson, C. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar