Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-29T07:54:19.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamic reconstruction and data reconstruction for subsampled or irregularly sampled data

Published online by Cambridge University Press:  20 July 2017

Jakub Krol Open the ORCID record for Jakub Krol [Opens in a new window]  and
Andrew Wynn
Jakub Krol
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
Andrew Wynn*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: a.wynn@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The Nyquist–Shannon criterion indicates the sample rate necessary to identify information with particular frequency content from a dynamical system. However, in experimental applications such as the interrogation of a flow field using particle image velocimetry (PIV), it may be impracticable or expensive to obtain data at the desired temporal resolution. To address this problem, we propose a new approach to identify temporal information from undersampled data, using ideas from modal decomposition algorithms such as dynamic mode decomposition (DMD) and optimal mode decomposition (OMD). The novel method takes a vector-valued signal, such as an ensemble of PIV snapshots, sampled at random time instances (but at sub-Nyquist rate) and projects onto a low-order subspace. Subsequently, dynamical characteristics, such as frequencies and growth rates, are approximated by iteratively approximating the flow evolution by a low-order model and solving a certain convex optimisation problem. The methodology is demonstrated on three dynamical systems, a synthetic sinusoid, the cylinder wake at Reynolds number 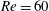$Re=60$ and turbulent flow past the axisymmetric bullet-shaped body. In all cases the algorithm correctly identifies the characteristic frequencies and oscillatory structures present in the flow.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Nonlinear Dynamical Systems: Nonlinear Dynamical Systems
Type
Papers
Information
Journal of Fluid Mechanics , Volume 825 , 25 August 2017 , pp. 133 - 166
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Bagheri, S. 2013 Koopman-mode decomposition of the cylinder wake. J. Fluid Mech. 726, 596–623.CrossRefGoogle Scholar
Candes, E. J. & Tao, T. 2006a Near-optimal signal recovery from random projections: universal encoding strategies? IEEE Trans. Inf. Theory 52, 5406–5425.CrossRefGoogle Scholar
Candes, E. J. & Wakin, M. B. 2008 An introduction to compressive sampling. IEEE Signal Process. Magazine 25 (2), 21–30.CrossRefGoogle Scholar
Candes, R. J., J., E. & Tao, T. 2006b Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 52 (2), 489–509.CrossRefGoogle Scholar
Chen, K. K., Tu, J. H. & Rowley, C. W. 2012 Variants of dynamic mode decomposition: boundary condition, Koopman, and Fourier analyses. J. Nonlinear Sci. 22 (6), 887–915.CrossRefGoogle Scholar
Choi, W. P., Jeon, H. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40 (1), 113–139.CrossRefGoogle Scholar
Donoho, D. L. 2006 Compressed sensing. IEEE Trans. Inf. Theory 52 (4), 1289–1306.CrossRefGoogle Scholar
Elsinga, G. E., Scarano, F., Wieneke, B. & van Oudheusden, B. W. 2006 Tomographic particle image velocimetry. Exp. Fluids 41, 933–947.CrossRefGoogle Scholar
Grandemange, M., Gohlke, M., Parezanović, V. & Cadot, O. 2012 On experimental sensitivity analysis of the turbulent wake from an axisymmetric blunt trailing edge. Phys. Fluids 24, 035106.CrossRefGoogle Scholar
Grilli, M., Schmid, P. J., Hickel, S. & Adams, N. A. 2012 Analysis of unsteady behaviour in shockwave turbulent boundary layer interaction. J. Fluid Mech. 700, 16–28.CrossRefGoogle Scholar
Hemati, M. S., Rowley, C. W. & Nichols, J. W.2017 De-biasing the dynamic mode decomposition for applied Koopman spectral analysis. Theor. Comput. Fluid Dyn. doi:10.1007/s00162-017-0432-2.CrossRefGoogle Scholar
Holmes, P., Lumley, J. L. & Berkooz, G. 1996 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.CrossRefGoogle Scholar
Jovanovic, M. R., Schmid, P. J. & Nichols, J. W. 2014 Sparsity-promoting dynamic mode decomposition. Phys. Fluids 26, 024103.CrossRefGoogle Scholar
Leroux, R. & Cordier, L. 2016 Dynamic mode decomposition for non-uniformly sampled data. Exp. Fluids 57 (5), 94.CrossRefGoogle Scholar
Lu, L. & Papadakis, G. 2011 Investigation of the effect of external periodic flow pulsation on a cylinder wake using linear stability analysis. Phys. Fluids 23, 094105.CrossRefGoogle Scholar
Lu, L. & Papadakis, G. 2014 An iterative method for the computation of the response of linearised Navier–Stokes equations to harmonic forcing and application to forced cylinder wakes. Intl J. Numer. Meth. Fluids 74, 794–817.CrossRefGoogle Scholar
Muld, T. W., Efraimsson, G. & Henningson, D. S. 2012 Flow structures around a high-speed train extracted using proper orthogonal decomposition and dynamic mode decomposition. Comput. Fluids 57, 87–97.CrossRefGoogle Scholar
Needell, D. & Tropp, J. A. 2009 Cosamp: iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 26, 301–321.CrossRefGoogle Scholar
Noack, B. R., Afanasiev, K., Morzynski, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.CrossRefGoogle Scholar
Nyquist, H. 1928 Certain topics in telegraph transmission theory. Proc. IEEE 90 (2), 280–305.CrossRefGoogle Scholar
Orlandi, P. 1994 On the generation of turbulent wall friction. Phys. Fluids 6, 634–641.CrossRefGoogle Scholar
Oxlade, A. R., Morrison, J. F., Qubain, A. & Rigas, G. 2015 High-frequency forcing of a turbulent axisymmetric wake. J. Fluid Mech. 770, 305–318.CrossRefGoogle Scholar
Proctor, J. L., Brunton, S. L. & Kutz, J. N.2014 Dynamic mode decomposition with control.Google Scholar
Rigas, G., Oxlade, A. R., Morgans, A. S. & Morrison, J. F. 2014 Low-dimensional dynamics of a turbulent axisymmetric wake. J. Fluid Mech. 755, R5.CrossRefGoogle Scholar
Rowley, C. W., Mezic, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.CrossRefGoogle Scholar
Sayadi, T., Schmid, P. J., Nichols, J. W. & Moin, P. 2014 Reduced-order representation of near-wall structures in the late transitional boundary layer. J. Fluid Mech. 748, 278–301.CrossRefGoogle Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.CrossRefGoogle Scholar
Schmid, P. J., Violato, D. & Scarano, F. 2012 Decomposition of time-resolved tomographic piv. Exp. Fluids 52, 1567–1579.CrossRefGoogle Scholar
Seena, A. & Sung, H. J. 2011 Dynamic mode decomposition of turbulent cavity flows for self-sustained oscillations. Intl J. Heat Fluid Flow 32, 1098–1110.CrossRefGoogle Scholar
Semeraro, O., Bellani, G. & Lundell, F. 2012 Analysis of time-resolved piv measurements of a confined turbulent jet using POD and Koopman modes. Exp. Fluids 53, 1203–1220.CrossRefGoogle Scholar
Sevilla, A. & Martínez-Bazán, C. 2004 Vortex shedding in high reynolds number axisymmetric bluff-body wakes: local linear instability and global bleed control. Phys. Fluids 16, 3460–3469.CrossRefGoogle Scholar
Tissot, G., Cordier, L., Benard, N. & Noack, B. R. 2014 Model reduction using dynamic mode decomposition. C. R. Méc 342 (67), 410–416.CrossRefGoogle Scholar
Tropp, J. A. & Gilbert, A. C. 2007 Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 53, 4655–4666.CrossRefGoogle Scholar
Tu, J. H., Rowley, C. W., Kutz, J. N. & Shang, J. K. 2014 Spectral analysis of fluid flows using sub-Nyquist-rate PIV data. Exp. Fluids 55, 1805.CrossRefGoogle Scholar
Vinha, N., Meseguer-Garrido, F., De Vicente, J. & Valero, E. 2016 A dynamic mode decomposition of the saturation process in the open cavity flow. Aerosp. Sci. Technol. 52, 198–206.CrossRefGoogle Scholar
Williams, G. 2011 Linear Algebra with Applications. Jones and Bartlett Publishers.Google Scholar
Williams, M. O., Kevrekidis, I. G. & Rowley, C. W. 2015 A datadriven approximation of the Koopman operator: extending dynamic mode decomposition. J. Nonlinear Sci. 25, 1307–1346.CrossRefGoogle Scholar
Wynn, A., Pearson, D. S., Ganapathisubramani, B. & Goulart, P. J. 2013 Optimal mode decomposition for unsteady flows. J. Fluid Mech. 733, 473–503.CrossRefGoogle Scholar