Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T01:36:40.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical interactions between the coherent motion and small scales in a cylinder wake

Published online by Cambridge University Press:  15 May 2014

F. Thiesset ,
L. Danaila  and
R. A. Antonia
F. Thiesset
Affiliation:
CORIA, Avenue de l’Université, BP 12, 76801 Saint Etienne du Rouvray, France School of Engineering, University of Newcastle, NSW 2308, Australia
L. Danaila*
Affiliation:
CORIA, Avenue de l’Université, BP 12, 76801 Saint Etienne du Rouvray, France
R. A. Antonia
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
*
†Email address for correspondence: danaila@coria.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Most turbulent flows are characterized by coherent motion (CM), whose dynamics reflect the initial and boundary conditions of the flow and are more predictable than that of the random motion (RM). The major question we address here is the dynamical interaction between the CM and the RM, at a given scale, in a flow where the CM exhibits a strong periodicity and can therefore be readily distinguished from the RM. The question is relevant at any Reynolds number, but is of capital importance at finite Reynolds numbers, for which a clear separation between the largest and the smallest scales may not exist. Both analytical and experimental tools are used to address this issue. First, phase-averaged structure functions are defined and further used to condition the RM kinetic energy at a scale $r$ on the phase 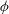$\phi $ of the CM. This tool allows the dependence of the RM to be followed as a function of the CM dynamics. Scale-by-scale energy budget equations are established on the basis of phase-averaged structure functions. They reveal that energy transfer at a scale $r$ is sensitive to an additional forcing mechanism due to the CM. Second, these concepts are tested using hot-wire measurements in a cylinder wake, in which the CM is characterized by a well-defined periodicity. Because the interaction between large and small scales is most likely enhanced at moderate/low Reynolds numbers, and is also likely to depend on the amplitude of the CM, we choose to test our findings against experimental data at 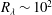$R_{\lambda } \sim 10^2$ and for downstream distances in the range 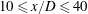$10 \leq x/D \leq 40$. The effects of an increasing Reynolds number are also discussed. It is shown that: (i) a simple analytical expression describes the second-order structure functions of the purely CM. The energy of the CM is not associated with any single scale; instead, its energy is distributed over a range of scales. (ii) Close to the obstacle, the influence of the CM is perceptible even at the smallest scales, the energy of which is enhanced when the coherent strain is maximum. Further downstream from the cylinder, the CM clearly affects the largest scales, but the smallest scales are not likely to depend explicitly on the CM. (iii) The isotropic formulation of the RM energy budget compares favourably with experimental results.

JFM classification

Turbulent Flows: Turbulence theory Vortex Flows: Vortex interactions Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 749 , 25 June 2014 , pp. 201 - 226
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aivalis, K. G., Sreenivasan, K. R., Tsuji, Y., Klewicki, J. C. & Biltoft, C. A. 2002 Temperature structure functions for air flow over moderately heated ground. Phys. Fluids 14, 2439–2446.Google Scholar
Antonia, R. A. & Burattini, P. 2006 Approach to the 4/5 law in homogeneous isotropic turbulence. J. Fluid Mech. 550, 175–184.Google Scholar
Antonia, R. A., Ould-Rouis, M., Anselmet, F. & Zhu, Y. 1997 Analogy between predictions of Kolmogorov and Yaglom. J. Fluid Mech. 332, 395–409.Google Scholar
Antonia, R. A., Smalley, R. J., Zhou, T., Anselmet, F. & Danaila, L. 2003 Similarity of energy structure functions in decaying homogeneous isotropic turbulence. J. Fluid Mech. 487, 245–269.Google Scholar
Antonia, R. A., Zhou, T. & Romano, G. P. 2002 Small-scale turbulence characteristics of two-dimensional bluff body wakes. J. Fluid Mech. 459, 67–92.Google Scholar
Bisset, D. K., Antonia, R. A. & Browne, L. W. B. 1990 Spatial organization of large structures in the turbulent far wake of a cylinder. J. Fluid Mech. 218, 439–461.Google Scholar
Blum, D. B., Bewley, G. P., Bodenschatz, E., Gibert, M., Gylfason, A., Mydlarski, L., Voth, G. A., Xu, H. & Yeung, P. K. 2011 Signatures of non-universal large scales in conditional structure functions from various turbulent flows. New J. Phys. 13, 113020.Google Scholar
Blum, D. B., Kunwar, S. B., Johnson, J. & Voth, G. A. 2010 Effects of nonuniversal large scales on conditional structure functions in turbulence. Phys. Fluids 22, 015107.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.Google Scholar
Brown, G. & Roshko, A. 2012 Turbulent shear layers and wakes. J. Turbul. 13, 1–32.Google Scholar
Cambon, C., Danaila, L., Godeferd, F. S. & Scott, J. F. 2013 Third-order statistics and the dynamics of strongly anisotropic turbulent flows. J. Turbul. 14 (3), 121–160.Google Scholar
Cambon, C. & Gréa, B. -J. 2013 The role of directionality on the structure and dynamics of strongly anisotropic turbulent flows. J. Turbul. 14 (1), 50–71.Google Scholar
Danaila, L., Anselmet, F. & Antonia, R. A. 2002 An overview of the effect of large scale inhomogeneities on small-scale turbulence. Phys. Fluids 14, 2475–2484.CrossRefGoogle Scholar
Danaila, L., Anselmet, F. & Zhou, T. 2004 Turbulent energy scale-budget equations for nearly homogeneous sheared turbulence. Flow Turbul. Combust. 72, 287–310.Google Scholar
Danaila, L., Antonia, R. A. & Burattini, P. 2012a Comparison between kinetic energy and passive scalar energy transfer in locally homogeneous isotropic turbulence. Physica D 241, 224–231.Google Scholar
Danaila, L., Krawczynski, J. F., Thiesset, F. & Renou, B. 2012b Yaglom-like equation in axisymmetric anisotropic context. Physica D 241, 216–223.Google Scholar
Davidson, P. A. & Pearson, B. R. 2005 Identifying turbulent energy distributions in real, rather than Fourier, space. Phys. Rev. Lett. 95, 214501.Google Scholar
Domaradzki, J. A., Metcalfe, R. W., Rogallo, R. S. & Riley, J. J. 1987 Analysis of subgrid-scale eddy viscosity with use of results from direct numerical simulations. Phys. Rev. Lett. 58 (6), 547–550.Google Scholar
Hill, R. J. 2001 Equations relating structure functions of all orders. J. Fluid Mech. 434, 379–388.Google Scholar
Hosokawa, I. 2007 A paradox concerning the refined similarity hypothesis of Kolmogorov for isotropic turbulence. Prog. Theor. Phys. 118, 169–173.Google Scholar
Kang, H. S. & Meneveau, C. 2002 Universality of large eddy simulation model parameters across a turbulent wake behind a he ated cylinder. J. Turbul. 3, 1–27.CrossRefGoogle Scholar
Kholmyansky, M. & Tsinober, A. 2008 Kolmogorov 4/5 law, nonlocality, and sweeping decorrelation hypothesis. Phys. Fluids 20, 041704.Google Scholar
Kiya, M. & Matsumura, M. 1988 Incoherent turbulence structure in the near wake of a normal plate. J. Fluid Mech. 190, 343–356.Google Scholar
Kolmogorov, A. 1941a Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 125, 15–17.Google Scholar
Kolmogorov, A. 1941b The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. USSR Acad. Sci. 30, 299–303.Google Scholar
Kurien, S. & Sreenivasan, K. R. 2000 Anisotropic scaling contributions to high-order structure functions in high-Reynolds-number turbulence. Phys. Rev. E 62, 2206–2212.Google Scholar
Lin, C. & Hsieh, S. C. 2003 Convection velocity of vortex structures in the near wake of a circular cylinder. J. Engng Mech. 129, 1108–1118.Google Scholar
Marati, N., Casciola, C. M. & Piva, R. 2004 Energy cascade and spatial fluxes in wall turbulence. J. Fluid Mech. 521, 191–215.Google Scholar
Matsumura, M. & Antonia, R. A. 1993 Momentum and heat transport in the turbulent intermediate wake of a circular cylinder. J. Fluid Mech. 250, 651–668.Google Scholar
Monin, A. S. & Yaglom, A. M. 2007 Statistical Fluid Dynamics (ed. Lumley, J. L.), vol. 2. MIT Press.Google Scholar
Mouri, H. & Hori, A. 2010 Two-point velocity average of turbulence: statistics and their implications. Phys. Fluids 22, 115110.Google Scholar
Nichols-Pagel, G. A., Percival, D. B., Reinhall, P. G. & Riley, J. J. 2008 Should structure functions be used to estimate power laws in turbulence? A comparative study. Physica D 237 (5), 665–677.Google Scholar
O’Neil, J. & Meneveau, C. 1997 Subgrid-scale stresses and their modelling in a turbulent plane wake. J. Fluid Mech. 349, 253–293.Google Scholar
Perrin, R., Braza, M., Cid, E., Cazin, S., Barthet, A., Sevrain, A., Mockett, C. & Thiele, F. 2007 Obtaining phase averaged turbulence properties in the near wake of a circular cylinder at high Reynolds number using POD. Exp. Fluids 43, 341–355.Google Scholar
Praskovsky, A. A., Gledzer, E., Karyakin, M. Y. & Zhou, Y. 1993 The sweeping decorrelation hypothesis and energy-inertial range interaction in high Reynolds number flow. J. Fluid Mech. 248, 493–511.Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organised wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54, 263–288.Google Scholar
Roshko, A.1954 On the development of turbulent wakes from vortex streets. Tech. Rep. NACA TR.Google Scholar
Shen, X. & Warhaft, Z. 2000 The anisotropy of the small scale structure in high Reynolds number ( $R_{\lambda }=1000$ ) turbulent shear flow. Phys. Fluids 12, 2976–2989.Google Scholar
Sjögren, T. & Johansson, A. V. 1998 Measurement and modelling of homogeneous axisymmetric turbulence. J. Fluid Mech. 374, 59–90.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Sreenivasan, K. R. & Dhruva, B. 1998 Is there a scaling in high Reynolds-number turbulence?. Prog. Theor. Phys. 130, 103–120.CrossRefGoogle Scholar
Tchoufag, J., Sagaut, P. & Cambon, C. 2012 Spectral approach to finite reynolds number effects on Kolmogorov’s 4/5 law in isotropic turbulence. Phys. Fluids 24, 015107.Google Scholar
Tennekes, H. 1975 Eulerian and Lagrangian time microscales in isotropic turbulence. J. Fluid Mech. 67, 561–567.Google Scholar
Thiesset, F., Antonia, R. A. & Danaila, L. 2013a Scale-by-scale turbulent energy budget in the intermediate wake of two-dimensional generators. Phys. Fluids 25 (11), 115105.Google Scholar
Thiesset, F., Danaila, L. & Antonia, R. A. 2013b Dynamical effect of the total strain induced by the coherent motion on local isotropy in a wake. J. Fluid Mech. 720, 393–423.Google Scholar
Thiesset, F., Danaila, L., Antonia, R. A. & Zhou, T. 2011 Scale-by-scale energy budgets which account for the coherent motion. J. Phys. Conf. Ser. 318, 052040.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flows. Cambridge University Press.Google Scholar
Valente, P.2013 Energy transfer and dissipation in equilibrium and nonequilibrium turbulence. PhD thesis, Imperial College.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Yaglom, A. M. 1949 On the local structure of a temperature field in a turbulent flow. Dokl. Akad. Nauk SSSR 69, 743.Google Scholar
Zhou, Y. & Antonia, R. A. 1992 Convection velocity measurements in a cylinder wake. Exp. Fluids 13, 63–70.Google Scholar
Zhou, Y. & Antonia, R. A. 1993 A study of turbulent vortices in the near wake of a cylinder. J. Fluid Mech. 253, 643–661.Google Scholar
Zhou, Y. & Antonia, R. A. 1995 Memory effects in a turbulent plane wake. Exp. Fluids 19, 112–120.Google Scholar
Zhou, T., Zhou, Y., Yiu, M. W. & Chua, L. P. 2003 Three-dimensional vorticity in a turbulent cylinder wake. Exp. Fluids 35, 459–471.Google Scholar